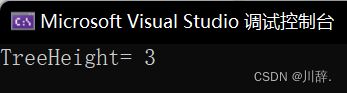数据结构--二链式树(链式)
目录
前言
一.链式二叉树
1.结构特征
2.建立简单二叉树
3. 二叉树的遍历
(1)二叉树三种遍历的结果
(2)前序遍历(先根遍历)
(3)中序遍历
(4)后序遍历
(5)基本原理过程(以先序遍历为例)
二.应用链式二叉树处理问题
1.求二叉树中节点总数
(1)第一种写法
(2)第二种写法(简洁)
2.求叶子节点的个数
3.求二叉树的高度
4.求第k层的节点个数
前言
在学习二叉树的基本操作前,需先要创建一棵二叉树,然后才能学习其相关的基本操作。由于现在大家对二叉树结构掌握还不够深入,为了降低大家学习成本,此处手动快速创建一棵简单的二叉树,快速进入二叉树操作学习,等二叉树结构了解的差不多时,我们反过头再来研究二叉树真正的创建方式。
一.链式二叉树
1.结构特征
typedef int BTDataType;
typedef struct BinaryTreeNode
{
BTDataType data;
struct BinaryTreeNode* left;//左子树
struct BinaryTreeNode* right;//右子树
}TreeNode;2.建立简单二叉树
TreeNode* BuyTreeNode(int x)
{
TreeNode*node = (TreeNode*)malloc(sizeof(TreeNode));
assert(node);
node->data = x;
node->left = NULL;
node->right = NULL;
}
TreeNode* CreatTree()
{
TreeNode* node1 = BuyTreeNode(1);
assert(node1);
TreeNode* node2 = BuyTreeNode(2);
assert(node2);
TreeNode* node3 = BuyTreeNode(3);
assert(node3);
TreeNode* node4 = BuyTreeNode(4);
assert(node4);
TreeNode* node5 = BuyTreeNode(5);
assert(node5);
TreeNode* node6 = BuyTreeNode(6);
assert(node6);
node1->left = node2;
node1->right = node4;
node2->left = node3;
node4->left = node5;
node4->right = node6;
return node1;
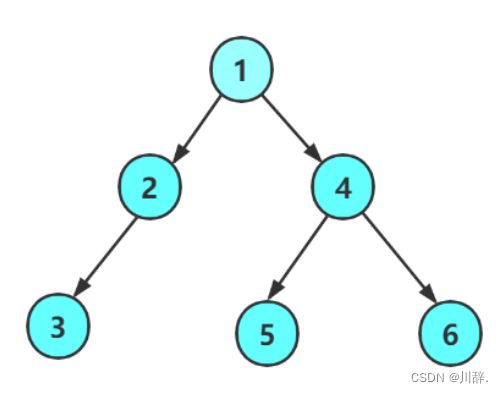
}- 示例
3. 二叉树的遍历
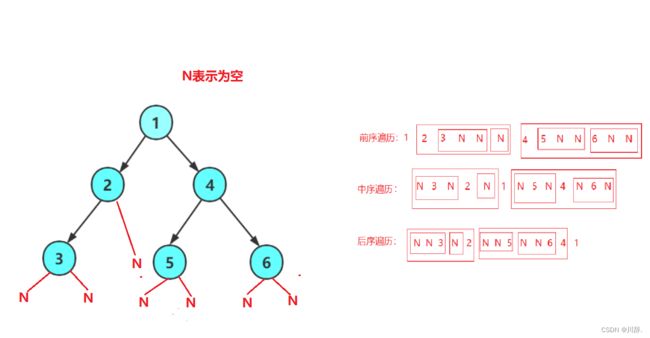
(1)二叉树三种遍历的结果
(2)前序遍历(先根遍历)
- 介绍
前序遍历(先序遍历)——访问根结点的操作发生在遍历其左右子树之前。
(根节点-左子树-右子树)
void PrevOrder(TreeNode* root)
{
if (root == NULL)
{
printf("N ");
return;
}
printf("%d ", root->data);
PrevOrder(root->left);
PrevOrder(root->right);
}结果显示:
(3)中序遍历
- 介绍
中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中(间)。
(左子树-根节点-右子树)
void InOrder(TreeNode* root)
{
if (root == NULL)
{
printf("N ");
return;
}
InOrder(root->left);
printf("%d ", root->data);
InOrder(root->right);
}结果显示:
(4)后序遍历
- 介绍
后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。
(左子树-右子树-根节点)
void PostOrder(TreeNode* root)
{
if (root == NULL)
{
printf("N ");
return;
}
PostOrder(root->left);
PostOrder(root->right);
printf("%d ", root->data);
}结果显示:
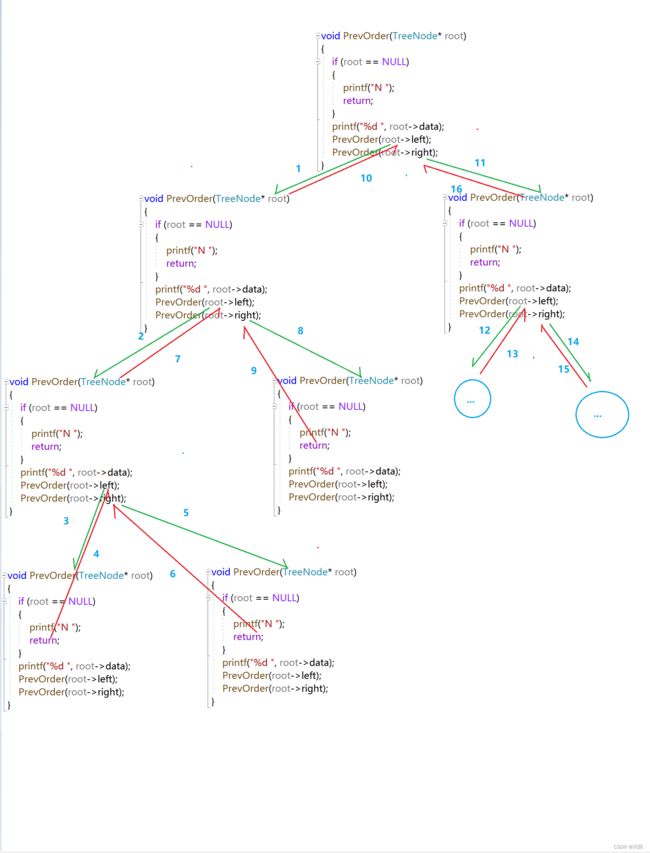
(5)基本原理过程(以先序遍历为例)
二.应用链式二叉树处理问题
1.求二叉树中节点总数
(1)第一种写法
int size=0;//这里size为全局变量
int TreeSize(TreeNode* root)
{
if (root == NULL)
{
return 0;
}
++size;
TreeSize(root->left);
TreeSize(root->right);
return size;
}
int main()
{
TreeNode* root = CreatTree();
size = 0;
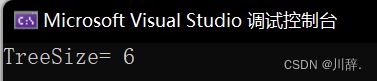
printf("TreeSize= %d\n", TreeSize(root));
size = 0;
printf("TreeSize= %d\n", TreeSize(root));
size = 0;
printf("TreeSize= %d\n", TreeSize(root));
return 0;
}结果:
(2)第二种写法(简洁)
int TreeSize(TreeNode* root)
{
if (root == NULL)
{
return 0;
}
return TreeSize(root->left)+TreeSize(root->right)+1;
}
int main()
{
printf("TreeSize= %d\n", TreeSize(root));
return 0;
}结果:
2.求叶子节点的个数
分治:左子树叶子数+右子树叶子数
返回条件控制:
(1)根节点为空,返回0
(2)根节点不为空,且不存在左右子树(该节点为叶子节点),返回1
(3)递归遍历左右子树
int TreeLeafSize(TreeNode* root)
{
if (root == NULL)
return 0;
if (!root->left && !root->right)
return 1;
return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}
int main()
{
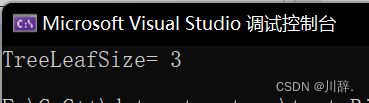
printf("TreeLeafSize= %d\n", TreeLeafSize(root));
return 0;
}结果:
3.求二叉树的高度
分治:
(1)根为空,返回0
(2)根不为空,返回左右子树高度较大的那一个 + 1
int TreeHeight(TreeNode* root)
{
if (root == NULL)
return 0;
int LeftHeight = TreeHeight(root->left);
int RightHeight = TreeHeight(root->right);
return LeftHeight >= RightHeight ? LeftHeight + 1 : RightHeight + 1;
}
int main()
{
printf("TreeHeight= %d\n", TreeHeight(root));
return 0;
}结果:
- 效果不好的代码
int TreeHeight(TreeNode* root)
{
return root == NULL ?0 :
TreeHeight(root->left) > TreeHeight(root->right) ?
TreeHeight(root->left)+1 : TreeHeight(root->right) + 1;
}4.求第k层的节点个数
分治:
(1)为空,返回0
(2)不为空但k=1,返回1
(3) 不为空且k!=1,返回 左子树的第k-1层+右子树的第k-1层
int TreeLevelK(TreeNode* root,int k)
{
assert(k > 0);
if (root == NULL)
return 0;
if ( k == 1)
return 1;
return TreeLevelK(root->left, k - 1) + TreeLevelK(root->right, k - 1);
}
int main()
{
printf("TreeLevelK=%d\n", TreeLevelK(root,3));
return 0;
}