LeetCode 42 接雨水
题目描述
接雨水
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
示例 1:
输入:height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出:6
解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
示例 2:
输入:height = [4,2,0,3,2,5]
输出:9
提示:
n == height.length1 <= n <= 2 * 1040 <= height[i] <= 105
解法
解法1:动态规划
对于下标 i,下雨后水能到达的最大高度等于下标 i 两边的最大高度的最小值。
下标 i 处能接的雨水量等于下标 i 处的水能到达的最大高度减去 height[i]。
使用动态规划找到下标 i 两边的最大高度。
java代码:
class Solution {
public int trap(int[] height) {
int n = height.length;
if (n <= 2) {
return 0;
}
// 先找左边的最大值
int[] leftMax = new int[n];
leftMax[0] = height[0];
for (int i = 1; i < n; ++i) {
leftMax[i] = Math.max(leftMax[i-1], height[i]);
}
// 再找右边的最大值
int[] rightMax = new int[n];
rightMax[n-1] = height[n-1];
for (int i = n -2; i >= 0; --i) {
rightMax[i] = Math.max(height[i], rightMax[i + 1]);
}
// 计算每个单元能存储的水量
int res = 0;
for (int i = 0; i < n; ++i) {
res += Math.min(leftMax[i], rightMax[i]) - height[i];
}
return res;
}
}
复杂度
- 时间复杂度:
O(n),其中 n 为数组的长度 - 空间复杂度:
O(n)。
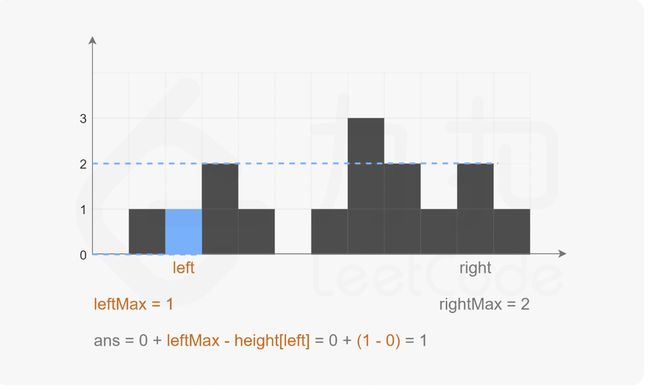
解法2:双指针
分别使用leftMax左指针表示从左边遍历,目前为止的最大值,rightMax右指针表示从右边遍历,目前为止的最大值。
如果 leftMax < rightMax,那么左边遍历到的当前柱子,左边的最大值可以确认了,但是它的右边最大值还没有遍历完,无法确认。但是我们再想想,右边虽然还不知道最大值,但是我们知道了右边当前的最大值,所以可以说,左边遍历到的当前柱子,右边的最大值最小也是rightMax。又由于leftMax < rightMax,当前柱子盛的水是由左右两边最大值的最小值决定的,所以我们已经可以计算出当前柱子的盛水量了,即:
当前柱子的盛水量 = min(leftMax , rightMax) - 当前柱子高度
同理leftMax > rightMax。
java代码:
class Solution {
public int trap(int[] height) {
int left = 0;
int right = height.length -1;
int leftMax = 0;
int rightMax = 0;
int res = 0;
while (left < right) {
leftMax = Math.max(leftMax, height[left]);
rightMax = Math.max(rightMax, height[right]);
if (leftMax < rightMax) {
res += leftMax - height[left];
left ++;
} else {
res += rightMax - height[right];
right --;
}
}
return res;
}
}
复杂度
- 时间复杂度:
O(n),两个指针的移动总次数不超过 n。 - 空间复杂度:
O(1)。
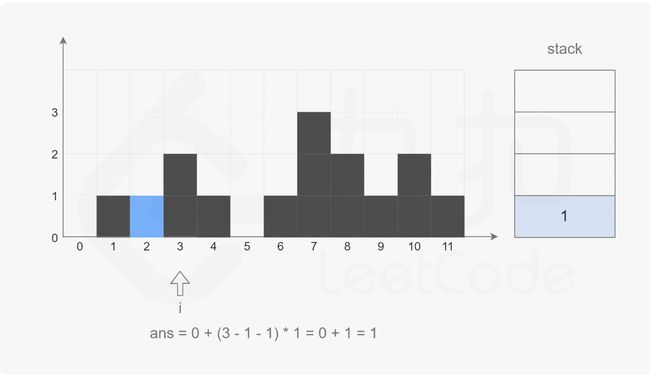
解法3:单调栈
什么是单调栈:栈内的元素是单调的,依次将元素压入栈,如果当前元素小于等于栈顶元素则入栈,如果大于栈顶元素则先将栈顶不断出栈,直到当前元素小于或等于栈顶元素为止,然后再将当前元素入栈。
思路:
依次从左到右遍历柱子高度
- 如果当前柱子高度比前一个小,或栈是空的,则当前数字的下标入栈
- 如果当前柱子高度比前一个大,说明前一个柱子的两边都比它高,形成了"洼地",可以接到雨水了。此时,计算栈顶元素水的高度,弹出栈,继续向前找是否还有比当前柱子小的,依次计算,知道栈为空或者在栈里找到比当前柱子大伙相等的
java代码:
class Solution {
public int trap(int[] height) {
int left = 0;
int right = height.length -1;
int leftMax = 0;
int rightMax = 0;
int res = 0;
while (left < right) {
leftMax = Math.max(leftMax, height[left]);
rightMax = Math.max(rightMax, height[right]);
if (leftMax < rightMax) {
res += leftMax - height[left];
left ++;
} else {
res += rightMax - height[right];
right --;
}
}
return res;
}
}
复杂度
- 时间复杂度:
O(n),两个指针的移动总次数不超过 n。 - 空间复杂度:
O(n)。