深度学习笔试题(一)
一、单选题(1-20题)
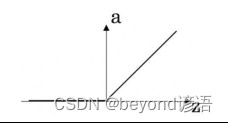
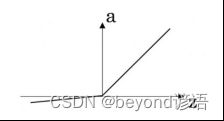
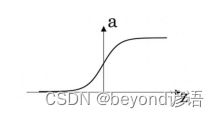
1、这些图中的哪一个表示sigmoid激活函数?(C)
2、对于隐藏单元,tanh激活通常比sigmoid激活函数更有效,因为其输出的平均值接近于1,因此它可以更好地将数据集中到下一层。B
A.对
B.不对
tanh输出在[-1,1],均值为0,可以起到归一化的作用
3. 以下哪个选项正确? C
A、卷积神经网络有反馈连接。
B、增加多层感知机的隐层层数,测试集的分类错误会减小。 不一定,有可能过拟合
C、卷积神经网络会发生权重共享。
D、穷举搜索不可以用来更新参数。
4、正规方程是y,假设您有m=18个训练示例,有n=5个特性(不包括需要另外添加的恒为1的截距项)。对于给定m和n的值,这个方程中,y的维数分别是多少?B
A. 18×5, y 18×1, 5×5
B. 18×6, y 18×1, 6×1
C. 18×5, y 18×1, 5×1
D. 18×6, y 18×6, 6×6
5、假设您有一个数据集,每个示例有m=1000000个示例和n=200000个特性。你想用多元线性回归来拟合参数到我们的数据。你更应该用梯度下降还是正规方程? A
A. 梯度下降,因为正规方程中中计算非常慢
B. 梯度下降,因为它总是收敛到最优
C. 正规方程,因为它提供了一种直接求解的有效方法
D. 正规方程,因为梯度下降可能无法找到最优
6、输入图片为300x300,经过卷积(kernel size 8x8 ,padding 1,stride 2)pooling(kernel size 5x5 ,padding 0,stride 1)之后,输出特征图大小为: C
A.142
B.143
C.144
D.145
卷积层:(300-8+2*1)/2 + 1=148
池化层:(148-5)/1+1=144
7、下面属于无监督学习的是: A
A.K-means
B.决策树
C.SVM
D.F-RCNN
8、假设你的输入的维度为128x128x16,单个1x1的卷积过滤器含有多少个参数(包括偏差)?C
A.1
B.2
C.17
D.4097
9、你有一个64x64x16的输入,并使用步幅为2、过滤器大小为2的最大化池,请问输出是多少?C
A.31x31x16
B.32x32x8
C.32x32x16
D.64x64x8
10、你有一个16x16x8的输入,并使用“pad = 2”进行填充,填充后的尺寸是多少?B
A.18x18x10
B.20x20x8
C.20x20x12
D.18x18x8
11、为什么要对输入x进行归一化?B
A.让参数初始化更快
B.让代价函数更快地优化
C.更容易做数据可视化
D.是另一种正则化——有助减少方差
12、下面哪个选项中哪一项不属于确定性算法?A
A、PCA
B、K-Means
C、以上都不是
确定性算法我的理解是:输入一样,输出也一样
K-Means聚类算法多次训练得到结果不一样
PCA的话,本质在于对一个方差最大化问题的求解,求最优解,必然是确定且唯一
13、当你增大正则化的超参数时会发生什么?B
A.重量变大(远离0)
B.权重变小(接近0)
C.2倍的导致2倍的权重
每次迭代,梯度下降采取更大的步距(与成正比)
14、如果你有10,000个例子,你会如何划分训练/开发/测试集?C
A.33%训练,33%开发,33%测试
B.60%训练,20%开发,20%测试
C.98%训练,1%开发,1%测试
15、开发和测试集应该:A
A.来自同一分布
B.选择随机分布
C.完全相同(一样的(x, y)对)
D.数据数量应该相同
16、你正在训练一个RNN网络,下列选项中,哪一个是最有可能导致你的权重与激活值都是“NaN”的?A
A.梯度爆炸
B.梯度消失
C.ReLU函数作为激活函数g(.),在计算g(z)时,z的数值过大了
D.Sigmoid函数作为激活函数g(.),在计算g(z)时,z的数值过大了
17、对数损失度量函数不可以取负值:B loss常用正值,不代表只能用正值
A.对
B.错
18、下面哪一项对梯度下降(GD)和随机梯度下降(SGD)的描述是正确的? 1 在 GD 中,每一次迭代需要使用整个训练集或子训练集的数据更新一个参数。 2 在 GD 和SGD 中,每一次迭代都需要遍历训练集中的所有样本以更新一次参数。 3 在 GD 和 SGD 中,每一次迭代中都是更新一组参数以最小化损失函数。B
A.只有 1
B.只有 3
C.只有2和3
D.都正确
19、LSTM与GRU的一个主要区别在于GRU将LSTM的哪几个gate融合了? A
a .forget gate b. input gate
c. output gate d. reset gate
A.ab
B.abc
C.abcd
D.bcd
GRU将LSTM中的输入门input gate和遗忘门forget gate进行了合并,称之为更新门
20、以下是目标变量在训练集上的13个实际值[0,0,0,0,1,1,1,1,1,1,1,1,1],目标变量的熵是多少; A
A.-(9/13log(9/13)+4/13log(4/13))
B. 9/13log(9/13)-4/13log(4/13)
C. 9/13log(9/13)+4/13log(4/13)
D. -9/13log(9/13)+4/13log(4/13)
二、多选题(21-30题)
21、以下哪些操作防止过拟合?(选出所有正确项)ABCG
A.交叉验证
B.增加训练数据
C.Dropout
D.L3正则化 没听过,不了解
E.Xavier初始化
F.梯度爆炸
G.L2正则化
22、将参数keep_prob增大但都不超过1会导致以下情况(选出所有正确项):BDF
A.正则化效应被增强
B.正则化效应被减弱
C.模型结构复杂的层取大的keep_prob
D.模型结构复杂的层取小的keep_prob
E.训练集的误差会增加
F.训练集的误差会减小
Keep_prob越大,保留越多的神经元节点,模型会更复杂,能够更好的拟合训练集数据
正则化引入了惩罚项,来防止模型过于复杂,keep_prob越大会导致正则化效应越弱
23、怎么解决神经网络方差较高的问题?B
A.特征工程
B.获取更多测试数据
C.增加每个隐藏层的神经元数量
D.提前终止
E.用更深的神经网络
24、你正在为苹果,香蕉和橘子制作分类器。 假设您的分类器在训练集上有0.5%的错误,以及开发集上有7%的错误。 以下哪项尝试是有希望改善你的分类器的分类效果的?AC
A.增大正则化参数
B.减小正则化参数
C.获取更多训练数据
D.用更大的神经网络
25、以下哪些是“超参数”?(选出所有正确项) CDEF
A.隐藏层规模
B.神经网络的层数
C.正则化参数
D.学习的回合数
E.学习率
F.迭代次数
G.神经元的激活函数
26、假设在一个深度学习网络中,批量梯度下降花费了大量时间时来找到一组参数值,使成本函数小。以下哪些方法可以帮助找到值较小的参数值? BCDE
A.令所有权重值初始化为0
B.尝试调整学习率
C.尝试mini-batch梯度下降
D.尝试对权重进行更好的随机初始化
E.尝试使用 Adam 算法
27、为什么最好的mini-batch的大小通常不是1也不是m,而是介于两者之间? BC
A.如果mini-batch的大小是1,那么在你取得进展前,你需要遍历整个训练集
B.如果mini-batch的大小是m,就会变成批量梯度下降。在你取得进展前,你需要遍历整个训练集
C.如果mini-batch的大小是1,那么你将失去mini-batch将数据矢量化带来的的好处
D.如果mini-batch的大小是m,就会变成随机梯度下降,而这样做经常会比mini-batch慢
28、关于参数共享的下列哪个陈述是正确的?(选出所有正确项)BDE
A.它减少了参数的总数,从而减少过拟合。
B.它允许在整个输入值的多个位置使用特征检测器。
C.它允许为一项任务学习的参数即使对于不同的任务也可以共享(迁移学习)。
D.它允许梯度下降将许多参数设置为零,从而使得连接稀疏。
E.减少模型复杂度。
F.降低模型性能。
29、对于分类问题,我们可以采用哪些损失函数? BD
A.均方误差损失函数
B.交叉熵损失函数
C.平均绝对误差损失函数。
D.二元交叉熵损失函数。
E.Huber Loss。
30、批归一化算法的优点 AE
A.渐少梯度消失
B.减少收敛速度
C.降低训练精度
D.导致过拟合
E.减少人为选择参数