每周一算法：数独游戏

题目链接

数独游戏

题目描述

数独是根据 $9\times 9$ 盘面上的已知数字，推理出所有剩余空格的数字，并满足每一行、每一列、每一个粗线宫内的数字均含 $1-9$ ，不重复。每一道合格的数独谜题都有且仅有唯一答案，推理方法也以此为基础，任何无解或多解的题目都是不合格的。

芬兰一位数学家号称设计出全球最难的“数独游戏”，并刊登在报纸上，让大家去挑战。

这位数学家说，他相信只有“智慧最顶尖”的人才有可能破解这个“数独之谜”。

据介绍，目前数独游戏的难度的等级有一到五级，一是入门等级，五则比较难。不过这位数学家说，他所设计的数独游戏难度等级是十一，可以说是所以数独游戏中，难度最高的等级。他还表示，他目前还没遇到解不出来的数独游戏，因此他认为“最具挑战性”的数独游戏并没有出现。

输入格式

一个未填的数独。

输出格式

填好的数独。

样例 #1

样例输入 #1

8 0 0 0 0 0 0 0 0 
0 0 3 6 0 0 0 0 0 
0 7 0 0 9 0 2 0 0 
0 5 0 0 0 7 0 0 0 
0 0 0 0 4 5 7 0 0 
0 0 0 1 0 0 0 3 0 
0 0 1 0 0 0 0 6 8 
0 0 8 5 0 0 0 1 0 
0 9 0 0 0 0 4 0 0

样例输出 #1

8 1 2 7 5 3 6 4 9 
9 4 3 6 8 2 1 7 5 
6 7 5 4 9 1 2 8 3 
1 5 4 2 3 7 8 9 6 
3 6 9 8 4 5 7 2 1 
2 8 7 1 6 9 5 3 4 
5 2 1 9 7 4 3 6 8 
4 3 8 5 2 6 9 1 7 
7 9 6 3 1 8 4 5 2

样例输入 #2

9 0 0 8 0 0 0 0 0
0 0 0 0 0 0 5 0 0 
0 0 0 0 0 0 0 0 0 
0 2 0 0 1 0 0 0 3
0 1 0 0 0 0 0 6 0
0 0 0 4 0 0 0 7 0
7 0 8 6 0 0 0 0 0 
0 0 0 0 3 0 1 0 0 
4 0 0 0 0 0 2 0 0 

样例输出 #2

9 7 2 8 5 3 6 1 4 
1 4 6 2 7 9 5 3 8 
5 8 3 1 4 6 7 2 9 
6 2 4 7 1 8 9 5 3 
8 1 7 3 9 5 4 6 2 
3 5 9 4 6 2 8 7 1 
7 9 8 6 2 1 3 4 5 
2 6 5 9 3 4 1 8 7 
4 3 1 5 8 7 2 9 6 

算法思想

数独游戏是根据 $9\times 9$ 盘面上的已知数字，推理出所有剩余空格的数字，问题规模很小，直接暴力搜索就可以了。

优化搜索顺序

要进行搜索，首先要确定搜索顺序。当然可以选择任意一个未填数的空格开始搜索，但考虑到搜索效率，应优先搜索可选数字少的空格开始搜索。举个例子：

如下图所示，红色格子中$1,3,4,5,6,7,9$，绿色格子中可选的数字有$2,3,8,9$，应优先搜索绿色格子。

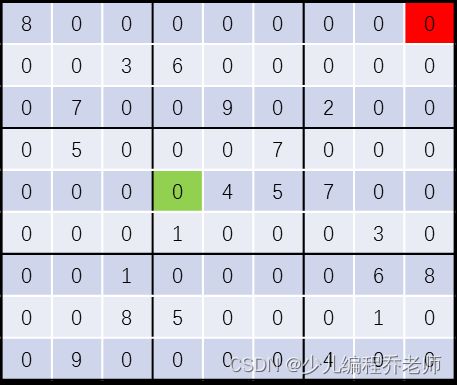
可行性剪枝

通过盘面上确定数字，可以判断当前空格所填的数字是否可行，如果存在冲突，则终止在该分支上的搜索，这就是可行性剪枝。

数独游戏的可行性有$3$个要求：

• 每一行的数字含 $1-9$ ，不重复
• 每一列的数字含 $1-9$ ，不重复
• 每一个粗线宫内数字含 $1-9$ ，不重复

那么如何快速得到在$x$行$y$列的空格中可行的数字有哪些呢？这里可以借助状态压缩的思想，用一个整数的二进制形式$(000000000{)}_2\sim (111111111{)}_2$来标记哪些数字是可行的，如下图所示，可选数字为$2,3,8,9$

对于每行、每列和每个$3\times 3$的小九宫格都可以设置一个状态：

• $\text{row}(x)$表示在$x$行可选数字的状态
• $\text{col}(y)$表示在$y$列可选数字的状态
• $\text{cell}(\lfloor \frac{x}{3}\rfloor ,\lfloor \frac{y}{3}\rfloor )$表示$(x,y)$所在的小九宫格可选数字的状态

这三者同时满足就是在$x$行$y$列可选数字的状态，可以通过对三者进行按位与运算获得，即row[x] & col[y] & cell[x/3][y/3]。

二进制枚举

当确定了可选数字的状态，不妨设为$\text{state}$，如何快速枚举其中可选的数字呢？可以通过$\text{lowbit}$方法实现，$$\text{lowbit(x) = x\&-x}$$

$\text{lowbit}$运算返回整数二进制形式中最低位的$1$和它后面的0组成的数字，该数字为$2$的正整数次幂。例如：

• $\text{state}=(110000110{)}_2$，$\text{lowbit(state)}=(10{)}_2=2$
• $\text{state}=(110000100{)}_2$，$\text{lowbit(state)}=(100{)}_2=4$

通过$\text{lowbit}$方法就可以快速枚举$\text{state}$中可选的数字。

代码实现

#include 
using namespace std;
const int N = 9, M = 1 << N;
int g[N][N];
int row[N], col[N], cell[3][3];
int ones[M]; //获取所有二进制形式中1的个数
int log[M]; //获取log(n)
//预处理每行每列每个小九宫格可选数字的状态
void init() 
{
    for(int i = 0; i < 9; i ++)
        row[i] = col[i] = (1 << 9) - 1;
    for(int i = 0; i < 3; i ++)
        for(int j = 0; j < 3; j ++)
            cell[i][j] = (1 << 9) - 1;
}
void fill(int x, int y, int t, bool is_set)
{
    int s = 1 << (t - 1); //要改变的状态，状态从0开始，所以要减1
    if(is_set) //填数
    {
        g[x][y] = t;
        //填完数，该数的状态设为不可行
        row[x] -= s, col[y] -= s, cell[x/3][y/3] -= s; 
    }
    else //清空
    {
        g[x][y] = 0;
        //清空后，该数的状态设为可行
        row[x] += s, col[y] += s, cell[x/3][y/3] += s;
    }
}
//获取x行y列可选数字的状态
int get(int x, int y)
{
    return row[x] & col[y] & cell[x/3][y/3];
}
int lowbit(int x)  // 返回末尾的1
{
    return x & -x;
}

bool dfs(int cnt)
{
    if(cnt == 0) return true; //全部填完
    //优化搜索顺序，寻找可选数字最少的行列
    int minv = 10, x, y;
    for(int i = 0; i < 9; i ++)
        for(int j = 0; j < 9; j ++)
        {
            if(g[i][j] == 0)
            {
                int state = get(i, j);
                if(ones[state] < minv)
                {
                    minv = ones[state], x = i, y = j;
                }
            }
        }
    //从x行y列开始搜索
    int state = get(x, y); //从x行y列可选数字的状态
    for(int i = state; i != 0; i -= lowbit(i))
    {
        int t = log[lowbit(i)] + 1; //获取对应要填的数1~9，log中映射的是0~8，所以要+1
        fill(x, y, t, true);
        if(dfs(cnt - 1)) return true;
        fill(x, y, t, false); //回溯，恢复现场
    }
    return false;
}
int main()
{
    init();
    //统计每个状态中1的个数
    for(int i = 0; i < 1 << 9; i ++)
        for(int j = 0; j < 9; j ++)
            ones[i] += i >> j & 1; 
    //预处理log(i)，方便快速获取要填的数字，注意预处理的是0~8
    for(int i = 0; i < 9; i ++) log[1 << i] = i;
    
    int cnt = 0; //一共要填cnt个数
    for(int i = 0; i < 9; i ++)
        for(int j = 0; j < 9; j ++)
        {
            cin >> g[i][j];
            if(g[i][j] != 0) //数字已填
                fill(i, j, g[i][j], true); //填数
            else cnt ++;
        }
    
    //暴力搜索，一共要填cnt个数
    dfs(cnt);
    
    //输出结果
    for(int i = 0; i < 9; i ++)
    {
        for(int j = 0; j < 9; j ++)
            cout << g[i][j] << " ";
        cout << endl;
    }
}