【机器学习理论】人工神经网络之神经元的MP模型
神经元的MP模型
- 1 神经元的生理结构
- 2 神经元的数学模型
-
- 2.1 从生理结构到MP模型的构建过程
- 2.2 MP模型的直观图示
- 2.3 MP模型的标准形式
- 2.4 MP模型的向量形式
- 2.5 小结
- 3 MP模型的加权求和的数学意义
- 4 总结
人工神经网络是人工智能仿生学派的一大创造,人工神经网络的诞生极大地受到人体内的真实的神经元的生理结构的启发,并且最初的神经元的数学模型就是仿照真实的神经元的结构来设计的,所以在介绍神经元的MP模型之前,先看看生物学上的神经元的生理结构。
1 神经元的生理结构
2 神经元的数学模型
1943年,心理学家W·S·McCulloch和数理逻辑学家W·pitts基于神经元的生理结构,建立了单个神经元的数学模型,当时他们提出的模型叫做MP模型,MP模型是一种简单的神经元数学模型。
2.1 从生理结构到MP模型的构建过程
假设一个人体神经元有 m m m 个树突,每个树突可以接受 1 1 1 个电刺激信号,一共接受 m m m 个电刺激信号。那么现在来建立MP模型。
- 将人体神经元接受的 m m m 个外部刺激模拟为 m m m 个输入信号 x i ( i = 1 , 2 , . . . , m ) x_i(i=1,2,...,m) xi(i=1,2,...,m)
- 将每个树突对外部刺激的加工过程模拟为以某个权重 ω i ( i = 1 , 2 , . . . , m ) \omega_i(i=1,2,...,m) ωi(i=1,2,...,m) 对其对应的输入信号 x i ( i = 1 , 2 , . . . , m ) x_i(i=1,2,...,m) xi(i=1,2,...,m) 进行加权(两者相乘),即 w i x i ( i = 1 , 2 , . . . , m ) w_ix_i(i=1,2,...,m) wixi(i=1,2,...,m)
- 将细胞核的加工过程模拟为对加权后的输入信号进行求和,再加上一个偏置 b b b,即 ∑ i = 1 m ω i x i + b \sum_{i=1}^m\omega_ix_i+b ∑i=1mωixi+b
- 最后将轴突模拟为对加权求和的结果进行非线性变换,即 ϕ ( ∑ i = 1 m ω i x i + b ) \phi(\sum_{i=1}^m\omega_ix_i+b) ϕ(∑i=1mωixi+b), ϕ ( ∗ ) \phi(*) ϕ(∗) 是一个激活函数
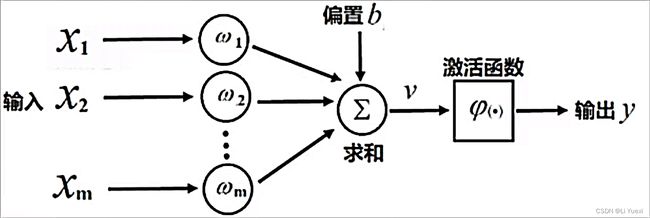
2.2 MP模型的直观图示
2.3 MP模型的标准形式
单个神经元的MP模型如下所示:
y = ϕ ( ∑ i = 1 m ω i x i + b ) ( 2.1 ) y = \phi(\sum_{i=1}^m\omega_ix_i+b) \quad\quad\quad\quad\quad\quad(2.1) y=ϕ(i=1∑mωixi+b)(2.1)
其中,
x i ( i = 1 , 2 , . . . , m ) x_i(i=1,2,...,m) xi(i=1,2,...,m) 表示第 i i i 个输入变量(自变量)
m m m 表示输入变量的个数
ω i ( i = 1 , 2 , . . . , m ) \omega_i(i=1,2,...,m) ωi(i=1,2,...,m) 表示第 i i i 个权重,与相同下标的 x i x_i xi 相对应
b b b 表示偏置
y y y 表示输出变量(因变量)
ϕ \phi ϕ 表示一个激活函数,它对线性加权求和的结果进行非线性变换
如果将多个神经元的MP模型统一编号,可以表示成一个式子:
y k = ϕ ( ∑ i = 1 m ω k i x i + b k ) ( 2.2 ) y_k = \phi(\sum_{i=1}^m\omega_{ki} x_i+b_k) \quad\quad\quad\quad\quad\quad(2.2) yk=ϕ(i=1∑mωkixi+bk)(2.2)
其中,
y k ( k = 1 , 2 , . . . , n y_k(k=1,2,...,n yk(k=1,2,...,n) 表示第 k k k 个神经元的输出变量
ω k i ( k = 1 , 2 , . . . , n ; i = 1 , 2 , . . . , m ) \omega_{ki}(k=1,2,...,n;i=1,2,...,m) ωki(k=1,2,...,n;i=1,2,...,m) 表示第 k k k 个神经元的第 i i i 个权重
b k ( k = 1 , 2 , . . . , n ) b_k(k=1,2,...,n) bk(k=1,2,...,n) 表示第 k k k 个神经元的偏置
n n n 表示神经元的个数
2.4 MP模型的向量形式
可以采用向量的形式表示MP模型
设 W = ( ω 1 , ω 2 , . . . , ω m ) T W=(\omega_1,\omega_2,...,\omega_m)^T W=(ω1,ω2,...,ωm)T, X = ( x 1 , x 2 , . . . , x m ) T X=(x_1,x_2,...,x_m)^T X=(x1,x2,...,xm)T
则MP模型可以表示成:
y = ϕ ( W T X + b ) ( 2.3 ) y = \phi(W^TX+b) \quad\quad\quad\quad\quad\quad(2.3) y=ϕ(WTX+b)(2.3)
同理,多个神经元的MP模型的向量形式:
设 W k = ( ω k 1 , ω k 2 , . . . , ω k m ) T ( k = 1 , 2 , . . . , n ) W_k=(\omega_{k1},\omega_{k2},...,\omega_{km})^T(k=1,2,...,n) Wk=(ωk1,ωk2,...,ωkm)T(k=1,2,...,n), X = ( x 1 , x 2 , . . . , x m ) T X=(x_1,x_2,...,x_m)^T X=(x1,x2,...,xm)T
则
y k = ϕ ( W k T X + b k ) ( 2.4 ) y_k = \phi(W_k^TX+b_k) \quad\quad\quad\quad\quad\quad(2.4) yk=ϕ(WkTX+bk)(2.4)
2.5 小结
MP模型在一定程度上反映了神经元对外界刺激的一种响应,但是在生物学上,并没有明确的证据能证明这种加权求和再非线性变换的模型能完全真实反映实际的神经元运作机制。不过无论怎样,MP模型在数学上是正确的,在它基础上提出的感知器算法,对解决一些简单的实际的机器学习问题,也很有帮助。
3 MP模型的加权求和的数学意义
为什么模型中会有加权求和的部分呢?因为加权求和是对模型函数的一阶泰勒近似。
证明:
设神经元的输出 y y y 是输入 x 1 , x 2 , x 3 , . . . , x m x_1,x_2,x_3,...,x_m x1,x2,x3,...,xm 的函数,即
y = f ( x 1 , x 2 , . . . , x m ) ( 3.1 ) y = f(x_1,x_2,...,x_m) \quad\quad\quad\quad\quad\quad(3.1) y=f(x1,x2,...,xm)(3.1)
由 m m m 元函数的泰勒级数(更确切地说,麦克劳林级数),可得
f ( x 1 , x 2 , . . . , x m ) = f ( 0 , 0 , . . . , 0 ) + ∑ i = 1 m [ ∂ f ∂ x i ∣ ( 0 , 0 , . . . , 0 ) ] x i + ⋅ ⋅ ⋅ f(x_1,x_2,...,x_m) =f(0,0,...,0)+\sum_{i=1}^m[\frac{ \partial f }{ \partial x_i }|(0,0,...,0)]x_i+··· f(x1,x2,...,xm)=f(0,0,...,0)+i=1∑m[∂xi∂f∣(0,0,...,0)]xi+⋅⋅⋅
令 b = f ( 0 , 0 , . . . , 0 ) b=f(0,0,...,0) b=f(0,0,...,0), ω i = ∂ f ∂ x i ∣ ( 0 , 0 , . . . , 0 ) ( i = 1 , 2 , . . . , m ) \omega_i=\frac{ \partial f }{ \partial x_i }|(0,0,...,0)(i=1,2,...,m) ωi=∂xi∂f∣(0,0,...,0)(i=1,2,...,m),则
f ( x 1 , x 2 , . . . , x m ) = ∑ i = 1 m ω i x i + b + ⋅ ⋅ ⋅ ( 3.2 ) f(x_1,x_2,...,x_m)=\sum_{i=1}^m\omega_ix_i+b + ···\quad\quad\quad\quad(3.2) f(x1,x2,...,xm)=i=1∑mωixi+b+⋅⋅⋅(3.2)
容易看出, ∑ i = 1 m ω i x i + b \sum_{i=1}^m\omega_ix_i+b ∑i=1mωixi+b 是对 f ( x 1 , x 2 , . . . , x m ) f(x_1,x_2,...,x_m) f(x1,x2,...,xm) 的一阶泰勒近似,后面还有无穷多个高阶项。
最后,再找到一个非线性激活函数 ϕ ( ∗ ) \phi(*) ϕ(∗) ,施加到 ∑ i = 1 m ω i x i + b \sum_{i=1}^m\omega_ix_i+b ∑i=1mωixi+b 上,即
f ( x 1 , x 2 , . . . , x m ) = ϕ ( ∑ i = 1 m ω i x i + b ) ( 3.3 ) f(x_1,x_2,...,x_m) = \phi(\sum_{i=1}^m\omega_ix_i+b)\quad\quad\quad\quad\quad(3.3) f(x1,x2,...,xm)=ϕ(i=1∑mωixi+b)(3.3)
这使得 f ( x 1 , x 2 , . . . , x m ) f(x_1,x_2,...,x_m) f(x1,x2,...,xm) 可以精确表示大量非线性函数。
4 总结
MP模型不能反映神经元的真实作用机制,目前最常用的人工神经网络和深度学习的基本结构单元仍然是MP模型的神经元。
一些研究者提出更加复杂的神经元模型,并开发了一些神经网络算法,例如,基于神经元集聚和释放电荷机制的脉冲神经网络(Spiking Neural Network,SNN),又如基于神经元的反馈机制的霍普菲尔德神经网络(Hopfield Neural Network,HNN)。
这些复杂的神经元模型在影响力和应用广泛程度上,远远不如MP模型。既然我们对真实的神经元机制还不够清楚,无论是简单的模型还是复杂的模型,恐怕都未必反映实际情况。所以,关键还是在于神经科学的发展,让我们能够彻底清楚神经元的机制。
参考资料: 机器学习 胡浩基 浙江大学