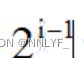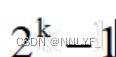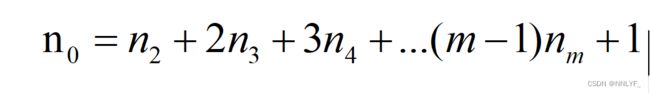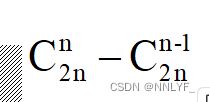数据结构-树与二叉树
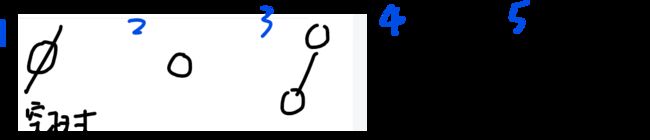
树最适合用来表述（元素之间具有分支层次关系）的数据。
一、二叉树的性质
二叉树的五种基本形态
判断：
1.二叉树第i（i≥1）层上至多有
个结点
2.深度为k（k≥1）的二叉树至多有
个结点。
3.一棵有n个结点的树的所有结点度数之和（边）为n-1.
4.任意二叉树中，若叶子结点（度为0）的个数为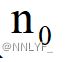
，度为1的结点个数为
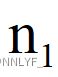，度为2的结点个数为
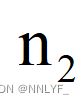，则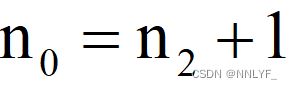
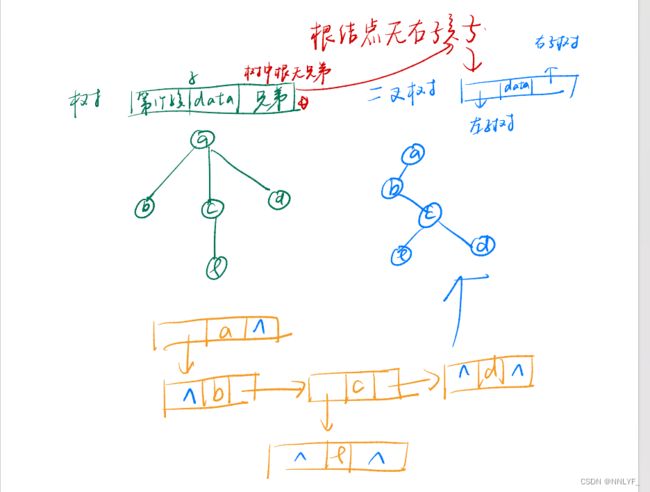
树：
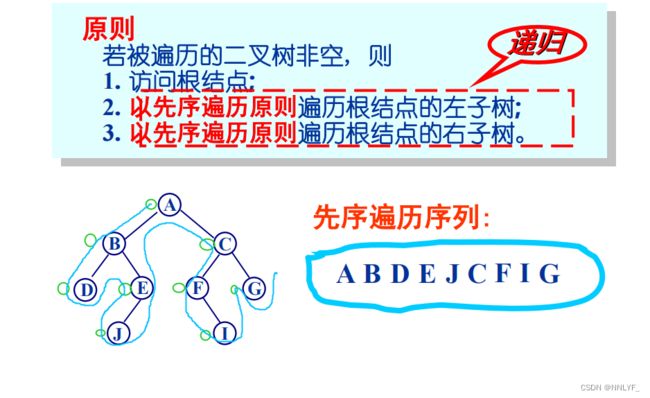
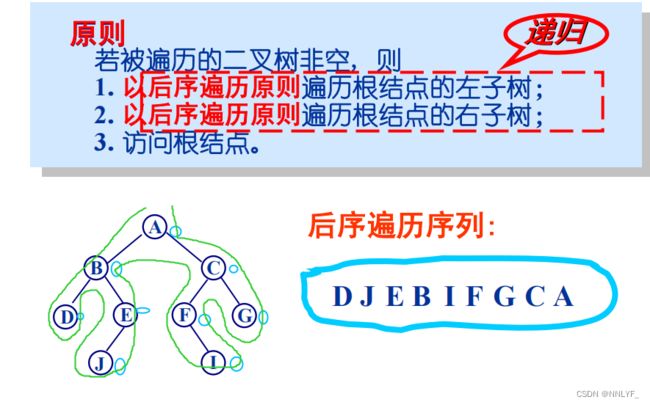
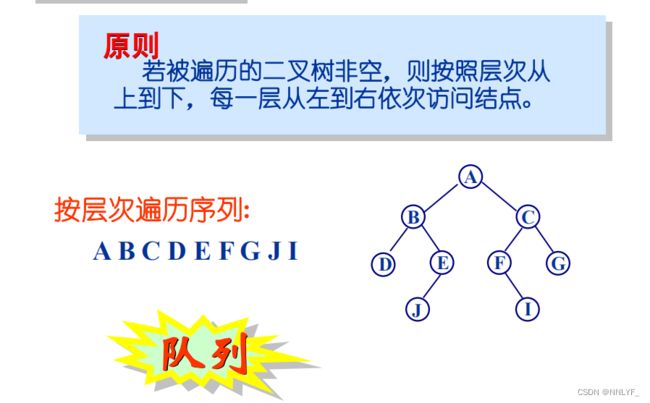
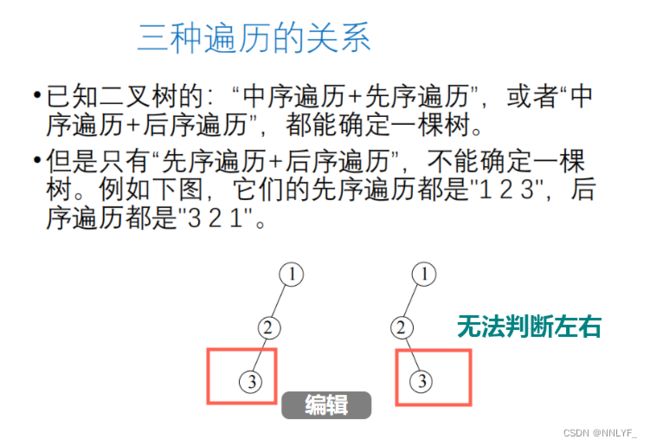
二、二叉树的遍历
快速上手可以看下面这个up主的视频：
【纯干货】三分钟教会你遍历二叉树！学不会举报我！！_哔哩哔哩_bilibili
1.先序遍历
2.中序遍历
3.后序遍历
4.层次遍历（队列实现）
三、二叉树的存储结构
(1) 顺序存储结构
1.完全二叉树的顺序存储结构
2.一般二叉树的顺序存储结构
(2) 链式存储结构
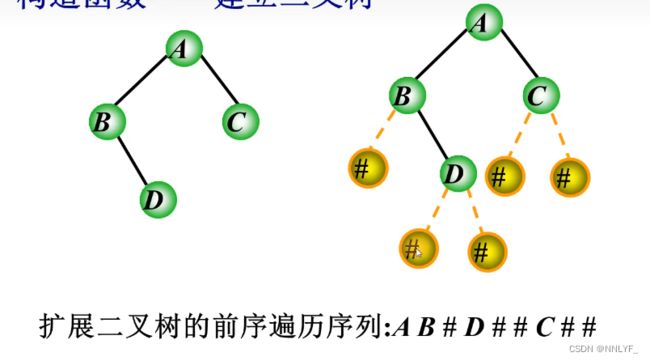
**二叉树的创建（二叉链表*
BTree createTree()
{
BTree T = NULL;//创建空树
char ch;
while (1) {
scanf("%c", &ch); //输入数据
if (ch != '\n' && ch != ' ')
break;
}
if (ch != '#') {
//创建二叉树的根结点，分配内存并初始化指针
T = (BTree)malloc(sizeof(BNode));
T->lchild = T->rchild = NULL;//初始化左子树和右子树
T->data = ch; //读入结点的数据
//递归创建左子树和右子树
T->lchild = createTree();
T->rchild = createTree();
}
return T;
}
**二叉树的创建和四种遍历完整代码**
关于为什么要定义BNode：
#include
#include //内存分配malloc,free
//二叉树的实现-二叉链表（左孩子，右孩子）
typedef struct node {
char data; //结点数据-字符类型
struct node* lchild, * rchild; //左右孩子指针
}BNode, * BTree;
//0.创建二叉树-根据用户的输入
BTree createTree();
//访问二叉树T，打印根结点的数据
void visit(BTree T);
//1.先序遍历DLR，树根-左子树-右子树
void preOrder(BTree T);
//2.中序遍历LDR，左子树-树根-右子树
void inOrder(BTree T);
//3.后序遍历LRD，左子树-右子树-树根
void postOrder(BTree T);
//4.层次遍历-BFS(Breadth First Search)-用队列实现
void layOrder(BTree T);
//循环队列-代码
#define M (1000 + 5)
typedef BTree ElemType;
typedef struct {
ElemType data[M]; //队列的数据
int front, rear; //队列头部和尾部
}SqCyQueue;
//0.初始化队列
void init(SqCyQueue* q);
//1.队列是否为空，如果为空返回1，否则返回0
int isEmpty(SqCyQueue q);
//2.队列是否已满，如果满了返回1，否则返回0
int isFull(SqCyQueue q);
//3.入队，如果成功返回1，否则返回0
int push(SqCyQueue* q, ElemType item);
//4.出队，如果成功返回1，否则返回0
int pop(SqCyQueue* q, ElemType* item);
int main()
{
//1.创建二叉树
BTree T = createTree();
//2.遍历并输出
printf("\n先序遍历：");
preOrder(T);
printf("\n中序遍历：");
inOrder(T);
printf("\n后序遍历：");
postOrder(T);
printf("\n层次遍历：");
layOrder(T);
return 0;
}
//0.创建二叉树-根据用户的输入
BTree createTree()
{
BTree T = NULL;//创建空树
char ch;
while (1) {
scanf("%c", &ch); //输入数据
if (ch != '\n' && ch != ' ')
break;
}
if (ch != '#') {
//创建二叉树的根结点，分配内存并初始化指针
T = (BTree)malloc(sizeof(BNode));
T->lchild = T->rchild = NULL;//初始化左子树和右子树
T->data = ch; //读入结点的数据
//递归创建左子树和右子树
T->lchild = createTree();
T->rchild = createTree();
}
return T;
}
//访问二叉树T，打印根结点的数据
void visit(BTree T)
{
printf("%c", T->data);
}
//1.先序遍历DLR，树根-左子树-右子树
void preOrder(BTree T)
{
if (T == NULL) //空树直接返回
return;
visit(T); //访问树根
preOrder(T->lchild);//先序遍历左子树
preOrder(T->rchild);//先序遍历右子树
}
//2.中序遍历LDR，左子树-树根-右子树
void inOrder(BTree T)
{
if (T == NULL)
return;//空树直接返回
inOrder(T->lchild);//左子树
visit(T);//树根
inOrder(T->rchild);//右子树
}
//3.后序遍历LRD，左子树-右子树-树根
void postOrder(BTree T)
{
if (T == NULL)
return;//空树直接返回
postOrder(T->lchild);//左子树
postOrder(T->rchild);//右子树
visit(T);//树根
}
//4.层次遍历-BFS(Breadth First Search)-用队列实现
void layOrder(BTree T)
{
//1.创建队列并初始化
SqCyQueue q;
init(&q);
//2.树根入队
push(&q, T);
//3.只要队列非空，进入队列循环
while (!isEmpty(q)) {
pop(&q, &T); //出队
visit(T); //打印输出
if (T->lchild != NULL)
push(&q, T->lchild);
if (T->rchild != NULL)
push(&q, T->rchild);
}
}
//0.初始化队列
void init(SqCyQueue* q)
{
q->front = q->rear = 0;
}
//1.队是否为空，如果为空返回1，否则返回0
int isEmpty(SqCyQueue q)
{
return q.front == q.rear;
}
//2.队列是否已满，如果满了返回1，否则返回0
int isFull(SqCyQueue q)
{
return (q.rear + 1) % M == q.front;
}
//3.入队，如果成功返回1，否则返回0
int push(SqCyQueue* q, ElemType item)
{
if (isFull(*q)) {
printf("队列已满，入队失败！\n");
return 0;
}
q->data[q->rear] = item;
q->rear = (q->rear + 1) % M;
return 1;
}
//4.出队，如果成功返回1，否则返回0
int pop(SqCyQueue* q, ElemType* item)
{
if (isEmpty(*q)) {
printf("队列为空，出队失败！\n");
return 0;
}
*item = q->data[q->front];
q->front = (q->front + 1) % M;
return 1;
}
测试样例：
四、二叉树与树、树林之间的转换
1.树与二叉树的转换
给定一棵树，可以找到唯一的一棵二叉树与之对应。
另一种方法：
2.树林与二叉树的转换
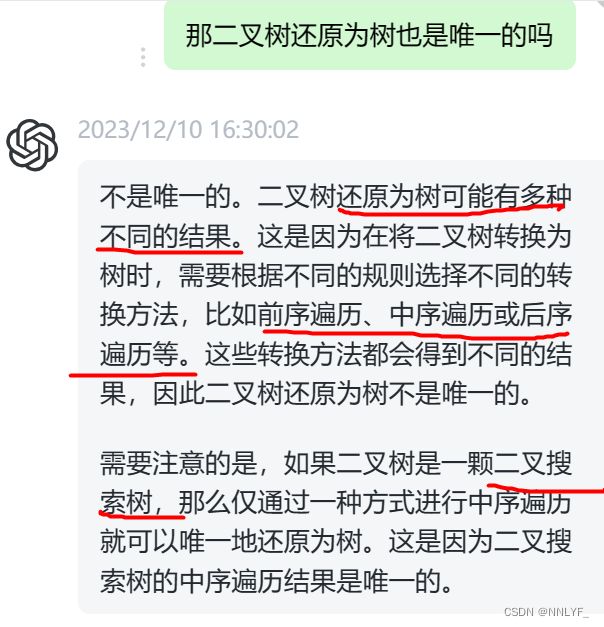
3.二叉树还原为树
不是唯一的
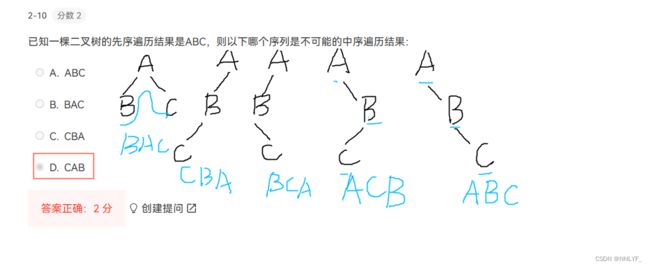
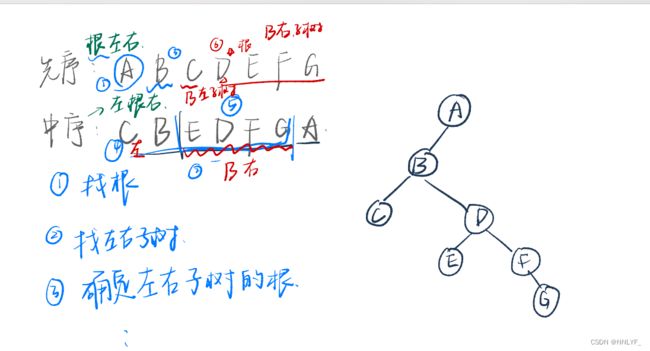
五、由遍历序列恢复二叉树
方法：
1.已知先序和中序：
注意：
代码实现：
//1.根据先序遍历和中序遍历还原二叉树
//先序确定树根，中序分左右
//pre-先序遍历字符串，in-中序遍历字符串，len-长度
BTree createTreePreIn(char* pre, char* in, int len)
{
//1.边界条件，字符串长度为0，则为空树
if (len == 0) return NULL;
//创建一棵二叉树，分配内存
BTree T = (BTree)malloc(sizeof(BNode));
//(BTree) 将malloc函数返回的void*类型指针强制转化为BTree类型指针(类似int *)
// sizeof(BNode)计算BNode类型所占字节数(类似 int）
//2.先序确定树根
T->data = pre[0];
//3.中序分左右
//先找到根在中序序列中的位置
int n = -1;
for (int i = 0; i < len; i++) {
if (in[i] == pre[0])
n = i;
}
//3.1创建左子树,递归调用
T->lchild = createTreePreIn(pre + 1, in, n);
//pre+1 :前序遍历序列中当前节点的下一个节点作为新子树的根节点
// *** in :中序遍历序列作为左子树的中序遍历结果 长度为n 所以只涉及到根左边的部分！！！
//n:左子树的节点个数
//3.2创建右子树
T->rchild = createTreePreIn(pre + n + 1, in + n + 1, len - 1 - n);
return T;
}测试样例: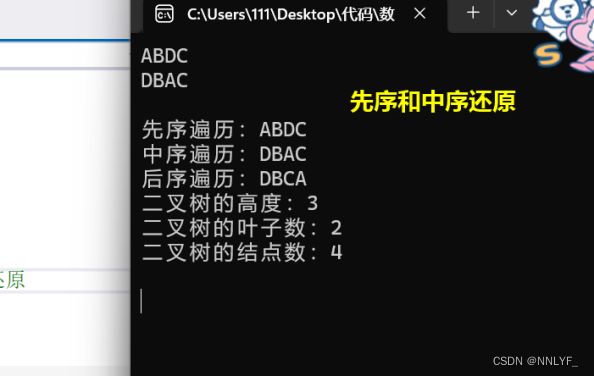
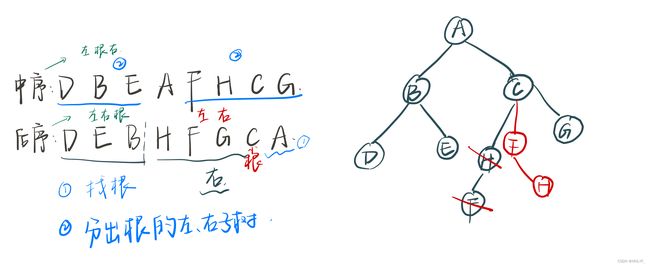
2.已知中序和后序：
代码实现：
//2.根据后序遍历和中序遍历还原二叉树
//后序确定根 中序分左右
BTree createTreePostIn(char* pos,char* in,int len)
{
if (len == 0) return NULL;//长度为0 的空树 返回空指针
BTree T = (BTree)malloc(sizeof(BNode));
//后续遍历确定树根
T->data = pos[len - 1];
//找根在中序序列的位置
int n = -1;
for (int i = 0; i < len; i++)
{
if(in[i]==pos[len-1])
n = i;
}
//递归调用
//右子树 要保证根的全部右子树都在内
//注意顺序 先左子树再右子树
T->lchild = createTreePostIn(pos, in, n);
T->rchild = createTreePostIn( pos + n, in + n + 1, len - n - 1);
return T;
}
测试样例：
六、二叉树的应用
1.求二叉树的高度（深度）
树中结点的最大层数。
代码：
int getHeight(BTree T)
{
if (T == NULL) return 0; //空树高度为0
int lt = getHeight(T->lchild); //左子树高度
int rt = getHeight(T->rchild); //右子树高度
int n = lt;
if (rt > n)
n = rt;
return n + 1; //返回左子树和右子树高度最大值+1
}
2.求二叉树的叶子（子树为0）数
//4.求二叉树的叶子数
//既没有左子树也没有右子树
int getLeafCnt(BTree T)
{
if (T = NULL) return 0;
if (T->lchild == NULL && T->rchild == NULL)
return 1;// 当前节点是叶子节点
// 递归统计左右子树的叶子节点个数
int sum = getLeafCnt(T->lchild) + getLeafCnt(T->rchild);
return sum;
}
3.求二叉树的结点数
//5.求二叉树的结点数
int getNodeCnt(BTree T)
{
if (T == NULL) return 0;
int leftsum = getNodeCnt(T->lchild);//左子树结点数
int rightsum = getNodeCnt(T->rchild);//右子树结点数
return leftsum + rightsum+1;
}
**由N个结点可以构成
种不同形态的二叉树。
4.统计二叉树树中度为1的结点数
int NodeCount( BiTree T){
if(T==NULL) return 0;
if(T->lchild==NULL&&T->rchild!=NULL||T->rchild==NULL&&T->lchild!=NULL){
return 1+NodeCount(T->lchild)+NodeCount(T->rchild);//1 是当前结点自身
}
return NodeCount(T->lchild)+NodeCount(T->rchild);
} **遍历恢复二叉树和应用完整代码**
注意先序中序和中序后序两种情况代码部分注释的情况
#include //输入输出-scanf printf
#include //分配内存-malloc free
#include //字符串函数strlen
const int N = 100 + 5;
//定义二叉树的结点-二叉链表 BinaryTree
typedef struct node {
char data; //结点数据-字符类型
struct node* lchild, * rchild; //左孩子和右孩子
}BNode, * BTree;
//BNode 等价于struct node *BTree等价于struct node*
//11.22二叉树的创建和遍历
//1.先序遍历DLR，树根->左子树->右子树
void preOrder(BTree T);
//2.中序遍历LDR，左子树->树根->右子树
void inOrder(BTree T);
//3.后序遍历LRD，左子树->右子树->树根
void postOrder(BTree T);
//1129二叉树的还原和应用
//1.根据先序遍历和中序遍历还原二叉树
BTree createTreePreIn(char* pre, char* in, int len);
//2.根据后序遍历和中序遍历还原二叉树
BTree createTreePostIn(char* pos, char* in, int len);
//3.求二叉树的高度
int getHeight(BTree T);
//4.求二叉树的叶子数
int getLeafCnt(BTree T);
//5.求二叉树的结点数
int getNodeCnt(BTree T);
int main()
{
char pos[N], in[N];
//,;pre[N],
while (~scanf("%s%s", pos, in)) {
// int n = strlen(pre); //求字符串的长度
int n = strlen(pos); // 求字符串的长度
// BTree T = createTreePreIn(pre, in, n);//先序和中序还原
BTree T = createTreePostIn(pos, in, n);//中序和后序还原
printf("\n先序遍历：");
preOrder(T);
printf("\n中序遍历：");
inOrder(T);
printf("\n后序遍历：");
postOrder(T);
printf("\n二叉树的高度：%d", getHeight(T));
printf("\n二叉树的叶子数：%d", getLeafCnt(T));
printf("\n二叉树的结点数：%d", getNodeCnt(T));
printf("\n\n");
}
return 0;
}
1.根据先序遍历和中序遍历还原二叉树
先序确定树根，中序分左右
pre-先序遍历字符串，in-中序遍历字符串，len-长度
//BTree createTreePreIn(char* pre, char* in, int len)
//{
// //1.边界条件，字符串长度为0，则为空树
// if (len == 0) return NULL; // 返回空指针
// //创建一棵二叉树，分配内存
// BTree T = (BTree)malloc(sizeof(BNode));
// //(BTree) 将malloc函数返回的void*类型指针强制转化为BTree类型指针(类似int *)
// // sizeof(BNode)计算BNode类型所占字节数(类似 int）
//
// //2.先序确定树根
// T->data = pre[0];
// //3.中序分左右
// //先找到根在中序序列中的位置
// int n = -1;
// for (int i = 0; i < len; i++) {
// if (in[i] == pre[0])
// n = i;
// }
// //3.1创建左子树,递归调用
// T->lchild = createTreePreIn(pre + 1, in, n);
// //pre+1 :前序遍历序列中当前节点的下一个节点作为左子树的根节点
// // *** in :中序遍历序列作为左子树的中序遍历结果 长度为n 所以只涉及到根左边的部分！！！
// //n:左子树的节点个数
// //3.2创建右子树
// T->rchild = createTreePreIn(pre + n + 1, in + n + 1, len - 1 - n);
// return T;
//}
//2.根据后序遍历和中序遍历还原二叉树
//后序确定根 中序分左右
BTree createTreePostIn(char* pos,char* in,int len)
{
if (len == 0) return NULL;//长度为0 的空树 返回空指针
BTree T = (BTree)malloc(sizeof(BNode));
//后续遍历确定树根
T->data = pos[len - 1];
//找根在中序序列的位置
int n = -1;
for (int i = 0; i < len; i++)
{
if(in[i]==pos[len-1])
n = i;
}
//递归调用
//右子树 要保证根的全部右子树都在内
//注意顺序 先左子树再右子树
T->lchild = createTreePostIn(pos, in, n);
T->rchild = createTreePostIn( pos + n, in + n + 1, len - n - 1);
return T;
}
//3.求二叉树的高度
int getHeight(BTree T)
{
if (T == NULL) return 0; //空树高度为0
int lt = getHeight(T->lchild); //左子树高度
int rt = getHeight(T->rchild); //右子树高度
int n = lt;
if (rt > n)
n = rt;
return n + 1; //返回左子树和右子树高度最大值+1
}
//4.求二叉树的叶子数
//既没有左子树也没有右子树
int getLeafCnt(BTree T)
{
if (T == NULL) return 0;
if (T->lchild == NULL && T->rchild == NULL)
return 1;// 当前节点是叶子节点
// 递归统计左右子树的叶子节点个数
int sum = getLeafCnt(T->lchild) + getLeafCnt(T->rchild);
return sum;
}
//5.求二叉树的结点数
int getNodeCnt(BTree T)
{
if (T == NULL) return 0;
int leftsum = getNodeCnt(T->lchild);//左子树结点数
int rightsum = getNodeCnt(T->rchild);//右子树结点数
return leftsum + rightsum+1;
}
//访问树根
void visit(BTree T)
{
printf("%c", T->data);
}
//1.先序遍历DLR，树根->左子树->右子树
void preOrder(BTree T)
{
if (T == NULL) return;
visit(T);
preOrder(T->lchild);
preOrder(T->rchild);
}
//2.中序遍历LDR，左子树->树根->右子树
void inOrder(BTree T)
{
if (T == NULL) return;
inOrder(T->lchild);
visit(T);
inOrder(T->rchild);
}
//3.后序遍历LRD，左子树->右子树->树根
void postOrder(BTree T)
{
if (T == NULL) return;
postOrder(T->lchild);
postOrder(T->rchild);
visit(T);
}
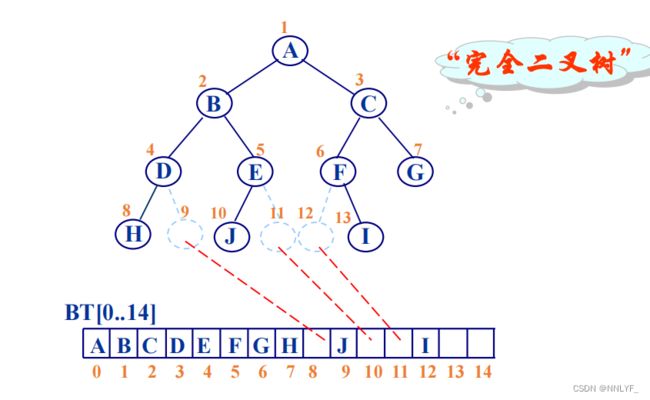
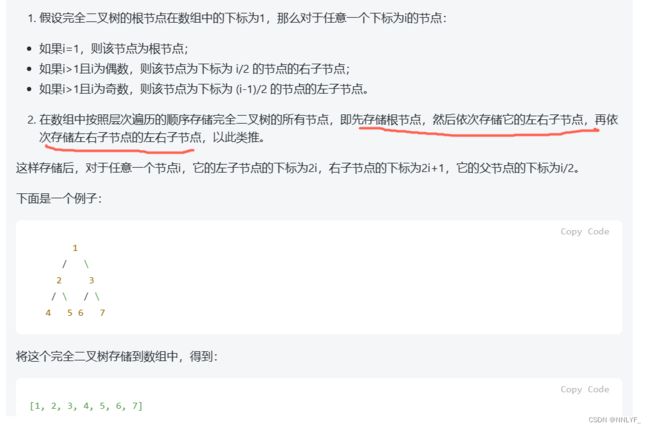
补：完全二叉树
完全二叉树：一棵深度为k的有n个结点的二叉树，对树中的结点按从上至下、从左到右的顺序进行编号，如果编号为i（1≤i≤n）的结点与满二叉树中编号为i的结点在二叉树中的位置相同，则这棵二叉树称为完全二叉树。
可以用数组来储存完全二叉树
**判断一棵树是不是完全二叉树
使用队列来实现：
完整代码：
#define _CRT_SECURE_NO_WARNINGS 1
#include
#include
typedef struct BNode {
char data;
struct BNode* lchild;
struct BNode* rchild;
} BNode, * BTree;
typedef struct SqCyQueue {
BTree* data; // 存储队列元素的数组
int front; // 队头指针
int rear; // 队尾指针
} SqCyQueue;
// 初始化队列
void init(SqCyQueue* q)
{
q->data = (BTree*)malloc(100 * sizeof(BTree));
q->front = q->rear = 0;
}
// 判断队列是否为空
int isEmpty(SqCyQueue q)
{
return q.front == q.rear;
}
// 入队
void push(SqCyQueue* q, BTree x)
{
q->data[q->rear++] = x;
}
// 出队
void pop(SqCyQueue* q, BTree* x)
{
*x = q->data[q->front++];
}
// 创建二叉树
BTree createTree()
{
BTree T = NULL;
char ch;
while (1) {
scanf("%c", &ch);
if (ch != '\n' && ch != ' ')
break;
}
if (ch != '#') {
T = (BTree)malloc(sizeof(BNode));
T->lchild = T->rchild = NULL;
T->data = ch;
T->lchild = createTree();
T->rchild = createTree();
}
return T;
}
//判断是否为完全二叉树
int isCompleteBinaryTree(BTree root)
{
if (root == NULL)
return 1; // 只有一个结点(根)的树也是完全二叉树
SqCyQueue queue;
init(&queue);
int yesEmpty = 0;
push(&queue, root); // 将根结点入队
while (!isEmpty(queue) ){//(queue)作为函数的参数不能省略！！1
BTree Node;
pop(&queue, &Node);//结点出队
if (Node == NULL)
{
yesEmpty = 1;
}
else {
if (yesEmpty) {
return 0;
}
push(&queue, Node->lchild);//左孩子入队
push(&queue, Node->rchild);//右孩子入队
}
}
return 1;
}
int main()
{
printf("请输入二叉树的先序遍历序列（节点之间用空格隔开，空节点用#表示）：\n");
BTree tree = createTree();
int result = isCompleteBinaryTree(tree);
if (result)
printf("该二叉树是完全二叉树。\n");
else
printf("该二叉树不是完全二叉树。\n");
return 0;
}
测试样例：
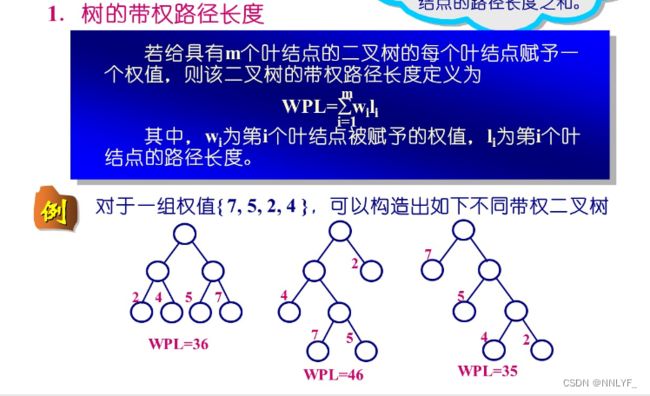
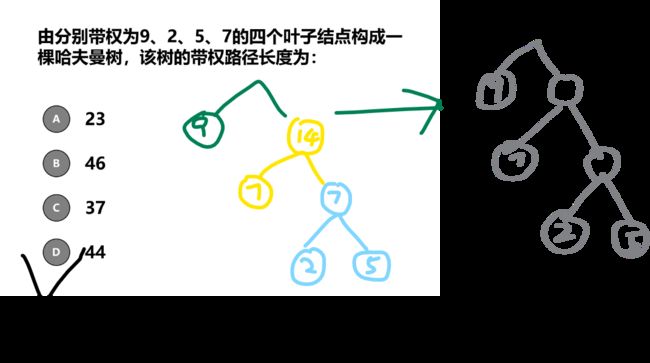
七、哈夫曼树
1.哈夫曼树基本概念
结点之间的路径：这两个结点之间的分治。
路径长度：路径上经过的分支数目。
树的路径长度：根结点到所有的结点的路径长度之和。
不是唯一的： 没有具体算法时，没有指明新生成的二叉树的左、右子树是左大右小还是左小右大；也没有指明两个权值相同时先选择哪个。
2.哈夫曼树的构造
、
3.哈夫曼编码
叶结点数目与需要进行编码的符号数n相等。
前缀编码：任意一个字符的编码不能是另一个（不是下一个）字符编码的前缀。
如：A的编码是00，B的编码是11，G的编码是0011，那么在编码的过程中就无法确定其是字母A和B还是G。
具体方法：
Q：为什么哈夫曼编码可以保证是前缀编码？
哈夫曼树中，每个字符对应于树中的一个叶子节点，而编码则是从根节点到叶子节点的路径上的0和1的序列。字符的编码是通过沿着哈夫曼树从根节点到叶子节点的路径确定的，而不会出现某个字符的编码是另一个字符编码的前缀的情况。
Q：为什么哈夫曼编码可以保证字符编码总长度最短？
哈夫曼编码的构建过程是根据字符频率来建立一个最优的前缀编码树。该树的构建过程中，频率较低的字符被放置在树的较深位置，而频率较高的字符被放置在树的较浅位置。这样，高频字符对应的编码会相对较短，而低频字符对应的编码会相对较长。