数据结构拓扑排序以及关键路径（出度邻接表）C语言 完整代码

一.问题描述

现实生活中一项工程通常会拆分成多个部分来进行，这些部分有些相互之间有发生的前提关系，还有些可以同时发生且不会互相打扰，但是合理且充分的利用时间来完成项目是一个问题。在项目完成的过程中，那些项目的完成时间被压缩可以压缩工程的总时间，以便于提高整个工程的完成效率，而且过程中所有项目不可以产生回环。如何合理的安排项目和找到关键项目是我们所要研究的问题。

二.算法设计

1.关键路径的算法设计

通过问题分析，发现解决问题用图来进行逻辑存储并且使用拓扑排序判断是否有环来寻找关键路径，将项目中的每个事件赋值于图的每个顶点，活动我们定义为图中每个顶点之间的关系并且带有权值以便记忆活动的信息。以此产生一个AOE-网来估算工程的完成时间。

由于整个工程只有一个开始点和一个完成点，故在正常的情况（无环）下，网中只有个入度为零的点叫做（称为源点）和一个出度为零的点（称为汇点）。由于AOV-网中有些活动可以并行的进行，所以完成工程的最短时间是从开始点到完成点的最长路径的长度。路径长度最长的路径叫做关键路径。

我们可以假设开始点事v1，从v1到vi的最长路径长度叫做事件vi的最早发生时间。这个时间决定了所有以vi为尾的弧所表示的活动的最早开始时间。我们用e（i）表示活动ai的最早开始时间。还可以定义一个活动的最迟开始时间l（i），这个是在不推迟整个工程完成的前提下，活动ai最迟必须开始进行的时间。两者之差l（i）—e（i）意味着完成活动ai的时间余量。我们把l（i）==e（i）的活动叫做关键活动。显然，关键路径上的所有活动都是关键活动，因此提前完成非关键活动并不能加快工程的进度。

由上分析可知，辨别关键活动就是要找e(i)=l(i)的活动。为了求得A0E﹣网中活动的 e(i)和l(i)，首先应求得事件的最早发生时间ve(j)和最迟发生时间vl(j)。如果活动Ai，由弧< j , k >表示，其持续时间记为 dut()则有如下关系

e (i)=ve ( j )

l(i)=vl(k)-dut()

求ve (j)和vl(j)需分两步进行:

(1)从 ve (0)=0开始向前递推

ve(j)=Max{ve(i)+dut()}

∈T, j=1,2,...,n-1

其中，T是所有以第 j 个顶点为头的弧的集合。

(2)从 vl (n-1)= ve (n-1)起向后递推

vl(i)=Min{vl(j)-dut()}

∈S, i=n-2,...,0

其中，S 是所有以第 i 个顶点为尾的弧的集合。

这两个递推公式的计算必须分别在拓扑有序和逆拓扑有序的前提下进行。也就是说，ve(j-1)必须在Vj的所有前驱的最早发生时间求得之后才能确定，而 vl( j-1)则必须在Vj的所有后继的最迟发生时间求得之后才能确定。因此,可以在拓扑排序的基础上计算 ve (j-1)和 vl (j-1)。

由此得到如下的所述求关键路径的算法：

（1）输入e条弧，建立AOE-网的存储结构；

（2）从源点v0出发，令ve[0]=0，按拓扑有序求其余各顶点的最早发生时间ve[i]（1

（3）从汇点vn出发，令vl[n-1]=ve[n-1]，按逆序拓扑排序求其余各顶点的最迟发生时间vl（n-2>i>2）；

（4）根据各顶点的ve和vl值，求每条弧s的最早开始时间e（s）和最迟开始时间l（s）。若某条弧满足条件e（s）=l（s），则为关键活动。

2.拓扑排序算法设计

基于上面的AOV-网，我们只需重复下面的两步，直至全部顶点均已输出，或者当前图中不存在无前驱的顶点为止。后一种情况则说明有向图中存在环。

（1）在有向图中选一个没有前驱的顶点并输出之

（2）从图中删除该顶点和所有以它为尾的弧。

三.代码的具体实现

1.首先是邻接表的数据结构类型定义。

typedef struct ArcNode {//表结点的定义
    int adjvex;  //该弧所指向的顶点的位置
    struct ArcNode* nextarc;  //指向下一条弧的指针
    int info;//弧的相关信息
}ArcNode;
typedef struct VNode {  //顶点结点的定义
    VertexType data;  //顶点信息
    ArcNode* firstarc;  //指向第一条依附于该顶点的弧的指针
    int hang;
    int rudushu;
}VNode, AdjList[MAX_VERTEX_NUM];//AdjLst表示邻接表的类型
typedef struct {
    AdjList vertices;    //顶点数组
    int vexnum, arcnum;  //图当前的顶点数和弧数
    int kind;            //图的种类标志
}ALGraph;//图的结构定义

图的存储结构采用邻接表，在邻接表中,对图中每个顶点建立一个单链表,第i个单链表中的结点表示依附于顶点Vi的边(对有向图是以顶点Vi为尾的弧)。每个结点由3个域组成,其中邻接点域(adjvex)指示与顶点Vi邻接的点在图中的位置,链域(nextarc)指示下一条边或弧的结点;数据域(info)存储和边或弧相关的信息，如权值等。每个链表上附设一个表头结点。在表头结点中,除了设有链域(firstarc)指向链表中第一个结点之外,还设有存储顶点Vi的名或其他有关信息的数据域(data)。

图的存储结构使用的是出度领接表，为了方便，在结构体定义的时候用一个rudushu来代表此顶点的如度数，其中的hang其实就是每个顶点的下标。

表结点：

adjvex

nextarc

info

头结点：

data

firstarc

1. 接下来就是主函数，其实就是看个执行顺序就行了。

int main()
{
    ALGraph G;
    Inject(&G);
    TopologicalSort(G);
    CriticalPath(G);
    return 0;
}

先是定义了一个图G，Inject是对图进行初始化，TopologicalSort是拓扑排序，CriticalPath是关键路径。

1. 先看图的初始化。

int LocateVex(ALGraph G, VertexType a)
{
    for (int i = 0; i < G.vexnum; i++)
    {
        if (a == G.vertices[i].data)
        {
            return G.vertices[i].hang;
        }
    }
    return -1;
}

void Inject(ALGraph* G)
{
    //G = (ALGraph)malloc(MAX_VERTEX_NUM * sizeof(ALGraph));
    printf("请输入图的顶点数：");
    scanf_s("%d", &G->vexnum);
    printf("请输入图的边数：");
    scanf_s("%d", &G->arcnum);
    for (int i = 0; i < G->vexnum; i++)
    {
        printf("%d ", i);
        G->vertices[i].hang = i;//将顶点数组每行的信息存进去，方便以后用
        getchar();
        scanf_s("%c", &G->vertices[i].data);//对每个顶点赋值
        //getchar();//清空缓存区*************我的理解就是吃回车
        G->vertices[i].firstarc = NULL;//顶点结点的指针暂时指向空
    }
    VertexType vi, vj;
    int i, j, s;//vi->vj  s是权值的暂时存储
    for (int k = 0; k < G->arcnum; k++)
    {
        printf("按照vi->vj的顺序以及权值：");
        getchar();
        scanf_s("%c", &vi);
        getchar();
        scanf_s("%c", &vj);
        scanf_s("%d", &s);
        i = LocateVex(*G, vi);
        j = LocateVex(*G, vj);//找位置
        ArcNode* p = (ArcNode*)malloc(sizeof(ArcNode));
        p->adjvex = j;//头插法
        p->info = s;
        p->nextarc = G->vertices[i].firstarc;
        G->vertices[i].firstarc = p;
    }
}

以上就是图的初始化，需要先输入图的顶点数以及边数，来大致确定图的结构。

然后使用邻接表的储存结构来存储，第一个for循环来确定顶点表的具体信息来对顶点表初始化。简单来说下一步肯定就是把每个顶点的边的信息用单链表的方式链在顶点表各个顶点的后面。（领接表的结构我写后面了）

第二个循环就是来写入图中每条边的信息，在链接的时候用i和j分别代表指向和被指向，也就是vi->vj的顺序，通过LocateVex来遍历整个顶点表，将j的顶点链接在i的顶点表所在行的后面。（采用头插法）

4.接下来是拓扑排序的具体实现与代码。

int TopologicalSort(ALGraph G)//拓扑排序
{
    int sum = 0;//sum是成功删除掉的顶点数
    int i, k;//
    ArcNode* p;
    for (i = 0; i < G.vexnum; i++)
        G.vertices[i].rudushu = FindInDeree(G, G.vertices[i].hang);//找出入度为0的
    SqStack S;//S1是拓扑排序的逆序存储，S2是正序存储，修火车的方法
    InitStack(&S1);
    InitStack(&S2);
    InitStack(&S);//栈的初始化
    ve = (int*)malloc(G.vexnum * sizeof(int));
    for (int n = 0; n < G.vexnum; n++)
    {
        ve[n] = 0;
    }
    for (int i = 0; i < G.vexnum; i++)//建零入度顶点S
    {
        if (G.vertices[i].rudushu == 0)//入度为0者进栈
            Push(&S, i);//入度为0者进栈
    }
    while (StackEmpty(S))
    {
        i = Pop(&S);
        printf("%c->", G.vertices[i].data);//输出i号顶点并计数
        ++sum;
        Push(&S1, i);
        for (p = G.vertices[i].firstarc; p; p = p->nextarc)
        {
            k = p->adjvex;
            G.vertices[k].rudushu--;//对i号顶点的每个邻接点的入度都减1
            if (!G.vertices[k].rudushu)
                Push(&S, k);
            if ((ve[i] + p->info) > ve[k])//在拓扑排序中就实现ve的修改，取最大值
                ve[k] = ve[i] + p->info;
        }
    }
    if (sum < G.vexnum)
    {
        printf("有回路");
        return 0;
    }
    else
    {
        printf("无回路\n");

        return 1;
    }
}

为了避免重复检测入度为零的顶点，可设置一个栈来暂存所有入度为零的顶点。其中S1和S2是全局变量，S1是拓扑排序的正序存储，S2是拓扑排序的逆序存储。

在栈的使用过程中可以利用栈的先进后出的特性，逆序输出拓扑排序，这样在对于从终点到起点进行分析的最晚开始事件的计算有着异曲同工之妙。

5.关键路径的寻找。

void CriticalPath(ALGraph G)
{
    ArcNode* p;         
    vl = (int*)malloc(G.vexnum * sizeof(int));
    for (int i = 0; i < G.vexnum; i++)//对ltv初始化
        vl[i] = ve[G.vexnum - 1];
    while (StackEmpty(S1))//对vl的修改，取每条边的所得数值的最小值
    {
        int i = Pop(&S1);//利用逆序拓扑排序
        for (p = G.vertices[i].firstarc; p; p = p->nextarc)
        {
            int k = p->adjvex;
            if ((vl[k] - p->info) < vl[i])
                vl[i] = vl[k] - p->info;
        }
    }
    int e, l;
    for (int n = 0; n < G.vexnum; n++)//遍历整个顶点表
    {
        for (p = G.vertices[n].firstarc; p; p = p->nextarc)//遍历每个顶点的链表
        {
            int k = p->adjvex;
            e = ve[n];
            l = vl[k] - p->info;
            if (e == l)
            {
                printf("(%c->%c)", G.vertices[n].data, G.vertices[k].data);
            }
        }
    }
}//关键路径

最晚事件开始时间刚好利用拓扑排序的逆序进行计算。

四.程序测试

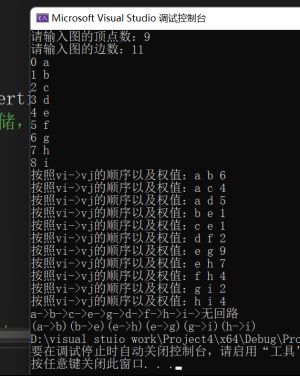
1. 测试用例

1. 测试结果

五.完整代码

#include
#include
#define MAX_VERTEX_NUM 20
#define _NO_CRT_STDIO_INLINE
#define _CRT_INTERNAL_SCANF_SECURECRT
typedef int SElemType;
typedef char  VertexType;//顶点信息数据类型的定义
typedef struct ArcNode {//表结点的定义
    int adjvex;  //该弧所指向的顶点的位置
    struct ArcNode* nextarc;  //指向下一条弧的指针
    int info;//弧的相关信息
}ArcNode;
typedef struct VNode {  //顶点结点的定义
    VertexType data;  //顶点信息
    ArcNode* firstarc;  //指向第一条依附于该顶点的弧的指针
    int hang;
    int rudushu;
}VNode, AdjList[MAX_VERTEX_NUM];//AdjLst表示邻接表的类型
typedef struct {
    AdjList vertices;    //顶点数组
    int vexnum, arcnum;  //图当前的顶点数和弧数
    int kind;            //图的种类标志
}ALGraph;//图的结构定义
typedef struct {
    SElemType* base;  //在栈构造之前和销毁之后，base的值为NULL
    SElemType* top;   //栈顶指针
    int stacksize;    //当前已经分配的存储空间，以元素为单位
}SqStack;
int* ve, * vl;//事件的最早时间和最晚时间    全局变量
SqStack S1;
SqStack S2;


int LocateVex(ALGraph G, VertexType a)
{
    for (int i = 0; i < G.vexnum; i++)
    {
        if (a == G.vertices[i].data)
        {
            return G.vertices[i].hang;
        }
    }
    return -1;
}

void Inject(ALGraph* G)
{
    //G = (ALGraph)malloc(MAX_VERTEX_NUM * sizeof(ALGraph));
    printf("请输入图的顶点数：");
    scanf_s("%d", &G->vexnum);
    printf("请输入图的边数：");
    scanf_s("%d", &G->arcnum);
    for (int i = 0; i < G->vexnum; i++)
    {
        printf("%d ", i);
        G->vertices[i].hang = i;//将顶点数组每行的信息存进去，方便以后用
        getchar();
        scanf_s("%c", &G->vertices[i].data);//对每个顶点赋值
        //getchar();//清空缓存区*************
        G->vertices[i].firstarc = NULL;//顶点结点的指针暂时指向空
    }
    VertexType vi, vj;
    int i, j, s;//vi->vj  s是权值的暂时存储
    for (int k = 0; k < G->arcnum; k++)
    {
        printf("按照vi->vj的顺序以及权值：");
        getchar();
        scanf_s("%c", &vi);
        getchar();
        scanf_s("%c", &vj);
        scanf_s("%d", &s);
        i = LocateVex(*G, vi);
        j = LocateVex(*G, vj);//找位置
        ArcNode* p = (ArcNode*)malloc(sizeof(ArcNode));
        p->adjvex = j;//头插法
        p->info = s;
        p->nextarc = G->vertices[i].firstarc;
        G->vertices[i].firstarc = p;
    }
}

int FindInDeree(ALGraph G, int k)
{
    int sum = 0;    //入度数
    ArcNode* p;   //p指针用来扫描每个顶点所发出的边
    for (int i = 0; i < G.vexnum; i++)//正确循环遍历邻接表每个结点
    {
        p = G.vertices[i].firstarc;
        while (p != NULL)
        {
            if (p->adjvex == k)
            {
                sum++;           //统计顶点的度
                break;
            }
            p = p->nextarc;      //循环遍历结点的所有弧
        }
    }
    return sum;          //返回入度
}

int InitStack(SqStack* S)  //创造一个空栈
{
    S->base = (SElemType*)malloc(MAX_VERTEX_NUM * sizeof(SElemType));
    if (!S->base)exit(1);   //判空
    S->top = S->base;
    S->stacksize = MAX_VERTEX_NUM;
    return 1;
}

void Push(SqStack* S, int k)
{
    *S->top++ = k;
}
int StackEmpty(SqStack S)
{
    if (S.top == S.base)
    {
        return 0;
    }
    return 1;
}

int Pop(SqStack* S)
{
    if (S->top == S->base) return 0;
    int i;
    i = *--S->top;
    return i;
}

int TopologicalSort(ALGraph G)//拓扑排序
{
    int sum = 0;//sum是成功删除掉的顶点数
    int i, k;//
    ArcNode* p;
    for (i = 0; i < G.vexnum; i++)
        G.vertices[i].rudushu = FindInDeree(G, G.vertices[i].hang);//找出入度为0的
    SqStack S;//S1是拓扑排序的逆序存储，S2是正序存储，修火车的方法
    InitStack(&S1);
    InitStack(&S2);
    InitStack(&S);//栈的初始化
    ve = (int*)malloc(G.vexnum * sizeof(int));
    for (int n = 0; n < G.vexnum; n++)
    {
        ve[n] = 0;
    }
    for (int i = 0; i < G.vexnum; i++)//建零入度顶点S
    {
        if (G.vertices[i].rudushu == 0)//入度为0者进栈
            Push(&S, i);//入度为0者进栈
    }
    while (StackEmpty(S))
    {
        i = Pop(&S);
        printf("%c->", G.vertices[i].data);//输出i号顶点并计数
        ++sum;
        Push(&S1, i);
        for (p = G.vertices[i].firstarc; p; p = p->nextarc)
        {
            k = p->adjvex;
            G.vertices[k].rudushu--;//对i号顶点的每个邻接点的入度都减1
            if (!G.vertices[k].rudushu)
                Push(&S, k);
            if ((ve[i] + p->info) > ve[k])//在拓扑排序中就实现ve的修改，取最大值
                ve[k] = ve[i] + p->info;
        }
    }
    if (sum < G.vexnum)
    {
        printf("有回路");
        return 0;
    }
    else
    {
        printf("无回路\n");

        return 1;
    }
}

void CriticalPath(ALGraph G)
{
    ArcNode* p;         
    vl = (int*)malloc(G.vexnum * sizeof(int));
    for (int i = 0; i < G.vexnum; i++)//对ltv初始化
        vl[i] = ve[G.vexnum - 1];
    while (StackEmpty(S1))//对vl的修改，取每条边的所得数值的最小值
    {
        int i = Pop(&S1);//利用逆序拓扑排序
        for (p = G.vertices[i].firstarc; p; p = p->nextarc)
        {
            int k = p->adjvex;
            if ((vl[k] - p->info) < vl[i])
                vl[i] = vl[k] - p->info;
        }
    }
    int e, l;
    for (int n = 0; n < G.vexnum; n++)//遍历整个顶点表
    {
        for (p = G.vertices[n].firstarc; p; p = p->nextarc)//遍历每个顶点的链表
        {
            int k = p->adjvex;
            e = ve[n];
            l = vl[k] - p->info;
            if (e == l)
            {
                printf("(%c->%c)", G.vertices[n].data, G.vertices[k].data);
            }
        }
    }
}//关键路径



int main()
{
    ALGraph G;
    Inject(&G);
    TopologicalSort(G);
    CriticalPath(G);
    return 0;
}