代码随想录day4--链表进阶
LeetCode24.两两交换链表中的节点
题目描述:
给你一个链表,两两交换其中相邻的节点,并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题(即,只能进行节点交换)。
示例 1:
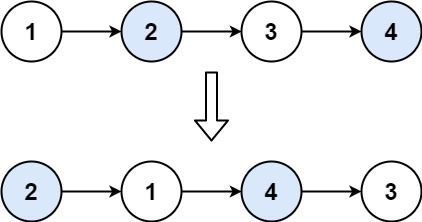
输入:head = [1,2,3,4] 输出:[2,1,4,3]
示例 2:
输入:head = [] 输出:[]
示例 3:
输入:head = [1] 输出:[1]
解题思路:
·看到题目的第一个念头是使用双指针,观看题解发现,题解也是使用的类似的双指针的解法
·本题依旧是使用的虚拟头结点,会方便很多,否则每次针对头结点(没有前一个指针指向头结点),要单独处理,很麻烦
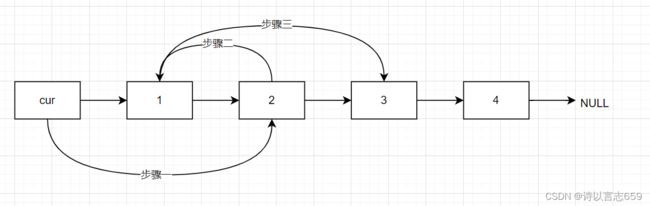
·以示例为例画出下图
进行操作后,链表如下:
根据图解进行题解
代码如下:
class Solution {
public:
ListNode* swapPairs(ListNode* head) {
ListNode* dummyHead = new ListNode(0);//设置一个虚拟头结点
dummyHead->next = head;//将虚拟头结点指向head,这样方便后续做删除操作
ListNode* cur = dummyHead;
while(cur->next != nullptr && cur->next->next != nullptr){//注意&&前后顺序不能调换
ListNode* temp;//临时节点1
ListNode* temp1;//临时节点2
temp = cur->next;
temp1 = cur->next->next->next;
cur->next = cur->next->next;//步骤一
cur->next->next = temp;//步骤二
cur->next->next->next = temp1;//步骤三
cur = cur->next->next;//cur移动两位后,准备下一次交换
}
return dummyHead->next;
}
};·时间复杂度:O(n)
·空间复杂度:O(1)
难点:
这道题的不是单纯单独改变节点内的值,而是需要实际的进行节点交换,一定要用虚拟头节点进行操作,否则会麻烦很多。交换相邻两个元素,一定要画图操作,同时要操作多个指针负责真的很容易乱,而且画图便于操作先后顺序。
总结:链表的操作不是特别困难,但是过程比较繁琐,尤其是变化时需要时刻注意到索引的变化,特别是要前一个索引节点,决定了是否能正确变化。
LeetCode19.删除链表的倒数第N个节点
题目描述:
给你一个链表,删除链表的倒数第 n 个结点,并且返回链表的头结点。
示例 1:
输入:head = [1,2,3,4,5], n = 2 输出:[1,2,3,5]
示例 2:
输入:head = [1], n = 1 输出:[]
示例 3:
输入:head = [1,2], n = 1 输出:[1]
解题思路:
·删除节点的操作我们之前已经掌握,这里不再过多赘述
·最大的问题就是如何做到如何正确找到倒数第N个节点,这里可以巧妙的使用双指针,因为链表中对当前节点进行操作需要知道前一个结点的索引地址,所以就定义一个慢指针,一个快指针,让fast移动n步,然后让fast和slow同时移动,知道fast指向链表末尾,然后再删除slow指向的节点即可。
代码如下:
class Solution {
public:
ListNode* removeNthFromEnd(ListNode* head, int n) {
ListNode* dummyHead = new ListNode(0);
dummyHead->next = head;
ListNode* fast = dummyHead;
ListNode* slow = dummyHead;
while(n-- && fast != nullptr){
fast = fast->next;
}
fast = fast->next;
while(fast != nullptr){
fast = fast->next;
slow = slow->next;
}
ListNode* temp = slow->next;
slow->next = slow->next->next;
delete temp;
return dummyHead->next;
}
};·时间复杂度:O(n)
·空间复杂度:O(1)
总结
这道题在难度上并没有什么太大问题,主要是解法比较难想到,可以说比较新奇。又学到了一个双指针的妙用。
LeetCode142.环形链表II
题目描述:
给定一个链表的头节点 head ,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。如果 pos 是 -1,则在该链表中没有环。注意:pos 不作为参数进行传递,仅仅是为了标识链表的实际情况。
不允许修改 链表。
示例 1:
输入:head = [3,2,0,-4], pos = 1 输出:返回索引为 1 的链表节点 解释:链表中有一个环,其尾部连接到第二个节点。
示例 2:
输入:head = [1,2], pos = 0 输出:返回索引为 0 的链表节点 解释:链表中有一个环,其尾部连接到第一个节点。
示例 3:
输入:head = [1], pos = -1 输出:返回 null 解释:链表中没有环。
解题思路:
·设置两个指针,一个快指针,一个慢指针,当快指针等于慢指针时,说明存在环形链表
·但是找到环的入口是在看了题解之后才会写,题解的想法特别巧妙,当两个指针相遇后,从头结点出发一个指针,从相遇节点也发出一个指针,这两个指针每次只走一个节点,那么当这两个指针相遇的时候就是环形如果的节点
代码如下:
class Solution {
public:
ListNode *detectCycle(ListNode *head) {
ListNode* fast = head;
ListNode* slow = head;
while(fast != nullptr && fast->next != nullptr){
slow = slow->next;
fast = fast->next->next;
if(slow == fast){//表示快慢指针相遇
ListNode* index1 = fast;
ListNode* index2 = head;
while(index1 != index2){
index1 = index1->next;
index2 = index2->next;
}
return index2;
}
}
return nullptr;
}
};·时间复杂度:O(n),快慢指针相遇前,指针走的次数小于链表长度,快慢指针相遇后,两个index指针走的次数也小于链表长度,总体为走的次数小于2n
·空间复杂度:O(1)
总结:这道题依旧在代码上依旧没有什么难度,想法也是特别的独特,所以,写代码要的不少写的过程,而是要锻炼思考的思维过程。今天的题目均是双指针的妙用,不得不感叹双指针的强大,发现我对双指针的了解知之甚少,还要加强对双指针的练习。经过今天的练习,对链表的基础已基本掌握。