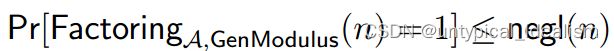密码学理论09：数论和密码学困难问题
整数模N
符号：Z；N；Z>0
gcd（a，N）：对于 a, N ∈ Z ，令 gcd(a, N) 为最大的 d ∈ Z>0 ，使得 d|a 和 d|N。
ZN；ZN*；
（N）；
除法，余数，模数
令a为整数且令N为正整数。那么存在唯一的整数 q、r，其中 a = qN + r 且 0 ≤ r < N。——(q, r) ← div(a, N)
- 称 q 为商，r 为余数
- 那么a mod N = r ∈ ZN
同余：a ≡ b (mod N) 如果 a mod N = b mod N 或等效于 N|(a − b)。
(a + b) mod N = (a mod N + b mod N) mod N
(a · b) mod N = (a mod N · b mod N) mod N
群
一个（有限）群 G 是一个具有二元运算的（有限）非空集 ，其中以下属性成立：
- 闭包：对于所有的 g，h ∈ G，g·h ∈ G
- 恒等式：存在 e ∈ G s.t.对于所有 g ∈ G，我们有 e · g = g = g · e
- 逆元：对于所有 g ∈ G 存在 h ∈ G s.t. g·h=e=h·g
- 结合性：对于所有 g, h, f ∈ G，满足 (g · h) · f = g · (h · f)
如果对于所有 g, h ∈ G 我们有 g · h = h · g，则一个群是可交换的（或阿贝尔群）
模指数
g^m := g · ...g(m 次)，对于 m ∈ N 和 m · g = g + ... + g (m 次)（对于加法群）
对于所有 i, j ∈ Z ：
- g^i+j = g^i · g^j
- g^ij = (g^i )^j = (g^j )^i
- g^−i = (g^i )^−1 = (g^−1 )^i
群的阶
阶：如果 G 是有限的，则 m := |G|称为群的阶
设 G 是一个有限群，m = |G|是群的阶。那么对于任何元素 g ∈ G，g^m = 1。
设 G 是一个有限群，其中 m = |G| > 1. 然后对于任何 g ∈ G 和任何整数 x，我们有 g^x = g^(x mod m)
摸指数运算
——快速求幂：
循环群
让我们考虑一个 m 阶的有限群 G 并写成 < g >= {g0, g1, ...}
设 i ≤ m 为 g^i = 1 的最小正整数，则上述序列在 i 项后重复，(gi = g^0 , gi+1 = g , ...) 和 < g >= {g^0 , g^1 , ..., g^i−1}。
我们称 i 为 g 的阶，< g >⊆ G 称为 g 生成的子群。
如果存在阶数为 m := |G| 的元素 g，则称 G 是循环的。我们写 < g >= G。
定理：令 G 为有限群，且 g ∈ G 为 i 阶元素。那么对于任何整数 x，我们有 g^x = g [x mod i]；令 G 为 m 阶有限群，并称 g ∈ G 具有 i 阶，则i | m。
定理：如果 p 是素数，则 Z ∗ p 是一个 p − 1 阶循环群。
随机质数
设置 t=3n^2 我们在 t 次迭代中没有命中任何素数的概率可以忽略不计。
概率素性检测
尽管有确定性素数测试，但我们使用概率测试（因为它们更有效）。形式化的概率测试：如果输入 n 是素数，算法总是输出“素数”。如果 n 是复合的，那么算法几乎总是输出“复合”，但可能会以一定的概率输出错误的答案（“质数”）（复合是确定的，对于质数它可能会出错）。
大素数分解
每个整数 N > 1 都可以唯一地写为 N = 
，pi 是不同的素数，对于所有 i，ei ≥ 1。
给定分解，很容易计算N，对于某些形式的N，计算因式分解很困难。——如果要分解的数字只有大的素因子，则最难。
求任何给定 N 的因子的简单算法是简单除法。——指数时间复杂度
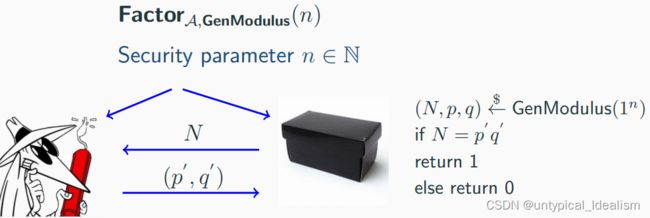
设 GenModulus 是一个多项式时间算法，它在输入 1 n 上输出 N、p、q，其中 N = pq，p、q 是 n 位素数。
大素数分解问题是困难问题，如果对于所有 PPT敌手A 都存在一个可忽略的函数使得：
RSA假设
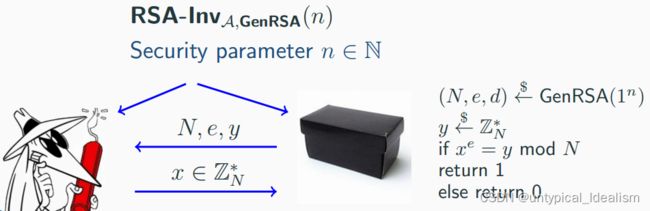
设 GenRSA 是一个多项式时间算法，在输入 1^n 上输出 (N, e, d)，其中 N = pq 和 p, q 是 n 位素数，e, d > 0 是整数 s.t. gcd(e, φ(N)) = 1 和 ed = 1 mod φ(N)。
RAS问题是困难问题，如果对于所有 PPT敌手A 都存在一个可忽略的函数使得：
离散对数问题
我们考虑具有生成元 g 的 q 阶循环群 G，因此 G = {g^0 , ..., g^q−1}。
DL 问题：给定 h = g^x 以找到唯一的 x ∈ Zq。
我们现在来看看两个相关但弱于 DLP 的问题：计算（CDH）和决策 Diffie-Hellman（DDH 问题）——
让 DHg(h1, h2) := g^logg (h1)·logg (h2) 。如果 h1 = g^x1，h2 = g^x2，则 DHg(h1, h2) = g^x1x2 = h1^x2 = h2^x1 。
CDH问题：给定 (G, q, g, h1, h2) 计算 DHg(h1, h2)。
DDH问题：给定 (G, q, g) 和均匀随机 h1, h2 ∈ G，区分 DHg(h1, h2) 和均匀随机 h'∈ G。
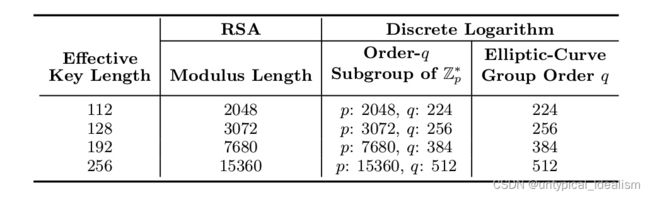
离散对数难解群的选择：
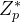（没有素数阶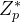）- 的素数阶 q 子群
- 椭圆曲线群
