leetcode - 1457. Pseudo-Palindromic Paths in a Binary Tree

Description

Given a binary tree where node values are digits from 1 to 9. A path in the binary tree is said to be pseudo-palindromic if at least one permutation of the node values in the path is a palindrome.

Return the number of pseudo-palindromic paths going from the root node to leaf nodes.

Example 1:

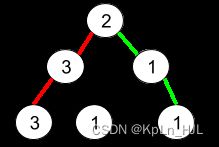
Input: root = [2,3,1,3,1,null,1]
Output: 2 
Explanation: The figure above represents the given binary tree. There are three paths going from the root node to leaf nodes: the red path [2,3,3], the green path [2,1,1], and the path [2,3,1]. Among these paths only red path and green path are pseudo-palindromic paths since the red path [2,3,3] can be rearranged in [3,2,3] (palindrome) and the green path [2,1,1] can be rearranged in [1,2,1] (palindrome).

Example 2:

Input: root = [2,1,1,1,3,null,null,null,null,null,1]
Output: 1 
Explanation: The figure above represents the given binary tree. There are three paths going from the root node to leaf nodes: the green path [2,1,1], the path [2,1,3,1], and the path [2,1]. Among these paths only the green path is pseudo-palindromic since [2,1,1] can be rearranged in [1,2,1] (palindrome).

Example 3:

Input: root = [9]
Output: 1

Constraints:

The number of nodes in the tree is in the range [1, 10^5].
1 <= Node.val <= 9

Solution

The path is pseudo-palindromic if the frequency of each node has at most 1 odd number. So use pre-order traverse to go through all the nodes, and use a map to keep track of each distinct value’s frequency.

Time complexity: $o(n)$
Space complexity: $o(n)$

Code

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def pseudoPalindromicPaths (self, root: Optional[TreeNode]) -> int:
        val_cnt = {}
        stack = [(root, 0)]
        res = 0
        while stack:
            node, status = stack.pop()
            if status == 0:
                val_cnt[node.val] = val_cnt.get(node.val, 0) + 1
                stack.append((node, 1))
                if node.right:
                    stack.append((node.right, 0))
                if node.left:
                    stack.append((node.left, 0))
                # if node is a leaf
                if not node.left and not node.right:
                    # pseudo-palindromic only when at most 1 odd frequency
                    odd_cnt = 0
                    for fre_cnt in val_cnt.values():
                        if fre_cnt % 2 == 1:
                            odd_cnt += 1
                    res += (1 if odd_cnt <= 1 else 0)
            else:
                val_cnt[node.val] -= 1
        return res