学习笔记-李沐动手学深度学习（三）（10-11，隐藏层、多层感知机、激活函数、模型超参数选择、欠过拟合）

总结

多体会（宏观、哲学）

【深度学习的核心】首先是要模型足够大，在此基础上通过各种手段 来控制模型容量，使得最终得到较小的泛化误差
【一般深度学习特指神经网络 这一块】

【学习的核心是要学习 本质上不变的那些核心思想，如欠过拟合、数据集怎么弄、训练误差泛化误差等等，因为很可能过几年有新的语言、新的技术出现。整个工科本质上都差不多，从某个方向深入学习到精髓，很容易向其他工科迁移】

世界上有三种东西：
艺术：我做了一件事，但我也不知道怎么解释，我觉得这样好看点
工程：我做的事情可以通过实际来验证，都可以通过定理来描述
科学：去理解为什么
深度学习（神经网络）一开始是艺术（我有个想法 且 也能work，得想个理由如何解释，虽然 暂时也不知道如何解释是最合理的），但只要你能work，总有人帮你找到理由去解释为何work（此即engineer的任务）
比如蒸汽机先出现，解释蒸汽机的原理的物理学知识是100年后才出来的，有一定的滞后性

【多层感知机】经验：网络是宽点好（即 隐藏层数少，每个隐藏层比较宽）还是深点好（有多个隐藏层）
一般来说 多隐藏层时， 前面到后面 隐藏层宽度越来越小
（即
（1）从第一个隐藏层逐步压缩input并提炼信息，而不是一次压的特别小
或
（2）在第一个隐藏层开始 先将input放大，然后再逐步压缩（即减小隐藏层宽度），如下图 ）

但一般不会 一开始就先把图片压缩到很小再放大，因为这样会 丢失很多特征信息（但是后面CNN也有这么做的，到时再看吧）

模型参数与超参数的区别

模型参数指w权重、b偏差的值
超参数：如人为选择模型（是线性模型还是多层感知机 还是其他模型），如果是多层感知机 选多少层、每层多大， 训练的lr多少
个人概括：超参数就是人为可设置、人为可选的参数；模型参数就是 通过训练 模型自己得到的参数
hyperparameter

多层感知机与SVM

学术界就是个时尚界，每过几年就有不同的流行的东西
【SVM不怎么需要调参，而且数学理论有人推崇】

4.从时间顺序上来说：多层感知机是在SVM之前出现的
多层感知机虽然解决了XOR问题，但是 其弊端是需要 选择超参数；
但是SVM对于超参数不敏感， 最中间结果好坏受超参数影响很小。SVM的优化更容易实现（无需 SGD这种东西）。SVM有很漂亮的数学定理，有很多数学性的东西，如果 二者作用效果差不多 当然使用SVM。

现在之所以推荐用多层感知机MLP是因为，当问题变了后 你想改成别的神经网络，MLP的代码只需要简单修改、大体的优化算法等内容基本无修改 即可实现，而用SVM的改动量较大

关于神经网络层数的说明

【隐藏层一般都是带非线性激活函数的】不带隐藏层的网络就是线性网络模型wx+b
【神经网络层数的说明】通常来讲，一层是指带权重的
一般来说，一层是包括【w、输入、b等权重的计算】+【（非线性）激活函数sigma】的。
如吴恩达，一般将input不算层数， 是所有的隐藏层+output 层 = 层数（当然也能理解为 input+所有隐藏层 不算输出层，其实意思是一样的，只是一般 不算input层，算output层）

个人感觉看几层没有绝对的定论，只是比表述、描述方式不同
感觉也不一定,吴恩达说过几层有的是不包括输入层的,也就是看权重有几层.但在其他一些地方就包括了输入层,这个几层无伤大雅
【下图无论用哪种看法 看 都是两层】每个箭头相当于可以学习的权重

吴恩达中：

关于W、X、b的维度说明

【总结】写W·X或X·W 或有时W^T都没关系，意义都是 权重W和输入X做矩阵运算，各种写法的目的最终都是为了 能使二者的运算满足矩阵乘法运算规则。
怎么写都没有本质区别，和你如何定义 矩阵、向量有关（比如矩阵是mxn还是nxm，向量是行还是列）

如下图w写4x5的shape或5x4均可， 具体写法要看 输入X是怎么定义的

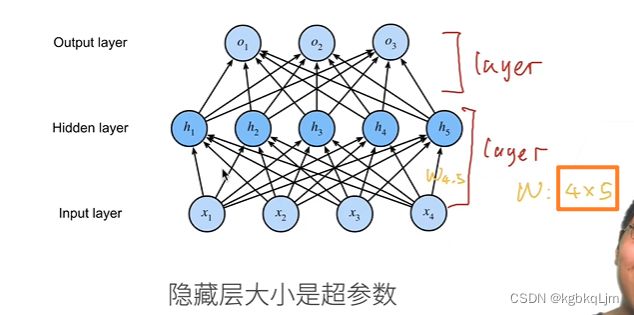
注意：是否需要转置和你的声明有关，最终只要是能满足X和W能做矩阵乘法运算，如：X·W或W^T`X即可
H = relu(X @ W1 + b1) 如此处参与计算的X的shape为（自动计算，num_inputs）、W.shape为（num_inputs, num_hiddens）那么 直接X·W就满足矩阵乘法了，就无需对W转置了

本课程中隐藏层大小

即单个隐藏层如何设计，即有多少个神经元，即 待学习的权重如何

10-多层感知机+代码实现

感知机（二分类问题）

个人理解：
感知机即单层神经网络
多层感知机：多层神经网络

【多层感知器（多层感知机、multilayer perceptron）】就是如下图这种基本的多层的神经网络的宏观称呼

基本概述

六七十年前的模型：
加粗为向量，<>内积

从图像上来看感知机： 有多个输入，一个输出（即二分类问题）
① 线性回归输出的是一个实数，感知机输出的是一个离散的类。

训练感知机

初始化w、b均为0

① 如果感知机预测分类正确的话，yi*[+b]为正数，负号后变为一个负数，max后输出为0，则梯度不进行更新。
② 如果分类错了，yi*[+b]为负数，则 下图中的if判断就成立了，就梯度进行更新，对参数w、b进行一次更新。
重复上述过程，直到所有类都分类正确

等价于每次拿一个样本去基于梯度下降进行更新（原始的感知机并未使用随机方法）
即下图中的感知机过程 等价于下图中下面红框的损失函数
yi应该是第i个样本的真实类别，绿框是 预测类别结果

例子：狗、猫分类
domestication：驯化；驯养
当前分类模型的权重对应 黑色线

当再来一个狗时，原权重不对， 向下更新一点到 下图黑色线
下面的几个图是重复这个过程，直到对所有样本都分类正确

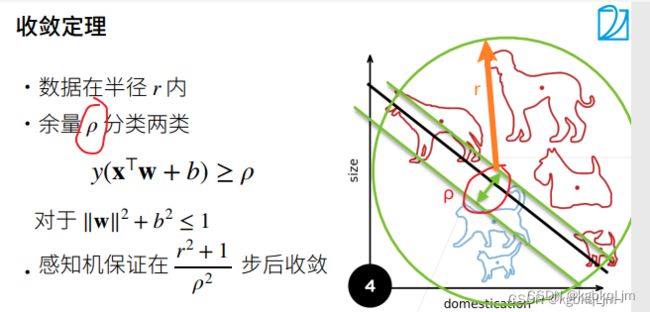
收敛定理：什么时候才能够停止
r越大，数据越大，收敛越慢
ρ越小，你的 预测模型的波动范围就不能太大，留给你的余量就小，那么花的时间自然就长

XOR：异或
感知机无法拟合XOR函数：红色代表一类（如-1），绿色代表一类（如+1），感知机（线性模型）无法产生线性分割面 将 共同的类别分割在一边（如下图中无法用一条直线将 相同颜色的点分割在一边）


但是可以通过多层感知机解决上述问题

多层感知机（MLP、multilayer perceptron）

下图中各个隐藏层大小即指 每个隐藏层样子如何设计（即有多少个节点及节点的权重）

个人理解多层感知机：一定是个非线性模型。线性模型中 加入一或多个非线性隐藏层（即含非线性激活函数）后的 模型
【作用】其解决了 感知机（线性模型）不能拟合XOR的局限性（通过加入隐藏层和激活函数，感觉 图片中是 将 隐藏层节点和激活函数画在一起了，有些图片也会把二者分开画）

【引言】基于单线性模型解决不了XOR问题
根据上节，单线性模型肯定不能解决XOR问题，那么分步来看（即如果一步做不了，就改成多步，分别学出两个不同的简单函数，最后将 二者组合起来）：
蓝色线y 根据 x的正负来分隔（分开了1、3 和 2、4）；
黄色线x 根据y的正负来分隔（分开了1、2和3、4）；
然后对结果做同或运算，得到product

下图中横纵轴分别为 两个特征，颜色是其label

多层感知机解决单分类问题

【正文】

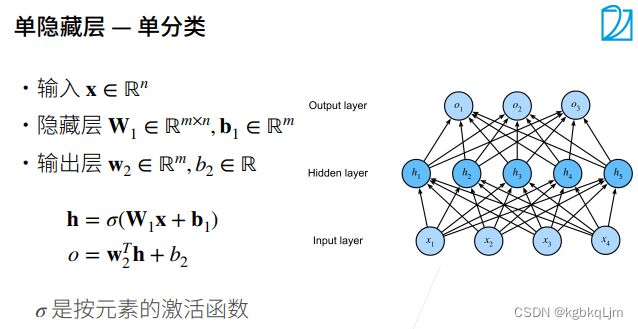
我们能做的就是设置隐藏层大小，因为输入输出层的大小 已经固定了（实际需求）

具体看下：
输入为一个n维向量
W1：mxn矩阵，b1：长为m的向量
h：每个隐藏层的输出
提示：下面 左边参数和右边图无关

hence：因此

如果用线性的激活函数sigma，则 最后的模型还是线性模型

激活函数（sigmoid、Tanh、ReLU）

sigmoid

Tanh

【常用】ReLU

【tips】选择激活函数的类型远远没有 选择隐藏层大小（即如隐藏层超参数的学习）重要，因此一般用ReLU即可

【简单、快捷】指数运算的开销（时间、性能空间等）很大，ReLU相较于前面的激活函数，无指数运算

多层感知机解决多类分类问题（应用了softmax）

多类分类与softmax的唯一区别就是多加了 隐藏层，其他没有本质区别
如下图中 没有中间的隐藏层，就是简单的softmax回归；
如下图，则为 多层感知机

多层感知机解决多分类问题时，除了 向量、标量、矩阵等维度方面的变化，还有 多了一步softmax

多隐藏层的多层感知机

h为每个隐藏层的输出
最后一层无需激活函数（即 下图中 sigma）

【与之前单分类问题多层感知机的区别】超参数变多了（即 选多少个隐藏层，以及每个隐藏层是什么样的（有经验在里面的））
经验：网络是宽点好（即 隐藏层数少，每个隐藏层比较宽）还是深点好（有多个隐藏层）
一般来说 多隐藏层时， 前面到后面 隐藏层宽度越来越小
（即
（1）从第一个隐藏层逐步压缩input并提炼信息，而不是一次压的特别小
或
（2）在第一个隐藏层开始 先将input放大，然后再逐步压缩（即减小隐藏层宽度），如下图 ）

【W是否转置的说明】注意：是否W需要转置和你的声明有关，最终只要是能满足X和W能做矩阵乘法运算，如：X·W或W^T`X即可

但一般不会 一开始就先把图片压缩到很小再放大，因为这样会 丢失很多特征信息（但是后面CNN也有这么做的，到时再看吧）

【具体可看视频 P2多层感知机 17:00】https://www.bilibili.com/video/BV1hh411U7gn/?p=2&spm_id_from=pageDriver&vd_source=e81e116c4ffe5e79d4bc44738263eda4

代码实现

从零实现

注意：是否需要转置和你的声明有关，最终只要是能满足X和W能做矩阵乘法运算，如：X·W或W^T`X即可
H = relu(X @ W1 + b1) 如此处参与计算的X的shape为（自动计算，num_inputs）、W.shape为（num_inputs, num_hiddens）那么 直接X·W就满足矩阵乘法了，就无需对W转置了

import torch
from torch import nn
from d2l import torch as d2l
# 0.
batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

# 1.实现一个具有单隐藏层的多层感知机，它包含256个隐藏单元
num_inputs, num_outputs, num_hiddens = 784, 10, 256 # 输入784、输出10是数据决定的，256是调参自己决定的（超参数，选的是10-784之间的一个数）
# 初始化w1的行数为784、列数256。此处加不加nn.Parameter都行。
# 为什么此处要随机初始化randn，而不是全初始化为0？（弹幕说：设置为零的话梯度为0，参数不会更新，相当于隐藏层只有一个单元）
W1 = nn.Parameter(torch.randn(num_inputs, num_hiddens, requires_grad=True))
b1 = nn.Parameter(torch.zeros(num_hiddens, requires_grad=True))  # 向量
W2 = nn.Parameter(torch.randn(num_hiddens, num_outputs, requires_grad=True))
b2 = nn.Parameter(torch.zeros(num_outputs, requires_grad=True))   # 向量
params = [W1,b1,W2,b2]

# 2.实现 ReLu 激活函数
def relu(X):
    a = torch.zeros_like(X) # a的数据类型、形状都和X一样，但是元素值全为 0
    return torch.max(X,a)

# 3.实现模型
def net(X):
    #print("X.shape:",X.shape)
    # 原输入X：batch*28*28的 先拉成 batch*784
    X = X.reshape((-1, num_inputs)) #将输入X拉成一个二维矩阵，-1自动计算（结果应该为batch_size），（应该是以便可以满足X·W的矩阵乘法）
    #print("X.shape:",X.shape)
    H = relu(X @ W1 + b1) # @：矩阵乘法
    #print("H.shape:",H.shape)
    #print("W2.shape:",W2.shape)
    return (H @ W2 + b2)

# 损失
loss = nn.CrossEntropyLoss() # 交叉熵损失

# 4.【训练】多层感知机的训练过程与softmax回归的训练过程完全一样
num_epochs ,lr = 30, 0.1
updater = torch.optim.SGD(params, lr=lr)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, updater)

基于框架实现

和之前区别不大

import torch
from torch import nn
from d2l import torch as d2l
# 0.
batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

# 1.实现一个具有单隐藏层的多层感知机，它包含256个隐藏单元
num_inputs, num_outputs, num_hiddens = 784, 10, 256 # 输入784、输出10是数据决定的，256是调参自己决定的（超参数，选的是10-784之间的一个数）
# 初始化w1的行数为784、列数256。此处加不加nn.Parameter都行。
# 为什么此处要随机初始化randn，而不是全初始化为0？（弹幕说：设置为零的话梯度为0，参数不会更新，相当于隐藏层只有一个单元）
W1 = nn.Parameter(torch.randn(num_inputs, num_hiddens, requires_grad=True))
b1 = nn.Parameter(torch.zeros(num_hiddens, requires_grad=True))  # 向量
W2 = nn.Parameter(torch.randn(num_hiddens, num_outputs, requires_grad=True))
b2 = nn.Parameter(torch.zeros(num_outputs, requires_grad=True))   # 向量
params = [W1,b1,W2,b2]

# 2.实现 ReLu 激活函数
def relu(X):
    a = torch.zeros_like(X) # a的数据类型、形状都和X一样，但是元素值全为 0
    return torch.max(X,a)

# 3.实现模型
def net(X):
    #print("X.shape:",X.shape)
    # 原输入X：batch*28*28的 先拉成 batch*784
    X = X.reshape((-1, num_inputs)) #将输入X拉成一个二维矩阵，-1自动计算（结果应该为batch_size），（应该是以便可以满足X·W的矩阵乘法）
    #print("X.shape:",X.shape)
    H = relu(X @ W1 + b1) # @：矩阵乘法
    #print("H.shape:",H.shape)
    #print("W2.shape:",W2.shape)
    return (H @ W2 + b2)

# 损失
loss = nn.CrossEntropyLoss() # 交叉熵损失

# 4.【训练】多层感知机的训练过程与softmax回归的训练过程完全一样
num_epochs ,lr = 30, 0.1
updater = torch.optim.SGD(params, lr=lr)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, updater)

QA

1.下图中的两个x不是一个东西

2.【神经网络层数的说明】通常来讲，一层是指带权重的
一般来说，一层是包括【w、输入、b等权重的计算】+【（非线性）激活函数sigma的计算】的。
如吴恩达，一般将input不算层数， 是所有的隐藏层+output 层 = 层数（当然也能理解为 input+所有隐藏层 不算输出层，其实意思是一样的，只是一般 不算input层，算output层）

个人感觉看几层没有绝对的定论，只是比表述、描述方式不同
感觉也不一定,吴恩达说过几层有的是不包括输入层的,也就是看权重有几层.但在其他一些地方就包括了输入层,这个几层无伤大雅
【下图无论用哪种看法 看 都是两层】每个箭头相当于可以学习的权重

3.涉及数学上的统计学 与 机器学习的区别，
收敛定理是统计学中的概念

可以认为：统计是数学上的概念，那么 机器学习就是统计的计算机分支
因此 从计算机的角度，不会看ρ怎么算
数学和计算机是有关联得

4.从时间顺序上来说：多层感知机是在SVM之前出现的
多层感知机虽然解决了XOR问题，但是 其弊端是需要 选择、学习超参数；
但是SVM对于超参数不敏感， 最中间结果好坏受超参数影响很小。SVM的优化更容易实现（无需 SGD这种东西）。SVM有很漂亮的数学定理，有很多数学性的东西，如果 二者作用效果差不多 当然使用SVM。

现在之所以推荐用多层感知机MLP是因为，当问题变了后 你想改成别的神经网络，MLP的代码只需要简单修改、大体的优化算法等内容基本无修改 即可实现，而用SVM的改动量较大

5.无。单纯是为了 举证单层感知机解决不了的问题 而举的例子

6.是的。单层感知机不能处理

模型复杂度（模型容量）简单理解就是模型的能力。一般为了实现相同的模型复杂度，有两种修改思路： 用宽的网络（隐藏层数量不多，但是单个隐藏层中神经元个数多）或深的网络（隐藏层数量多）
但是，胖的模型（如下图左侧）不如 深的模型（下图中右侧）好训练，
胖的模型容易过拟合，很难一口吃成个胖子；
深的模型 通过每一层逐步学习，每层学习不同的特征，整体更好实现效果
（弹幕说）这个问题推荐看李宏毅老师的鱼和熊掌可以兼得那集，讲得很细

8.后面讲

9.ReLU虽然在x大于0或小于0部分都是线性的，但是整体上是非线性的。

10.选择激活函数的类型远远没有 选择隐藏层大小（即如隐藏层超参数的学习）重要，因此一般用ReLU即可

12.理论上没区别，但一般 深一点的更好。没有最优
一般来说，当你没有什么想法时：都是从简单慢慢试到复杂， 到更宽、更深。
如下图一开始就用线性模型，后来加一个隐藏层， 改变单个隐藏层的设计， 再增加多个隐藏层，再试着改变多个隐藏层中每一个的设计

当你有了自己的理解后： 手感、只可意会

13.后面讲

14.怎么写都没有本质区别，和你如何定义 矩阵、向量有关（比如矩阵是mxn还是nxm，向量是行还是列）

15.一般训练完 参数都是固定的。

动态性和泛化性（鲁棒性）是两种东西
一旦有动态性可能会出现问题（如谷歌将黑人预测为猩猩）。
泛化性（鲁棒性）：感觉就是 可靠准确的输出结果受 输入数据变化的影响程度，
泛化性低：比如 人脸识别时 换个姿势 就识别不准确了

弹幕说：其实，这个问题可以看看吴恩达机器学习的线上学习部分

17.后面讲

18.【即调参】可以用验证数据集做这个事情。 可以猜、试，然后用 数据去初试一下效果

11-模型选择（即选择超参数）+过拟合欠拟合

模型选择

引言

但其实 穿蓝衣服作为特征是无意义的，但是模型不知道。

训练误差和泛化误差、训练+验证+测试集

我们关心的是泛化误差，不关心训练误差（但也不是这么绝对，毕竟训练误差也能说明一些问题 给我们提供调整模型的指导意义）。

训练误差：高考前的模拟考试（摸底）
泛化误差：高考（ 模型在 目前不在手上的数据上的误差）

如何计算训练误差和泛化误差，一般我们有两种数据集
【训练（数据）集】
（1）用于训练模型参数
（2）通俗理解：平时作业题、练习。

【验证（数据）集 cv】
（1）是一个额外的数据集、不参加训练，用于选择模型超参数
（2）通俗理解：验证集是小测和模拟考试
（3）个人补充（QA中提到）：用validation set来看欠、过拟合情况

【测试（数据）集 test】相当于正式考试（期末考试、高考）只能使用一次，不能用来调整超参数，一旦发生了就不能改变了。（测试数据集是用来评估模型泛化能力的，不在训练过程中使用，只在结束后使用）

【注意】
1.验证数据集的数据一定不能和训练数据集混在一起
2.用测试数据集当作验证数据集去评估模型的好坏并调整超参数，然后再在测试数据集上看所谓的最终效果效果（那肯定很好），相当于考试作弊（学术造假）【此时在 验证数据集上的数据精度和指标 不能代表 该模型在 新的数据集（即测试集）上的泛化能力】
（弹幕说）测试数据集用一次，就是防止调参过程中无意识的去拟合测试数据，那么这样测试数据就成了训练数据了，测试没有意义了
【注】实际场景下 三个集肯定要单独分开的，此处课程为了方便 把验证集当成测试集了

K-则交叉验证（k-fold cross validation）（数据集不大时才用）

【引言】实际场景下，我们手中的数据量有限，无法做到 将 50%的数据用作训练集、50%用作验证集。
【作用】用来确定超参数
【应用】例如给你一个数据集，且 模型有10种不同的超参数（如不同的lr、不同隐藏层大小等）供选择，通过k则交叉验证（如5则）， 对每一种超参数对应的模型都 使用k则交叉验证并 最终得到该种超参数的 平均精度（或平均误差）， 从10个平均精度中选择最高的那组超参数作为最终的超参数。

个人理解：每组超参数通过k则交叉验证都能得到 一个平均精度

【使用流程】
1.拿到数据集后，将其随机打乱并分割成k块，然后做k次训练，
2.每次我们将第i块 作为验证数据集，其余的为训练数据集。这样这k次训练，每次都能拿到一个验证精度、验证误差，共k个
3.最后将这k个精度求平均值，就得到了k则交叉验证的误差
如下图3则：
相当于用了66%的数据作为train，虽然验证集validation不足之前的50%，但是 其带来的误差可以通过 求 3次的平均值来弥补

极端例子：k=n，n很大， 这样的代价就是需要做n次训练，代价很大
【k的取值】如果数据量很大，k可以取小点如2、3；如果数据量很大，k可以取大点，如10.

欠拟合、过拟合

概述

【深度学习的核心】首先是要模型足够大（不大的话没有前途，很难解决复杂问题），在此基础上通过各种手段 来控制模型容量，使得最终得到较小的泛化误差

模型容量即模型复杂度：拟合各种函数的能力。复杂的模型可以学习更复杂的函数。模型容量低就是简单的模型。
简单数据集如MNIST，复杂数据集如ImageNet

过拟合：过于关注细节，模型记住了所有的 训练样本，导致对新样本的泛化能力差
（某种意义上来说过拟合不是一件坏事）

模型容量（模型复杂度、模型能力）

模型容量即模型复杂度：拟合各种函数的能力。复杂的模型可以学习更复杂的函数。模型容量低就是简单的模型。

【深度学习的核心】首先是要模型足够大，在此基础上通过各种手段 来控制模型容量，使得最终得到较小的泛化误差

假设数据集是中等且固定的情况下：
目的是为了减小 最优的泛化误差，因此 不得不需要承担一定程度上的过拟合

横轴上每一个点都是不同的模型

估计模型容量

【1.参数个数】通过参数数量来判断模型容量
（1）对于线性模型（下图左侧）：可学习的参数个数为d+1（其中数据有d个，d+1的1是b（bias））
（2）对于单层隐藏层（下图右侧）：
隐藏层里有m个节点，每个节点包含d个w参数和一个bias参数，所以是(d+1)m
输出层最终预测为k个类别，输出层的每个y_hat节点包含m个w参数(由上一层的节点数决定)和一个bias，所以是(m+1)k
（3）结论：因此简单来说，可以通过 可学习的参数数量来 判断哪个模型容量大

【2.参数值的选择范围】通过参数值的可选择范围来判断模型容量
（1）如果一个参数可以在很大的范围内进行选择，模型复杂度高

【了解】VC维（偏统计学理论）

【简单理解】一个模型能记住的最大的数据集长什么样子
推荐《机器学习基石》林轩田老师对应的视频

深度学习中的VC维 计算较困难，在深度学习中应用不多

（两个大佬的首字母缩写）
VC维简称为VC：
对于一个分类模型，VC维等价于 一个最大的数据集的大小， 无论我们如何给定这个数据集的标号（即数据的label），都存在一个模型（一个给定参数的模型）能对该数据集进行完美分类。

简单理解：假设我的模型能做（作用于）一个很复杂的数据集，假设有100张图片，不管这些图片的label如何变化、不管图片中的值如何选择，我都可以通过一个模型对该数据集进行分类， 那么 该模型的复杂度 比 我只能对一个 10张图片、且不管label怎么变化都能分类的数据集 来得快。

模型复杂度等价于 我能够完美的记住一个数据集，那么这个数据集有多大。

例子：
如下图，对于二维输入的感知机（二维即平面上的点），其可以 对 任何三个点进行正确分类，则VC维=3；
但不能对任何四个点正确分类

数据复杂度

即我们直观上的理解

如有时间、空间维度上的数据、特征信息

基于代码看现象

基于代码看一下 模型选择、欠拟合过拟合的现象，通过一个简单的人工数据集：

参考链接：https://blog.csdn.net/weixin_46805040/article/details/122851333

0【公式】
① 使用以下三阶多项式来生成训练和测试数据的标签：
② 这个式子只是一个三次多项式，并不是哪个函数的泰勒展开。

公式中5为真实label；
除以2！和3！是希望x不要太大

4.模型net就是一个简单的线性回归模型（这个能很好地 演示 对于简单的模型，输入不同数量的数据时的效果）：
当给 正好的数据量时，拟合效果很好（如(5)）；
当给的数据太少时，欠拟合 如(6)；
当给全部的数据时，过拟合（因为 后面16列都是噪音，是干扰， 该模型为了拟合这些 学的结果肯定不对）

5.拟合很好的效果： 拿前4列数据（因为 后面16列理论上都是0，后面都是噪音）
下图 最终 的gap不大，说明没有发生很明显的过拟合

# 三阶多项式函数拟合(正态)
train(poly_features[:n_train,:4],poly_features[n_train:,:4],labels[:n_train],labels[n_train:])  # 最后返回的weight值和公式真实weight值很接近       

6.欠拟合效果：拿前两列来训练（数据都没给全，肯定 最后训练不到位）

# 一阶多项式函数拟合(欠拟合)
# 这里相当于用一阶多项式拟合真实的三阶多项式，欠拟合了，损失很高，根本就没降
train(poly_features[:n_train,:2],poly_features[n_train:,:2],labels[:n_train],labels[n_train:])

7.过拟合效果：
这次把所有数据（共20列）都给你了（含16列噪音）

# 十九阶多项式函数拟合(过拟合)
# 这里相当于用十九阶多项式拟合真实的三阶多项式，过拟合了
train(poly_features[:n_train,:],poly_features[n_train:,:],labels[:n_train],labels[n_train:])

【其他部分总代码】

# 通过多项式拟合来交互地探索这些概念
import math
import numpy as np
import torch
from torch import nn
from d2l import torch as d2l


# 0.
max_degree = 20 # 输入特征为20种（长度为20）：就是每一个样本是一个[20,1]的tensor
n_train, n_test = 100, 100 # 100个训练样本、100验证样本（即测试样本）  注：为了偷懒方便，将验证集也写为test
true_w = np.zeros(max_degree)  # 真实的w是长为20的w
true_w[0:4] = np.array([5,1.2,-3.4,5.6]) # 真实label为5，即只有前4列是有非0权重的，剩下其他元素的均为0，即噪音项

features = np.random.normal(size=(n_train+n_test,1))
print(features.shape)
np.random.shuffle(features)
print(np.arange(max_degree))
print(np.arange(max_degree).reshape(1,-1))
print(np.power([[10,20]],[[1,2]]))
poly_features = np.power(features, np.arange(max_degree).reshape(1,-1)) # 对第所有维的特征取0次方、1次方、2次方...19次方  
for i in range(max_degree):
    poly_features[:,i] /= math.gamma(i+1) # i次方的特征除以(i+1)阶乘
labels = np.dot(poly_features,true_w) # 根据多项式生成y，即生成真实的labels
labels += np.random.normal(scale=0.1,size=labels.shape) # 对真实labels加噪音进去

#1.看一下前两个样本
true_w, features, poly_features, labels = [torch.tensor(x,dtype=torch.float32) for x in [true_w, features, poly_features, labels]]                 
print(features[:2]) # 前两个样本的x
print(poly_features[:2,:]) # 前两个样本的x的所有次方
print(labels[:2])  # 前两个样本的x对应的y

# 2.实现一个函数来评估模型在给定数据集上的损失
def evaluate_loss(net, data_iter, loss):
    """评估给定数据集上模型的损失"""
    metric = d2l.Accumulator(2) # 两个数的累加器
    for X, y in data_iter: # 从迭代器中拿出对应特征和标签
        out = net(X)
        y = y.reshape(out.shape) # 将真实标签改为网络输出标签的形式，统一形式
        l = loss(out, y) # 计算网络输出的预测值与真实值之间的损失差值
        metric.add(l.sum(), l.numel()) # 总量除以个数，等于平均
    return metric[0] / metric[1] # 返回数据集的平均损失

# 3.定义训练函数（输入数据，做线性回归，打印看下曲线变化，看下学到的weight）
def train(train_features, test_features, train_labels, test_labels, num_epochs=400):
    loss = nn.MSELoss()
    input_shape = train_features.shape[-1]
    net = nn.Sequential(nn.Linear(input_shape, 1, bias=False)) # 单层线性回归
    batch_size = min(10,train_labels.shape[0])
    train_iter = d2l.load_array((train_features,train_labels.reshape(-1,1)),batch_size)
    test_iter = d2l.load_array((test_features,test_labels.reshape(-1,1)),batch_size,is_train=False)    
    trainer = torch.optim.SGD(net.parameters(),lr=0.01)
    animator = d2l.Animator(xlabel='epoch',ylabel='loss',yscale='log',xlim=[1,num_epochs],ylim=[1e-3,1e2],legend=['train','test'])                   
    for epoch in range(num_epochs):
        d2l.train_epoch_ch3(net, train_iter, loss, trainer)
        if epoch == 0 or (epoch + 1) % 20 == 0:
            animator.add(epoch + 1, (evaluate_loss(net, train_iter, loss), evaluate_loss(net,test_iter,loss)))
    print('weight',net[0].weight.data.numpy()) # 训练完后打印，打印最终学到的weight值  

QA

1
缺点：
（1）SVM是通过kernel来匹配模型复杂度的，.如果使用 kernel SVM，其kernel算起来麻烦， 很难计算大的数据量（如百万千万），但 神经网络 就可以算
（2）可调整的东西不多， 无非是kernel相关

神经网络的优点：
（1）神经网络本身是一种语言， 不同的layer（相当于编程工具），我们通过编程来实现我们对世界的理解
（2）神经网络可通过卷积进行特征的提取和分类，SVM解决分类问题还是ok的
（3）神经网络解决大量数据问题也可以

3.是的。

4.如1

常用方法：
（1）train :test=7:3，然后在trainset上做5则交叉验证（即每次拿训练集的20%作为验证集，做5次）
（2）如果数据量足够多，就 train:test= 5:5，在train set上做k则交叉验证
（3）如ImageNet，有1000类label，平均一个类大概5000张样本，对每个类随机挑50张图片，最后得到50000张的验证集，剩下的作为测试

注：Andrew Ng’s machine learning里推荐0.6 0.2 0.2

6.用validation来看欠、过拟合

7.如股票预测，时序序列需要保证验证集是在训练集之后的
不能这么做：将前一个月数据拿出来，中间采样一些点作为验证集
一般时序序列数据的做法：获取一个月数据作为训练集， 取一个星期作为验证集，该星期之前的作为训练集

当要做标准化时， 如(数据-均值)/方差，均值和方差如何计算：
方法一：把训练集和测试集（即所有的数据集）都拿过来算均值和方差（模型鲁棒性更好）
方法二：只在训练集上算均值、方差，然后将二者作用到验证（测试）集上

具体看实际场景下，你是否能拿到验证集的数据，如果能拿到，用方法一，拿不到就方法二

9.是的。深度学习一般数据量大，用k则交叉验证成本太大

10.验证集只是用来选择超参数的

11. 总的数据集就是一个， 然后将数据分成几份数据集，不同的数据集做不同的事情

12.理论上k越大 效果越好 但成本和代价越大，因此实际上 选择 能承受的计算成本范围内 选最大的k

13.不同。
模型参数指w权重、b偏差的值
超参数：如人为选择模型（是线性模型还是多层感知机 还是其他模型），如果是多层感知机 选多少层、每层多大， 训练的lr多少
个人概括：超参数就是人为可设置、人为可选的参数；模型参数就是 通过训练 模型自己得到的参数
hyperparameter

14.例如给你一个数据集，且 模型有10种不同的超参数（如不同的lr、不同隐藏层大小、不同权重等）供选择，通过k则交叉验证（如5则）， 对每一种超参数对应的模型都 使用k则交叉验证并 最终得到该种超参数的 平均精度（或平均误差）， 从10个平均精度中选择最高的那组超参数作为最终的超参数。

15.问的应该是偏差和方差的区别

16.欠过拟合能告诉你什么样是好的，什么样是不好的，供你参考 以便最后选择合适的超参数来 得到泛化能力好的模型

17.HPO问题：超参数优化，Hyper-parameter optimization
涉及到两个问题：
1.设计：例如前面的例子 设计了10组不同的超参数 从里面选一种， 那么这10种如何设计
2.每种超参数都告诉你有多少种选项，理论上 有很多种组合方式，但是很难把所有情况都遍历一次（此即为网格）

答：
超参数的设计靠人的经验，一般别的太大或太小
如何选最好的搜索：
1.自己调（老中医）
2.每次随机选，最后选 精度最高表现最好的那组超参数【推荐】

实际两类数据的占比是1:9：
当数据量很大时，随便划分比例都可；
当数据量不大时，验证数据集中两类数据最好比例1:1（因为 可能 分类器把所有样本都预测为 占比为9的那类，准确率还有90%，显然不合理）

19.k则交叉验证就是用来确定超参数
有很多种做法，此处举例：
1.最常见的：基于k则交叉验证确定表现最好的一组超参数，然后用该组超参数再训练一次模型，得到最后结果
2.不重新训练，直接选择该组超参数以及 该组超参数下的精度最好的那一则模型参数。（代价就是 少看了一些训练集）
3.（也不错的选择，好处是增加了模型稳定性 因为做了voting，代价是 预测代价是只预测一次的k倍）基于k则交叉验证选择好一组超参数后， 并 把 k则交叉验证的k个模型都拿到，做预测时 把测试集放到 k个模型的每个里面都预测一下，最后把预测结果取均值

20.验证误差 validation误差

21.不是打败，是流行

深度学习打败SVM是 实用性更好（虽然理论不如SVM）

22.网上的图 Loss和epoch的曲线，全程是一个模型，横轴是迭代次数；
下图的横轴是 代表不同的模型；

如果验证集上 loss和epoch的曲线 先下降后上升，就是过拟合

24.一般深度学习特指神经网络 这一块，随机森林和深度学习结合的 较少。一般可能是 用随机森林（不是用梯度下降的）、神经网络、其他方式各做一次，然后 对多种方式的结果投票得到最终结果

25.有的

26.label

27.一般深度学习模型 不做限制（如正则化、泛化等）都是无限VC维的

28.见19，有很多种方式

30.见19

31. CNN其实本质上也是MLP，只不过多了一些限制（比如将一些weight固定住了）
    即 通过神经网络来描述 我对这个问题的理解

世界上有三种东西：
艺术：我做了一件事，但我也不知道怎么解释，我觉得这样好看点
工程：我做的事情可以通过实际来验证，都可以通过定理来描述
科学：去理解为什么

深度学习（神经网络）一开始是艺术（我有个想法 且 也能work，得想个理由如何解释，虽然 暂时也不知道如何解释是最合理的），但只要你能work，总有人帮你找到理由去解释为何work（此即engineer的任务）
比如蒸汽机先出现，解释蒸汽机的原理的物理学知识是100年后才出来的，有一定的滞后性

32.看从哪个角度看
涉及统计学的优化
像大数定理

33. 噪音肯定越少越好。 此处只是为了讲解和演示才加了噪音

34.可以不平衡，但应该通过加权使得其平衡
以问题18举例：实际两类数据的占比是1:9，此时要结合实际场景看一下：
（1）是否在现实场景下，确实 这两类的占比也是如你 手头数据集这样的 占比是1:9，那你的目标就是 把90%做好，10%尽量做好，这倒没事
（2）如果 数据集这种1:9的比例是因为采样没做好（即 10%比例的那类 也是很有意义的时），应该把 10%数据的那类的权重提升，最简单的如 把 该类样本复制为9倍 或 在loss中为其提高权重

35.如果验证集上 loss和epoch的曲线 先下降后上升，就是过拟合