互信息的简单理解
在介绍互信息之前,首先需要了解一下信息熵的概念:所谓信息熵,是指信息论中对一个随机变量不确定性的度量,对于随机变量x,信息熵的定义为: H ( x ) = − ∑ x p ( x ) l o g p ( x ) H(x)=-\sum_xp(x)logp(x) H(x)=−x∑p(x)logp(x) 随机变量的熵越大,说明这个变量带给我们的信息越多。
互信息(MI,Mutual Information)表示两个变量之间相互依赖程度的度量,即知道随机变量X,对随机变量Y的不确定性减少的程度;也可以表达知道Y的情况下随机变量X的不确定性,互信息的计算跟两个随机变量的顺序没有关系。我们通过韦恩图来解释这件事,对于随机变量X、Y,有:
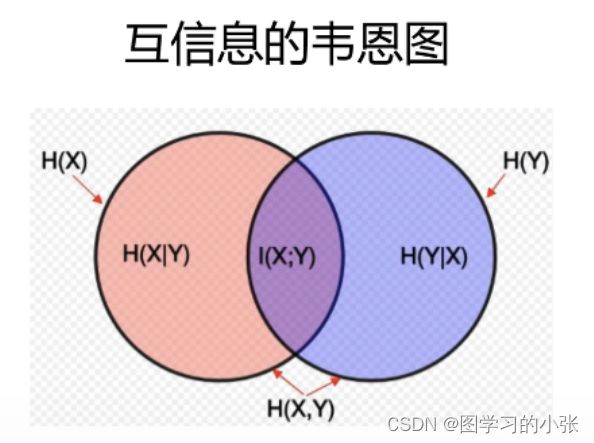
互信息定义为: I ( X , Y ) = H ( X ) − H ( X ∣ Y ) = H ( Y ) − H ( Y ∣ X ) = H ( X ) + H ( Y ) − H ( X , Y ) I(X,Y)=H(X)-H(X|Y)=H(Y)-H(Y|X)=H(X)+H(Y)-H(X,Y) I(X,Y)=H(X)−H(X∣Y)=H(Y)−H(Y∣X)=H(X)+H(Y)−H(X,Y)
带入信息熵、条件熵的公式并化简:
I ( X , Y ) = ∑ x , y p ( x , y ) l o g p ( x , y ) p ( x ) p ( y ) I(X,Y)=\sum_{x,y}p(x,y)log\frac {p(x,y)}{p(x)p(y)} I(X,Y)=x,y∑p(x,y)logp(x)p(y)p(x,y) 计算两个高维变量之间的互信息是很困难的,一般的,互信息可以写成KL散度(相对熵)的形式,即联合概率分布 p ( X Y ) p(XY) p(XY)与边际分布 p ( X ) p(X) p(X) P ( Y ) P(Y) P(Y)的乘积之间的KL散度: I ( X , Y ) = D K L ( P X Y ∣ ∣ P X P Y ) I(X,Y)=D_{KL}(P_{XY}||P_XP_Y) I(X,Y)=DKL(PXY∣∣PXPY) 由于计算高维变量间互信息的困难性,近年来有很多通过神经网络对互信息进行估计的方法,比较经典的一篇是MINE,过几天我会把这篇论文的笔记整理出来。