校门外的树--牛客网(第一次用结构体来解题)
题目描述
某校大门外长度为L的马路上有一排树,每两棵相邻的树之间的间隔都是1米。我们可以把马路看成一个数轴,马路的一端在数轴0的位置,另一端在L的位置;数轴上的每个整数点,即0,1,2,……,L,都种有一棵树。
由于马路上有一些区域要用来建地铁。这些区域用它们在数轴上的起始点和终止点表示。已知任一区域的起始点和终止点的坐标都是整数,区域之间可能有重合的部分。现在要把这些区域中的树(包括区域端点处的两棵树)移走。你的任务是计算将这些树都移走后,马路上还有多少棵树。
输入描述:
第一行有两个整数:L(1 <= L <= 10000)和 M(1 <= M <= 100),L代表马路的长度,M代表区域的数目,L和M之间用一个空格隔开。接下来的M行每行包含两个不同的整数,用一个空格隔开,表示一个区域的起始点和终止点的坐标。
输出描述:
包括一行,这一行只包含一个整数,表示马路上剩余的树的数目。
示例1
输入
复制500 3 150 300 100 200 470 471
500 3 150 300 100 200 470 471
输出
复制298
298
备注:
对于20%的数据,区域之间没有重合的部分; 对于其它的数据,区域之间有重合的情况。
一,嵌套循环,哈希表
1,思路
建立一个全为1的哈希表,遇到不能种树的区域,变为0,最后统计L中0出现次数。
#include
int main(){
int L,M;
scanf("%d %d",&L,&M);
int start,end;
int arr[10000]={0};
for(int i=0;i<=L;i++){
arr[i]=1;
}
for(int i=0;i 缺点,时间复杂度位O(种树区域长度*M),在最坏情况下,耗时很长,于是便有了下面的改进
2,思路
思路跟上面差不多,只是少了个赋值arr为1的情况
#include
int main(){
int L,M;
scanf("%d %d",&L,&M);
int arr[10001]={0};
int start,end;
for(int i=0;i<=L;i++){
scanf("%d %d",&start,&end);
for(int i=start;i<=end;i++){
arr[i]++;
}
}
int count=0;
for(int i=0;i<=L;i++){
if(arr[i]==0){
count++;
}
}
printf("%d",count);
return 0;
} 但是这样改,耗时还是很长,所以我们采用第二种算法
二,将有交集的数组合为一体
1,思路
将数据排序后分为有交集和没有交集两种情况
(1)有交集:
只要判断start2,与end1的大小,就能判断有没有交集,有的话就将此合为一体,就像代码里面写的,另y=end1与end2里面的较大值
(2)没有交集
只需用y(即为结束的值)减去x(开始的值),要注意多减去一,因为题目中说了,要包括两个端点
#include
#include
#include
struct A{
int start;
int end;
}arr[101];
int cmp( const void *a , const void *b )
{
struct A *c = (int *)a;
struct A *d = (int *)b;
if(c->start != d->start) return c->start - d->start;
else return d->end - c->end;
}
int main(){
int L,M;
scanf("%d %d",&L,&M);
for(int i=0;i 注意:在最后的时候,要再减一次,因为我们前面的循环,只涉及了前面m-1个数据
错误原因,我对结构体的qsort排序不太清楚,一直写成int的排序形式。
三,差分法
1,思路:
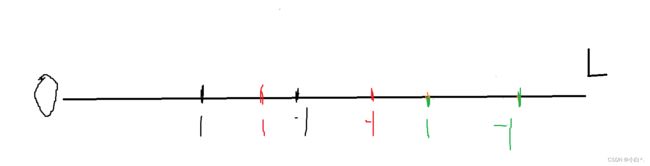
将种树的起点与结束位置,分别设置为1,和-1,如图所示不在1~-1区间内的即为要种树的,可以用一个变量a来记录,如果a从0变为1,则是种树区间,否则则不是,由于给出数据的大小不确定,所以我们要对其进行排序。代码如下
#include
#include
struct A {
int pos;
int number;
}arr[101];
int cmp(const void* p1, const void* p2) {
struct A* a = (int*)p1;
struct A* b = (int*)p2;
if (a->pos == b->pos)
return b->number > a->number;
else
return a->pos > b->pos;
}
int main() {
int L, M;
scanf("%d %d", &L, &M);
int x, y;
for (int i = 0; i < M; i++) {
scanf("%d %d", &x, &y);
arr[i].pos = x;
arr[i].number = 1;
arr[i + M].pos = y + 1;//根据题目要求,马路的端点也不能种树
arr[i + M].number = -1;
//关于为什么+M,实则是因为,i~M的数据都会别x起始位置占据
}
qsort(arr, 2 * M, sizeof(arr[0]), cmp);
int count = 0, a = 0;
int i = 0;
for (i = 0; i < 2 * M; i++) {
a += arr[i].number;
if (a == 1 && arr[i].number == 1) {//出现标记不中树木的情况时
count += arr[i].pos - arr[i - 1].pos;
}
}
count += (L - arr[2 * M - 1].pos + 1);
printf("%d", count);
return 0;
} 好多细节,代码中已经给出注释,我就来讲讲cmp函数这样构造的原因吧。
我们要注意到,某个点的起始位置与终止位置重合时候,由于题目要求该点不能种树,所以不能记这个点为种树区,所以我们可以先判断,当位置相同时侯,先把-1给出来,这样就不会把点记进去了。
还有一个要注意的就是末尾,他只记录了前2*M-1区域,所以要加上后面的种树区域.