MIT_线性代数笔记：第 29 讲 奇异值分解

本讲介绍奇异值分解（Singular value decomposition），简称 SVD。这是矩阵最终也是最好的分解，任意矩阵可分解为 $A=U\Sigma V^T$，分解结果为正交矩阵 U，对角阵Σ和正交矩阵 V。

如果矩阵 A 是正定矩阵，它的奇异值分解就是 $A=Q\Lambda Q^T$，一个正交矩阵 Q 就可以满足分解，而不需要两个。而对于可对角化的矩阵有 $A=S\Lambda S^{-1}$，但特征向量矩阵 S 并不是正交矩阵，而 SVD 中的 U 和 V 都是正交矩阵。

如何实现

可以将矩阵 A 视为一种线性变换操作，将其行空间中的一个向量 $v_1$,变为其列空间中的向量 $u_1=A{v}_1$。奇异值分解就是要在行空间中寻找一组正交基，将其通过矩阵 A 线性变换生成列空间中的一组正交基 $A{v}_i={\sigma }_i{u}_i$。

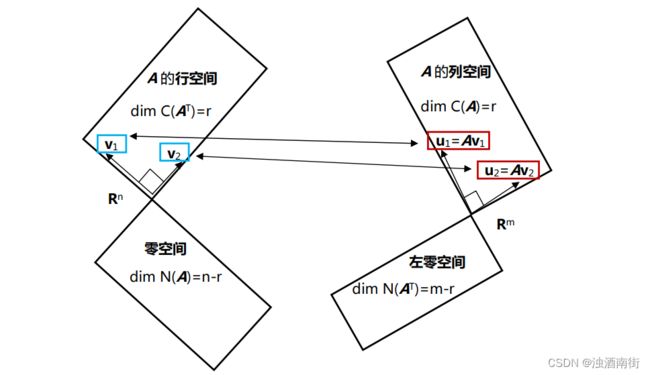
找出矩阵A行空间中的正交基很容易，Gram-Schmidt正交化过程就可以做到，但是随便的一组正交基经过矩阵矩阵 A 变换得到的向量并不一定正交，因此满足此要求的行空间的正交基非常特殊。而矩阵 A 零空间的向量所对应的是矩阵Σ 对角线上的 0 元素，因此很容易处理。

用矩阵数学语言描述这一过程

问题的核心就是找到行空间中一组特殊的正交基：

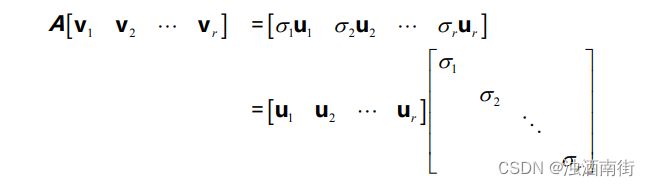
如果加入零空间的部分，等式就变为AV=UΣ。其中零空间对应的正交基$v_{r+1}\dots \dots v_n$，经过线性变换得到 Av=0，对应 矩阵中对角线最后的特征值${\sigma }_{r+1}={\sigma }_{r+2}=\dots =0$。在等式 AV=UΣ两侧右乘 V-1得到 $A=U\Sigma V^{-1}=U\Sigma V^T$。

现在的问题就是怎么找到符合要求的向量 $v_i和u_i$。 为了得到这两个正交矩阵，考虑首先解决其中的一个，在等式 $A=U\Sigma V^T$ 两侧分别乘上等式 $AT=V{\Sigma }^T{U}^T$两侧的项：

上式其实是正定矩阵 $A^{T}A$的正交分解，$v_i$就是矩阵 $A^{T}A$ 的特征向量，${\sigma }_i^2$就是矩阵 $A^{T}A$ 的特征值，奇异值${\sigma }_i$要取正平方根。用同样的办法也可以求得 U，它的列向量就是矩阵 $A{A}^T$的特征向量。

举例

例 1：矩阵 $A=\left[\begin{array}{cc}4& 4\\ -3& 3\end{array}\right]$ ，求其 SVD 分解。
矩阵为可逆矩阵，秩为 2，则需要在行空间中求得 $v_1$，$v_2$，列空间中求得 $u_1$，$u_2$，以及伸缩因子${\sigma }_1$，${\sigma }_2$。

计算$A^{T}A=\left[\begin{array}{cc}4& -3\\ 4& 3\end{array}\right]\left[\begin{array}{cc}4& 4\\ -3& 3\end{array}\right]=\left[\begin{array}{cc}25& 7\\ 7& 25\end{array}\right]$,它的特征向量为$\left[\begin{array}{c}1\\ 1\end{array}\right]$ 和$\left[\begin{array}{c}1\\ -1\end{array}\right]$。标准化得到$v_1=\left[\begin{array}{c}\frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}\end{array}\right],v_2=\left[\begin{array}{c}\frac{1}{\sqrt{2}}\\ \frac{-1}{\sqrt{2}}\end{array}\right]$,，求得${\sigma }_1^2=32$，${\sigma }_2^2=18$

求 U 的过程可以利用矩阵 $A{A}^T$。
$A{A}^T=\left[\begin{array}{cc}4& 4\\ -3& 3\end{array}\right]\left[\begin{array}{cc}4& -3\\ 4& 3\end{array}\right]=\left[\begin{array}{cc}30& 0\\ 0& 18\end{array}\right]$，求得${\sigma }_1^2=32$，${\sigma }_2^2=18$，它的特征向量为$\left[\begin{array}{c}1\\ 0\end{array}\right]$ 和 $\left[\begin{array}{c}0\\ 1\end{array}\right]$。

但是我们直接将 $\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]$作为矩阵 U 代入，会产生错误 $U\Sigma V^T=\left[\begin{array}{cc}4& 4\\ 3& -3\end{array}\right]$ 。这是因为确定特征向量的过程中，特征向量反向仍然符合要求，通过现在的方法无法确认向量的符号，但是一旦我们确认 v 的方向之后，u 的方向也就随之确定，将 v 代入 AV=UΣ 计算 u 可以避免这种问题。u 和 v 之间的符号联系在进行 $A{A}^T$的计算时被切断了，而用 AV=UΣ 可以避免此问题。

例 2：奇异阵 $A=\left[\begin{array}{cc}4& 3\\ 8& 6\end{array}\right]$，求其 SVD 分解。
矩阵的秩为 1，行空间和列空间都是 1 维的。行空间和零空间可以找到一组正交基转换得到列空间和左零空间的一组正交基。

很容易确定$v_1=\left[\begin{array}{c}0.8\\ 0.6\end{array}\right],v_2=\left[\begin{array}{c}0.6\\ -0.8\end{array}\right],u_1=\frac{1}{\sqrt{5}}\left[\begin{array}{c}1\\ 2\end{array}\right],u_2=\frac{1}{\sqrt{5}}\left[\begin{array}{c}2\\ -1\end{array}\right]$
$A{A}^T=\left[\begin{array}{cc}4& 8\\ 3& 6\end{array}\right]\left[\begin{array}{cc}4& 3\\ 8& 6\end{array}\right]=\left[\begin{array}{cc}80& 60\\ 60& 45\end{array}\right]$，秩 1 矩阵，很容易求得${\sigma }_1^2=125$，${\sigma }_2^2=0$

矩阵的 SVD 分解为：$A=\frac{1}{\sqrt{5}}\left[\begin{array}{cc}1& 2\\ 2& -1\end{array}\right]\left[\begin{array}{cc}\sqrt{125}& 0\\ 0& 0\end{array}\right]\left[\begin{array}{cc}0.8& 0.6\\ 0.6& -0.8\end{array}\right]$。

做奇异值分解就是在矩阵的四个子空间中寻找到合适的基：
$v_1，v_2\dots \dots v_r$为行空间的标准正交基。
$u_1，u_2\dots \dots u_r$为列空间的标准正交基。
$v_{r+1}，v_{r+2}\dots \dots v_n$为零空间的标准正交基。
$u_{r+1}，u_{r+2}\dots \dots u_m$为左零空间的标准正交基。

奇异值分解在最小二乘法问题中有重要应用，因为在实际问题中常碰到矩阵 A不是列满秩的状态，因此 $A^{T}A$ 不可逆，无法用之前的方法求最优解。即使是列满秩的情况当矩阵是超大型矩阵时，$A^{T}A$ 的计算量太大，用奇异值分解的办法会降低计算量。