机器学习周记（第二十七周：文献阅读-EIGRN）2024.1.22~2024.1.28

目录

摘要

ABSTRACT

1 论文信息

1.1 论文标题

1.2 论文摘要

1.3 论文背景

2 论文研究

2.1 问题描述

2.2 基准模型

2.3 论文模型

3 模型模块

3.1 图生成（graph generation）

3.1.1 显式图生成模块（explicit graph generation module）

3.1.2 隐式图生成模块（implicit graph generation module）

3.2 邻居聚合（neighbor aggregated）

3.3 时空信息融合（spatio-temporal information fusion）

3.4 预测模块（prediction modules）

---

摘要

  本周阅读了一篇通过时空图神经网络作为基准模型实现时间序列缺失值插补的论文。论文模型通过融合基于先验知识的图结构信息（显式图，静态图）和基于节点嵌入图学习的图结构信息（隐式图，动态图），能够适配任何时间序列的缺失值插补。同时该模型不仅参考了正向的时间序列信息，还参考了反向时间序列信息，充分利用时间序列中的有效值，增强了插补值对多元时间序列关系依赖影响中的真实性。

ABSTRACT

This week, We read a paper on time series imputation using a spatio-temporal graph neural network as a baseline model. The model in the paper achieves imputation of missing values in time series by integrating graph structure information based on prior knowledge (explicit graph, static graph) and graph structure information based on node embeddings graph learning (implicit graph, dynamic graph). This enables the model to adapt to missing value imputation for any time series. Additionally, the model not only considers forward time series information but also incorporates backward time series information, effectively utilizing valid values within the time series. This enhances the authenticity of imputed values in capturing dependencies in multivariate time series relationships.

1 论文信息

1.1 论文标题

Exploring explicit and implicit graph learning for multivariate time series imputation

1.2 论文摘要

  由于数据录入错误、设备损坏、数据传输过程中丢包等原因，多元时间序列会存在缺失值。想要完成时间序列数据分析任务在很大程度上依赖于缺失值填充这一基本任务。缺失值填补技术通常忽略了时间序列变量间的关系。尽管一些基于图的算法可以捕获这些关系，但图结构的设计通常是人为设计的，并且以数据集为中心。本文提出一种新的显式和隐式图循环网络（EIGRN），用于多元时间序列填补，集成了图和循环神经网络，一起捕获变量和时间依赖。主要的原理是通过有效地集成外部数据源（如先验知识和节点之间的隐式关系）来实现的。为了使论文的方法更适用于缺失值数量较多的数据集，作者还讨论了模型在不同缺失值比例下的性能。在真实数据集上的多方面实验表明，所提出模型在不同的应用领域优于最先进的模型。

1.3 论文背景

  多元时间序列（MTS）是指由跨多个变量的时间对齐序列组成的数据类型。时间序列广泛存在于各个领域，如金融市场、交通流量管理和工业系统。时间序列在处理这些领域方面发挥着重要作用，因为它不仅描述了单个变量的演变趋势，而且还捕获了这些变量之间的相互依赖关系。缺失值给MTS任务带来了长期的挑战。然而，由于多种影响因素，缺失值的出现实际上是不可避免的。例如，真实的工业生产环境往往使用多种传感器监测和生产线控制仪器，由于各种因素，例如硬件故障、连接丢失和存储错误，从这些传感器收集到的数据普遍不完整。在几乎所有的研究中，缺失的值都可能会导致各种问题，并严重影响从数据中得出的结论。例如，在任何旨在从数据中学习的机器学习模型中，缺失的值都会导致参数估计的偏差，降低从数据中得出令人信服的结论所必需的统计能力。在极端情况下，它们可能会扭曲整个数据，威胁到试验的有效性，从而导致完全无用的结论。

  为减轻缺失值对时间序列相任务的不利影响，目前已经存在了一系列相关的研究。处理缺失值最直接方法是简单地忽略缺失值——在这种情况下，只使用剩余的数据集进行分析。虽然这种策略很方便，但由于可能无意中从时间序列中消除了基本变量，从而使得整个数据产生很少的信息。在缺失观测的百分比高于80%的特殊情况下，简单地删除缺失值可能会导致严重的信息丢失，这可能不利于后续的数据处理任务，如分类和预测等。此外还有插补方法，其目的不是去除缺失数据，而是根据时间序列中可用的观测值来填充缺失数据。该方法有可能获得与原始（无损）数据相似的数据集，因此近年来吸引了越来越多的关注。

  现有的MTS填补方法通常分为三类，即基于统计的方法、基于机器学习的方法和基于深度学习的方法。统计方法往往过于简单，无法发现数据中的复杂模式，虽然机器学习方法可以探索数据的复杂性，但它在建模之初往往太过依赖于假设，当数据不满足这些假设时，模型的性能将显著下降。随着深度学习的发展，越来越多的工作致力于研究深度学习模型，尤其是循环神经网络（RNNs）和图神经网络（GNNs），作为解决多元时间序列填补任务的基础框架。基于RNN的模型通常根据有限的观测值迭代调整其隐藏状态，以捕获时间依赖性，从而促进缺失值的填补。然而，它只关注于重构特定于时间的依赖关系，而忽略了变量关系的重要性。相比之下，基于GNN的方法可以捕捉变量水平上的空间关系。大多数相关研究使用带有外部信息的预定义图结构，无法捕捉其中变化的变量依赖关系，也不能很好地泛化到各个工业领域的数据集。尽管旨在通过从可用的观察值中自适应地学习图结构来捕获潜在的变化变量依赖关系的努力也是有限的，而且缺乏对于外部信息（例如显式图）的使用。

  鉴于上述目前研究的局限性，本文提出动态学习潜在的变量间依赖关系，以补充捕捉变量间显式关系的外部信息。受GNN在传统任务时间序列预测中的成功启发，采用图结构来表示变量关系。尽管基于图的方法已被广泛应用于MTS预测，但时间序列插补的研究相对较少。本文清楚地区分了时间序列填补和预测任务。首先，时间序列插补侧重于数据重建和表示学习，通常是应用预测方法之前的准备步骤。其次，由于缺失值的位置通常是未知的，这要求填补方法不仅要沿着时间序列向前检查，还要向后检查，以充分利用不同时间戳的所有可用数据，以最大化填补性能。这意味着预测方法可能不容易适用于填补任务——即使直接应用是可行的，性能也会受到预测模型设计目标不一致的限制。预测任务和插补任务之间的直观比较如图1所示。遵循上述思想，本文提出一种显式和隐式图循环网络（EIGRN），用于捕获时间序列数据表面上和表面下对变量和时间敏感的依赖关系，用于MST填补。这种方法超越了仅依赖预定义图的传统方法，以更全面的方法来支持填充缺失值。

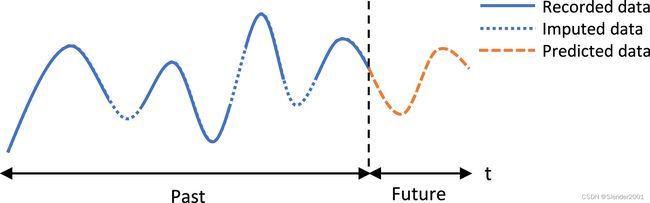Fig.1 时间序列插补与预测的不同

2 论文研究

2.1 问题描述

  多元时间序列插补是对历史记录中的缺失值进行预测。用和表示输入训练数据，其中上标表示序列，下标表示时间。与预测任务不同，所有时间戳都可以用于插补任务的训练。掩码矩阵与输入数据相同维度，表示时间序列中缺失值的位置，其中表示值缺失，否则，。任务的输出具有精确的尺寸并填充了所有缺失值作为下级任务的输入。因此，多元时间序列填补的任务旨在确定最接近底层真实值的值来填补中的缺失值。

2.2 基准模型

  论文通过图来表示所有变量之间的关系，其中和分别是节点和边的集合。用来表示图中节点的数量。对于一条边，可以表示为一个有序元组，即从节点到节点的边。论文将表示为根据先验知识构建的能够表示时间序列关系的显式图，将表示为从可训练的节点嵌入中学习的隐式图。显式图和隐式图的节点表示每个序列。整个图之间连通性的数学表示是邻接矩阵，其中是节点的数量，等于数据集中的变量数量。如果那么，反之如果则。从图的角度来看，论文描述时间序列之间的关系使用的是邻接矩阵。因此，带显式图和隐式图的多元时间序列插补任务可以被定义为：

                                                                                          （1）

表示论文模型中所有可学的参数，表示没有缺失值的真实值，表示论文模型的预测值，表示输入模型的包含缺失值的时间序列，是损失函数。

2.3 论文模型

  论文所提出的模型（如Fig.2所示）由四个部分组成：图生成（graph generation）、邻居聚合（neighbor aggregated）、时空信息融合（spatio-temporal information fusion）和预测模块（prediction modules）。它的工作原理如下：首先，图生成模块利用节点嵌入和距离信息生成表示变量关系的隐式图和显式图；然后，邻居聚合模块通过结合原始输入和图的邻接矩阵来生成具有邻居信息的聚合节点表示；接着，时空信息融合模块采用GRU进行时间信息传递；最后，预测模块融合前向分支和后向分支的输出完成最终的缺失值填补。

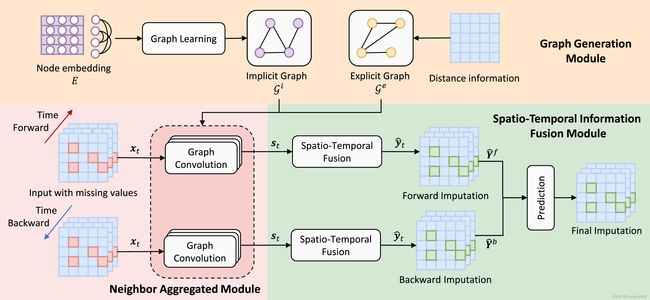Fig.2 论文模型的总体架构

3 模型模块

3.1 图生成（graph generation）

  该模块旨在使用空间图表示序列之间的关系。这些图随后将作为下级模块中的输入，促进特征表示的生成。

3.1.1 显式图生成模块（explicit graph generation module）

  显式图生成模块旨在捕获与外部领域知识相关的显式变量关系。论文使用传感器地理距离信息来表示变量之间的空间依赖关系。这种计算方法的基础假设是，位于地理距离较近的传感器比位于相距较远的传感器具有更高的相似性。论文使用带有阈值的高斯核来生成一个具有传感器之间地理距离的显式图。显式图的邻接矩阵可以通过以下公式计算：

                                                                             （2）

是中第个和第个节点之间边的权重，是距离计算公式，控制核的宽度，是阈值。在论文的实验中，作者将设置为数据集地理距离的标准差。是控制邻接矩阵密度的超参数。

3.1.2 隐式图生成模块（implicit graph generation module）

  隐式图生成模块是一种数据驱动的方法，旨在捕获隐式变量关系。另一种被广泛认可的用于捕获时间序列中节点关系的方法是注意力模块。值得注意的是，与注意力模块不同，图的邻接矩阵是稀疏的，可以被视为过滤第一层邻居信息的严格控制门。因此，dropout层对于隐式图生成至关重要，需要仔细设计。受许多强化学习工作的启发，论文使用Gumble Softmax来实现dropout层。该方法可以有效降低邻接矩阵的密度，降低后续模块的计算复杂度。隐式图的邻接矩阵可以用下面的公式计算：

                                                                                                                          （3）

是中第个到第个节点之间的边的权重。表示节点嵌入，是可学习的模型参数，是节点数量，是嵌入维度。对所有的，做。是温度系数，当时，，且其概率为，否则为。是sigmoid激活函数。是概率矩阵，是保持边从节点到的概率。在之前的研究中，可以很容易知道Gumbel Softmax与常规的Softmax具有相同的概率分布，这使得论文的图生成模块与概率矩阵生成一致。

3.2 邻居聚合（neighbor aggregated）

  给定来自前一个图生成模块的两个图（显式图和隐式图），论文将时间具有缺失值的输入序列与其相应的邻居信息合并，以生成一个潜在的聚合变量表示。具体来说，邻居聚合模块由层构建，公式表示为：

                                                                                                       （4）

其中和是时间的输入序列和掩码矩阵，是后续时空信息融合模块在时刻的隐藏状态，与Eq.5一致，是图邻接矩阵，是第层在时刻的聚合节点表示，是拼接操作。在论文的实验中，是一个由一维卷积层实现的特征融合函数。在接收到使用隐式图和显式图的两个聚合表示后，采用由多层感知器层实现的表示融合机制。这种融合过程将两种表示进行融合，使其有利于后续的时间信息学习。

3.3 时空信息融合（spatio-temporal information fusion）

  时空信息融合模块从图卷积模块接收来自前一个时间步长的隐藏状态，其聚合节点表示当前时间步长的。该模块结合两个信息流，在时间生成当前隐藏状态。在之前的研究之后，论文应用GRU来控制来自之前时间步骤的信息比例。隐藏状态的更新过程可以用如下公式表述：

                                                                                          （5）

其中和是重置门和更新门，是哈达玛积。和分别是sigmoid和双曲正切激活函数。因此，可以更新时刻的隐藏状态，并用于下一个时间步的计算。在完成个时间步的所有计算后，论文将和融合以生成分支的最终插补。

3.4 预测模块（prediction modules）

  受用于顺序数据处理的RNN的启发，本文引入了一种双向结构来结合前向和后向信息。与单向模型相比，后向分支可以整合来自未来时间步的信息，从而提高填补性能。最后的填补由前向和后向分支的输出组合得到，公式为：

                                                                                                                   （6）

其中是在时刻的重构向量，分别是前向和后向分支的填补序列，是表示缺失值位置的掩码矩阵，是最终的填补结果。是特征融合函数，与公式(4)一致，在论文的实验中由一维卷积层实现。论文定义多元时间序列插补的损失如下：

                                                                           （7）

其中和是和的逻辑二进制补码；和是中缺失值的重构数据；和是中缺失点的真值，是标准点积。在论文的实验中，是通过平均绝对误差实现的误差函数。