空间轴对称应力分析
本文继应力应变基础理论分析之后,探讨关于轴对称问题的理论分析。
在求解轴对称问题时,通常都采用圆柱坐标 r、 θ \theta θ、z。r是点P与Z轴的距离, θ \theta θ是通过Z轴及点P所作平面与xoz平面所成的夹角,z为对称轴。由于在轴对称问题中,各处的应力、应变和位移分量都对称于z轴,这些物理量只是r和z的函数,不随 θ \theta θ变化,所以采用圆柱坐标比直角坐标要方便得多。
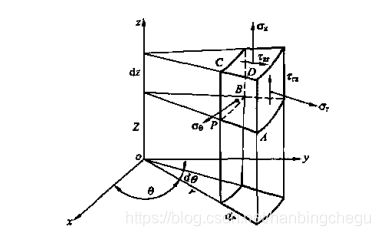
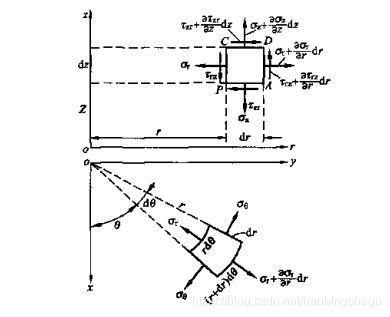
现在先讨论空间轴对称问题的平衡微分方程:如图,在物体内点P处取一微元六面体,六面体由两个半径差为dr的圆柱面、两个夹角为d θ \theta θ且包含x轴的垂直面和两个相距为dz的水平面所围成。
微元体六个面上的应力如上图所示:
- 沿着半径r方向的正应力记为 σ r σ_r σr,称为径向正应力;
- 沿圆周方向(环向)的正应力记为 σ θ \sigma_{\theta} σθ,称为环向正应力;
- 沿z轴方向的正应力,记为 σ z \sigma_z σz,称轴向正应力;
- 在圆柱面上,沿着z轴方向的剪应力,记为 τ r z \tau_{rz} τrz;
- 在垂直于z轴的水平面上且沿r方向的剪应力,记为 τ z r \tau_{zr} τzr,根据剪应力互等定理, τ z r \tau_{zr} τzr= τ r z \tau_{rz} τrz;
- 由于对称性,在包含z轴的平面上(如上图PADC面)无剪应力,则 τ θ r \tau_{\theta r} τθr= τ θ z \tau_{\theta z} τθz=0;
- 由于剪应力互等定理,可知: τ r θ \tau_{ r\theta} τrθ= τ θ r \tau_{\theta r} τθr=0, τ r θ \tau_{r\theta } τrθ= τ θ z \tau_{\theta z} τθz=0。
这样,在空间轴对称问题中,对于任意一点P,只有四个独立的应力分量,即 σ r σ_r σr、 σ θ σ_\theta σθ、 σ z σ_z σz 、 τ z r \tau_{zr} τzr= τ r z \tau_{rz} τrz。现用应力矩阵{σ}来表示这些应力分量,则有:
σ = { σ r σ θ σ z τ z r } (1) {σ}=\begin{Bmatrix} σ_r\\ σ_\theta \\σ_z\\\tau_{zr} \end{Bmatrix}\tag1 σ=⎩⎪⎪⎨⎪⎪⎧σrσθσzτzr⎭⎪⎪⎬⎪⎪⎫(1)
我们假设应力合力为 p p p,则:
{ ∂ p ∂ r = ∂ σ r ∂ r + ∂ τ z r ∂ z + σ r − σ θ r ∂ p ∂ z = ∂ σ z ∂ z + ∂ τ r z ∂ r + τ r z r (2) \begin{cases} \frac{\partial p}{\partial r}=\frac{\partial \sigma_r}{\partial r}+\frac{\partial \tau_{zr}}{\partial z}+\frac{\sigma_r-\sigma_\theta}{r}\\[1.5ex] \frac{\partial p}{\partial z}=\frac{\partial \sigma_z}{\partial z}+\frac{\partial \tau_{rz}}{\partial r}+\frac{\tau_{rz}}{r} \end{cases}\tag2 ⎩⎨⎧∂r∂p=∂r∂σr+∂z∂τzr+rσr−σθ∂z∂p=∂z∂σz+∂r∂τrz+rτrz(2)
其应变矩阵为:
ε = { ε r ε θ ε z γ z r } = { ∂ u ∂ r u r ∂ w ∂ z ∂ w ∂ r + ∂ u ∂ z } (3) \varepsilon=\begin{Bmatrix} \varepsilon_r\\ \varepsilon_\theta \\ \varepsilon_z\\ \gamma_{zr} \end{Bmatrix}= \begin{Bmatrix} \frac{\partial u}{\partial r}\\[1.2ex] \frac u r \\[1.2ex] \frac{\partial w}{\partial z}\\[1.2ex] \frac{\partial w}{\partial r}+\frac{\partial u}{\partial z} \end{Bmatrix}\tag3 ε=⎩⎪⎪⎨⎪⎪⎧εrεθεzγzr⎭⎪⎪⎬⎪⎪⎫=⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧∂r∂uru∂z∂w∂r∂w+∂z∂u⎭⎪⎪⎪⎪⎬⎪⎪⎪⎪⎫(3)
其中,
由上图,应力应变关系为:
{ ε r = 1 E [ σ r − μ ( σ θ + σ z ) ] ε θ = 1 E [ σ θ − μ ( σ r + σ z ) ] ε z = 1 E [ σ z − μ ( σ r + σ θ ) ] γ z r = τ z r G (4) \begin{cases} \varepsilon_r=\frac{1}{E}[\sigma_r-\mu(\sigma_\theta+\sigma_z)]\\[1.2ex] \varepsilon_\theta=\frac{1}{E}[\sigma_\theta-\mu(\sigma_r+\sigma_z)]\\[1.2ex] \varepsilon_z=\frac{1}{E}[\sigma_z-\mu(\sigma_r+\sigma_\theta)]\\[1.2ex] \gamma_{zr}=\frac{\tau_{zr}}{G} \end{cases}\tag4 ⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧εr=E1[σr−μ(σθ+σz)]εθ=E1[σθ−μ(σr+σz)]εz=E1[σz−μ(σr+σθ)]γzr=Gτzr(4)
将应力转变为应变的函数:
{ σ r = E ( 1 − μ ) ( 1 + μ ) ( 1 − 2 μ ) ( ε r + μ 1 − μ ε θ + μ 1 − μ ε z ) σ θ = E ( 1 − μ ) ( 1 + μ ) ( 1 − 2 μ ) ( ε θ + μ 1 − μ ε z + μ 1 − μ ε r ) σ z = E ( 1 − μ ) ( 1 + μ ) ( 1 − 2 μ ) ( ε z + μ 1 − μ ε r + μ 1 − μ ε θ ) τ z r = G γ z r = E 2 ( 1 + μ ) γ z r (5) \begin{cases} \sigma_r=\frac{E(1-\mu)}{(1+\mu)(1-2\mu)}(\varepsilon_r+\frac\mu{1-\mu}\varepsilon_{\theta}+\frac\mu{1-\mu}\varepsilon_z)\\[1.2ex] \sigma_\theta=\frac{E(1-\mu)}{(1+\mu)(1-2\mu)}(\varepsilon_\theta+\frac\mu{1-\mu}\varepsilon_z+\frac\mu{1-\mu}\varepsilon_r)\\[1.2ex] \sigma_z=\frac{E(1-\mu)}{(1+\mu)(1-2\mu)}(\varepsilon_z+\frac\mu{1-\mu}\varepsilon_r+\frac\mu{1-\mu}\varepsilon_\theta)\\[1.2ex] \tau_{zr}=G\gamma_{zr}=\frac E{2(1+\mu)}\gamma_{zr} \end{cases} \tag5 ⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧σr=(1+μ)(1−2μ)E(1−μ)(εr+1−μμεθ+1−μμεz)σθ=(1+μ)(1−2μ)E(1−μ)(εθ+1−μμεz+1−μμεr)σz=(1+μ)(1−2μ)E(1−μ)(εz+1−μμεr+1−μμεθ)τzr=Gγzr=2(1+μ)Eγzr(5)
根据 σ = D ε \sigma=\mathbf D\varepsilon σ=Dε,将上式整理成矩阵形式:
D = E ( 1 − μ ) ( 1 + μ ) ( 1 − 2 μ ) [ 1 μ 1 − μ μ 1 − μ 0 μ 1 − μ 1 μ 1 − μ 0 μ 1 − μ μ 1 − μ 1 0 0 0 0 1 − 2 μ 2 ( 1 − μ ) ] (6) \mathbf D=\frac{E(1-\mu)}{(1+\mu)(1-2\mu)} \begin{bmatrix} 1&\frac\mu{1-\mu}&\frac\mu{1-\mu}&0\\ \frac\mu{1-\mu}&1&\frac\mu{1-\mu}&0\\ \frac\mu{1-\mu}&\frac\mu{1-\mu}&1&0\\ 0&0&0&\frac{1-2\mu}{2(1-\mu)}&\\ \end{bmatrix}\tag6 D=(1+μ)(1−2μ)E(1−μ)⎣⎢⎢⎢⎡11−μμ1−μμ01−μμ11−μμ01−μμ1−μμ100002(1−μ)1−2μ⎦⎥⎥⎥⎤(6)
设体积应变为 e e e,则:
e = ε r + ε θ + ε z = ∂ u ∂ r + u r + ∂ w ∂ z (7) e=\varepsilon_r+\varepsilon_\theta+\varepsilon_z=\frac{\partial u}{\partial r}+\frac{u}{r}+\frac{\partial w}{\partial z}\tag7 e=εr+εθ+εz=∂r∂u+ru+∂z∂w(7)
式(5)可以整理为:
{ σ r = E μ ( 1 + μ ) ( 1 − 2 μ ) e + E 1 + μ ∂ u ∂ r σ θ = E μ ( 1 + μ ) ( 1 − 2 μ ) e + E 1 + μ u r σ z = E μ ( 1 + μ ) ( 1 − 2 μ ) e + E 1 + μ ∂ w ∂ z τ z r = E 2 ( 1 + μ ) ( ∂ w ∂ r + ∂ u ∂ z ) (8) \begin{cases} \sigma_r=\frac{E\mu}{(1+\mu)(1-2\mu)}e+\frac{E}{1+\mu}\frac{\partial u}{\partial r}\\[1.2ex] \sigma_\theta=\frac{E\mu}{(1+\mu)(1-2\mu)}e+\frac{E}{1+\mu}\frac{u}{r}\\[1.2ex] \sigma_z=\frac{E\mu}{(1+\mu)(1-2\mu)}e+\frac{E}{1+\mu}\frac{\partial w}{\partial z}\\[1.2ex] \tau_{zr}=\frac{E}{2(1+\mu)}(\frac{\partial w}{\partial r}+\frac{\partial u}{\partial z}) \end{cases}\tag8 ⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧σr=(1+μ)(1−2μ)Eμe+1+μE∂r∂uσθ=(1+μ)(1−2μ)Eμe+1+μEruσz=(1+μ)(1−2μ)Eμe+1+μE∂z∂wτzr=2(1+μ)E(∂r∂w+∂z∂u)(8)
另外,
∂ e ∂ r = ∂ 2 e ∂ r 2 + 1 r ∂ u ∂ r − u r 2 + ∂ 2 w ∂ r ∂ z (9) \frac{\partial e}{\partial r}=\frac{\partial^2 e}{\partial r^2}+\frac 1r\frac{\partial u}{\partial r}-\frac u {r^2}+\frac{\partial^2 w}{\partial r\partial z}\tag9 ∂r∂e=∂r2∂2e+r1∂r∂u−r2u+∂r∂z∂2w(9)
对于圆柱坐标系,
∇ 2 u = ∂ 2 u ∂ r 2 + 1 r ∂ u ∂ r + ∂ 2 w ∂ z 2 (10) \nabla^2 u=\frac{\partial^2 u}{\partial r^2}+\frac 1r\frac{\partial u}{\partial r}+\frac{\partial^2 w}{\partial z^2}\tag{10} ∇2u=∂r2∂2u+r1∂r∂u+∂z2∂2w(10)
对于合力 p p p,有:
{ ∂ p ∂ r = E μ 2 ( 1 + μ ) ( 1 1 − 2 μ ∂ e ∂ r + ∇ 2 u − u r 2 ) ∂ p ∂ z = E μ 2 ( 1 + μ ) ( 1 1 − 2 μ ∂ e ∂ z + ∇ 2 w ) (11) \begin{cases} \frac{\partial p}{\partial r}=\frac{E\mu}{2(1+\mu)}\left(\frac1{1-2\mu}\frac{\partial e}{\partial r}+\nabla^2 u-\frac{u}{r^2}\right)\\[1.5ex] \frac{\partial p}{\partial z}=\frac{E\mu}{2(1+\mu)}\left(\frac1{1-2\mu}\frac{\partial e}{\partial z}+\nabla^2 w\right) \end{cases} \tag{11} ⎩⎪⎨⎪⎧∂r∂p=2(1+μ)Eμ(1−2μ1∂r∂e+∇2u−r2u)∂z∂p=2(1+μ)Eμ(1−2μ1∂z∂e+∇2w)(11)