层次分析法

引入

生活中有很多决策问题，需要依据一定的标准选择某一种方案。比如，买衣服一般依据质量、颜色、价格、款式等因素选择。

以一个例子引入：

物品	因素1	因素2	因素3	因素4
A	6000w	10	6.5	25
B	3400w	6	8.1	46
C	5500w	8	7.5	31

如何综合这几个因素，以某种标准，选出A、B、C三者的最优？

显然，直接相加不可取，因为这样因素1掩盖了另外三个，成为决定性因素。因此我们想到，要化为同一数量级，且保证在同一个指标下，差距不变。

可以考虑归一化处理：指标的数组

物品	因素1	因素2	因素3	因素4	评分
A	0.4	0.42	0.29	0.25	1.36
B	0.23	0.25	0.37	0.45	1.30
C	0.37	0.33	0.34	0.30	1.35

实际上，这里的评分栏是简单相加，没有考虑每种因素可能有不同权重，还不够全面，下面加入对加权的考虑。 

物品	因素1（0.4）	因素2（0.3）	因素3（0.2）	因素4（0.1）	评分
A	0.4	0.42	0.29	0.25	0.365
B	0.23	0.25	0.37	0.45	0.293
C	0.37	0.33	0.34	0.30	0.342

这里的权重是随便设置的，不同的权重占比会很大程度上影响排名，实际上这种设置具有很大的主观性，很影响对数据的分析，那么如何科学设置权重？

层次分析法（AHP）

        是对一些较为复杂、较为模糊的问题做出决策的简易方法，它特别适用那些难于完全定量分析的问题。

 原理

        首先把问题条理化、层次化，构造出一个有层次的结构模型。复杂问题被分解为元素的组成部分。这些元素按其属性及其关系形成若干层。上层元素支配下层元素。层次分为三类：

• 最高层：只有一个元素，一般是分析问题的预定目标或理想结果。（例子中选出最优物品）
• 中间层：包含了为实现目标所设计的中间环节，可以由若干层次组成，包括所需的准则、子准则。（例子中各种判断优劣的指标）
• 最底层：包括了为实现目标可供选择的各种措施、决策方案。（A、B、C三个物品）

运用步骤

• 建立递阶层次结构模型
• 构造出各层次中的所有判断矩阵（对指标的重要性进行两两比较，构造判断矩阵，从而科学求出权重；矩阵中元素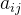的意义是，第i个指标相对于第j个指标的重要程度）

判断矩阵标度

标度	含义
1	两因素具有同样重要性
3	一个比另一个稍微重要
5	一个比另一个明显重要
7	一个比另一个强烈重要
9	一个比另一个极端重要
2，4，6，8	相邻判断的中值

• 一致性检验

        由于构造矩阵时，我们每次都是两两决定重要程度，当变量多了，就容易出现矛盾（因为是人为构造），因此要进行一致性检验。

        正互反矩阵：每个元素大于0且

        一致矩阵：满足的正互反矩阵

        一致性检验步骤：

计算一致性指标CI

查找对应的平均随机一致性指标RI

计算一致性比例CR：

• 求权重后进行评价

求权重步骤

        算数平均法

1.         判断矩阵按照列归一化
2.         归一化的各列相加
3.         相加后得到的向量中每个元素除以n

        几何平均法

1.         判断矩阵按照行相乘得到新的列向量
2.         新向量每个分量开n次方
3.         对该列向量进行归一化

        特征值法

1.         求出矩阵A的最大特征值以及对应的特征向量
2.         对求出的特征向量归一化

Python代码 

import numpy as np


class AHP:
    def __init__(self, array):
        # 记录矩阵相关信息
        self.array = array
        # 记录矩阵大小
        self.n = array.shape[0]
        # 初始化RI值，用于一致性检验
        self.RI_list = [0, 0, 0.52, 0.89, 1.12, 1.26, 1.36, 1.41, 1.46, 1.49, 1.52, 1.54, 1.56, 1.58,
                        1.59]
        # 矩阵的特征值和特征向量
        self.eig_val, self.eig_vector = np.linalg.eig(self.array)
        # 矩阵的最大特征值
        self.max_eig_val = np.max(self.eig_val)
        # 矩阵最大特征值对应的特征向量
        self.max_eig_vector = self.eig_vector[:, np.argmax(self.eig_val)].real
        # 矩阵的一致性指标CI
        self.CI_val = (self.max_eig_val - self.n) / (self.n - 1)
        # 矩阵的一致性比例CR
        self.CR_val = self.CI_val / (self.RI_list[self.n - 1])

    def test_consist(self):
        # 打印矩阵的一致性指标CI和一致性比例CR
        print("判断矩阵的CI值为：" + str(self.CI_val))
        print("判断矩阵的CR值为：" + str(self.CR_val))
        # 进行一致性检验判断
        if self.n == 2:  # 当只有两个子因素的情况
            print("仅包含两个子因素，不存在一致性问题")
        else:
            if self.CR_val < 0.1:  # CR值小于0.1，可以通过一致性检验
                print("判断矩阵的CR值为" + str(self.CR_val) + ",通过一致性检验")
                return True
            else:  # CR值大于0.1, 一致性检验不通过
                print("判断矩阵的CR值为" + str(self.CR_val) + "未通过一致性检验")
                return False

    def cal_weight_by_arithmetic_method(self):
        # 求矩阵的每列的和
        col_sum = np.sum(self.array, axis=0)
        # 将判断矩阵按照列归一化
        array_normed = self.array / col_sum
        # 计算权重向量
        array_weight = np.sum(array_normed, axis=1) / self.n
        # 打印权重向量
        print("算术平均法计算得到的权重向量为：\n", array_weight)
        # 返回权重向量的值
        return array_weight

    def cal_weight__by_geometric_method(self):
        # 求矩阵的每列的积
        col_product = np.product(self.array, axis=0)
        # 将得到的积向量的每个分量进行开n次方
        array_power = np.power(col_product, 1 / self.n)
        # 将列向量归一化
        array_weight = array_power / np.sum(array_power)
        # 打印权重向量
        print("几何平均法计算得到的权重向量为：\n", array_weight)
        # 返回权重向量的值
        return array_weight

    def cal_weight__by_eigenvalue_method(self):
        # 将矩阵最大特征值对应的特征向量进行归一化处理就得到了权重
        array_weight = self.max_eig_vector / np.sum(self.max_eig_vector)
        # 打印权重向量
        print("特征值法计算得到的权重向量为：\n", array_weight)
        # 返回权重向量的值
        return array_weight


if __name__ == "__main__":
    # 给出判断矩阵
    b = np.array([[1, 1 / 3, 1 / 8], [3, 1, 1 / 3], [8, 3, 1]])
    # 一致性检验
    AHP(b).test_consist()
    # 算术平均法求权重
    weight1 = AHP(b).cal_weight_by_arithmetic_method()
    # 几何平均法求权重
    weight2 = AHP(b).cal_weight__by_geometric_method()
    # 特征值法求权重
    weight3 = AHP(b).cal_weight__by_eigenvalue_method()