【第二章】数字信号处理 z变换与离散时间傅里叶变换dtft

开启数字信号处理的理论部分，从z变换入手通过z域到s域的转化，利用信号与系统的知识（傅里叶变换与拉普拉斯变换）开始引入离散时间傅里叶变换，为第三章的离散傅里叶变换/级数埋下伏笔。
对应程佩青《数字信号处理教程》（第五版）第二章内容，推荐结合教材、例题食用，本文仅作思路引入和推进总结使用。

z变换

定义

Z变换定义
$$X(z)=\sum _{n=-\infty }^{\infty }x(n)z^{-n}$$
z反变换定义
$$x(n)=\frac{1}{2\pi j}{\oint }_{c}X(z)z^{n-1}dz$$
z变换存在需满足其表达式（幂级数）收敛，即绝对可和

收敛域

有限长序列

当$n_1\le n\le n_2$，x(n)有值
$X(z)={\sum }_{n=n_1}^{n_2}x(n)z^{-n}$
收敛域至少是有限z平面，$0<|z|<\infty$
当$n_1\ge 0$时，收敛域包括无限远（$\infty$)
当$n_2<0$时，收敛域包含原点(0)
当收敛域包含原点时序列在$-n\le 0$时不能有值，因为$0^{-n}=\frac{1}{0^n}=\infty$

右边序列

当$n\ge n_0$，x(n)有值
$X(z)={\sum }_{n=n_0}^{\infty }x(n)z^{-n}={\sum }_{n=n_0}^{-1}x(n)z^{-n}+{\sum }_{n=0}^{\infty }x(n)z^{-n}$
第一项为有限长序列，收敛域包含有限z平面
故收敛域取决于第二项
$R_{x^{-}}<|z|<\infty$
收敛域在模值最大的极点所在圆之外

因果序列

右边序列的特殊情况，$n_1\ge 0$，收敛域包含无穷远
$R_{x^{-}}<|z|\le \infty$

左边序列

当$n\le n_0$，x(n)有值
$X(z)={\sum }_{n=-\infty }^{n_0}x(n)z^{-n}={\sum }_{n=-\infty }^{-1}x(n)z^{-n}+{\sum }_{n=0}^{n_0}x(n)z^{-n}$
第二项为有限长序列，收敛域取决于第一项
$0<|z|<R_{x^{+}}$
收敛域在模值最小的极点所在圆之内

反因果序列

包含原点

双边序列

分解成一个因果序列和一个非因果序列，收敛域成环
$R_{x^{-}}<|z|<R_{x^{+}}$

常用z变换及收敛域

$\delta (n)\leftrightarrow 10\le |z|\le \infty$
$u(n)\leftrightarrow \frac{z}{z-1}|z|>1$
$u(-n-1)\leftrightarrow -\frac{z}{z-1}|z|<1$

z反变换的求法

留数定理法

把z变换看作洛朗级数$X(z)={\sum }_{n=-\infty }^{\infty }{C}_n{z}^{-n}$
$C_n=x(n)=\frac{1}{2\pi j}{\oint }_{c}X(z)z^{n-1}dz$
可使用留数定理求出洛朗级数的系数从而求出反变换

• 围线内的极点$$x(n)=\sum _{k}Res[X(z)z^{n-1}{]}_{z=z_k}$$
• 围线外的极点$$x(n)=-\sum _{m}Res[X(z)z^{n-1}{]}_{z=z_m}$$
  其中
  $$Res[X(z)z^{n-1}{]}_{z=z_r}=[(z-z_r)X(z)z^n-1{]}_{z=z_r}$$（单阶极点）

围线是在$X(z)$收敛域内的一条闭合曲线
右边序列的极点总包含在围线内
左边序列的极点总是在围线外
若为双边序列，根据n的取值灵活将序列分解成右边序列和左边序列的和，运用不同的公式来简化计算留数

部分分式法

将$X(z)$分解成部分分式的形式（可直接求出反变换的形式）
写成正幂次项展开时，保证分子的最高次幂小于分母，否则需要使用$\frac{X(z)}{z}$的形式进行修正，作为整体分解完后再得到$X(z)$
分子系数的求法：原始$X(z)$形式乘以该项分子对应的分母的式子取值使得分母为零的z值（极点）。如果写成两边同时相乘的形式，右边除该项分子外其他项乘以了使得为零点分母均为零，即证

长除法（幂级数展开法）

使用分式长除法来得到$X(z)$的幂级数表达形式（原来是分式），进而观察幂级数的系数来直接得到x(n)（$X(z)={\sum }_{n}x(n)z^{-n}$）
对于右边序列，写成z的降幂($x(0)+x(1)z^{-1}+...$)
对于左边序列，写成z的升幂($x(0)+x(-1)z^1+...$)
对于有限长序列，可直接观察得到
使用该方法不一定能找到规律进而求出反变换，长除法是除不尽的（原分式本身分子和分母互质），故必须在有限项中观察出规律

z变换的性质

线性性质

$L[x(n)]=X(z),R_{x^{-}}<|z|<R_{x^{+}}$
$L[y(n)]=Y(z),R_{y^{-}}<|z|<R_{y^{+}}$
有$L[ax(n)+by(n)]=aX(z)+bY(z),R_{-}<|z|<R_{+}$
即均匀性（乘法）和叠加性
收敛域一般为两者收敛域的交集
但是最终还是要以结果的表达形式来确定，因为可能会出现零点和极点相互抵消的情况，以最新的极点为准判断收敛域

单边z变换和移位性质

单边z变换

$$L^{+}[x(n)]=L[x(n)u(n)]=X^{+}(z)=\sum _{n=0}^{\infty }x(n)z^{-n}$$
与双边z变换的区别在于仅关心n非负下的z变换，尽管z小于零情况下的信息并没有丢失

移位性质

$L[x(n-m)]=z^{-m}X(z)$
$L^{+}[x(n-m)]=z^{-m}[X^{+}(z)+{\sum }_{i=-m}^{-1}x(i)z^{-i}]$
单边z变换，原序列右移时将原来并未处理的部分序列移入变换范围，需要加上这部分进行z变换的值
$L[x(n+m)]=z^{m}X(z)$
$L_{+}[x(n+m)]=z^m[X^{+}(z)-\sum [i=0{]}^{m-1}x(i)z^{-i}]$
原序列左移后部分序列被移出变换范围需要减去

双边序列移动后收敛域不会变化
单边序列移动后可能会出现“因果序列”、“非因果序列”等范围变化，可能造成$z=0$和$z=\infty$处收敛性的变化

尺度变换

$$L[a^{n}x(n)]=X(\frac{z}{a}),|a|R_{x^{-}}<|z|<|a|R_{x^{+}}$$
对于z反变换的部分因式分解法作用巨大

线性加权性

$$L[nx(n)]=-z\frac{d}{dz}X(z)$$
$$\begin{array}{rl}L[n^{2}x(n)]=& -z\frac{d}{dz}[-z\frac{d}{dz}X(z)]\\ =& z^2\frac{d^2}{d{z}^2}X(z)+z\frac{d}{dz}X(z)\end{array}$$

序列共轭性

$$L[x^{\ast }(n)]=X^{\ast }[z\ast ]$$
通过观察其证明$\begin{array}{rl}L[x^{\ast }(n)]=& \sum _n[x^{\ast }(n)z^{-n}]\\ =& \sum _n[x(n){z^{\ast }}^{-n}{]}^{\ast }\\ =& X^{\ast }[z\ast ]\end{array}$更好的理解含义
对于实序列$x(n)=x^{\ast }(n)$，其极点零点以共轭对形式存在

序列翻褶性

$$L[x(-n)]=X(\frac{1}{z}),\frac{1}{R_{x^{+}}}<|z|<\frac{1}{R_{x^{-}}}$$
引出具有奇偶对称零极点以倒数对形式存在的结论

初值定理

对于因果序列，$li{m}_{z\to \infty }X(z)=x(0)$

终值定理

对于因果序列，且单位圆$|z|=1$上最多可有最高阶为一的极点（一阶极点，保证乘上z-1后在单位圆上收敛），其余极点均在单位圆内，则$$\begin{array}{rl}x(\infty )=& li{m}_{n\to \infty }x(n)\\ =& li{m}_{z\to 1}[(z-1)X(z)]\\ =& Res[X(z){]}_{z=1}\end{array}$$

因果序列的累加性

因果序列$x(n)$
$$L[\sum _{m=0}^{n}x(m)]=\frac{z}{z-1}X(z),|z|>max[R_{x^{-}},1]$$
通过交换求和次序来证明，将m变为0到无穷，n变为m到无穷，这一步通过图2.15（m=n曲线）来理解，该结果也与直觉相符（原式一个x(m)（经累加）就对应多个z，m越大对应的z的个数越少）

时域卷积和定理

$y(n)=x(n)\ast h(n)$
$Y(z)=X(z)H(z)$
收敛域由最终表达式决定

序列相乘（z域复卷积定理）

$y(n)=x(n)h(n)$
$Y(z)=\frac{1}{2\pi j}{\oint }_{c}X(v)H(\frac{z}{v})v^{-1}dv$
收敛域同由表达式决定

帕塞瓦尔定理

由z域复卷积定理可得当$y(n)=x(n)h^{\ast }(n)$，且$Y(z)$在单位圆$|z|=1$上收敛时（$R_{x^{-}}{R}_{h^{-}}<1<R_{x^{+}}{R}_{h^{+}}$），当z=1时
$\begin{array}{rl}Y(z){|}_{z=1}=\sum _{n}x(n)h^{\ast }(n)z^{-n}{|}_{z=1}=& \sum _{n=-\infty }^{\infty }x(n)h^{\ast }(n)\\ =& \frac{1}{2\pi j}{\oint }_{c}X(v)H^{\ast }(\frac{1}{v})v^{-1}dv\end{array}$
当x(n)和h(n)为实序列时，$X(e^{-jw})=X^{\ast }(e^{jw})$
有${\sum }_{n=-\infty }^{\infty }{x}^2(n)=\frac{1}{2\pi }{\int }_{-\pi }^{\pi }|X(e^{jw}){|}^{2}dw$

z变换求解差分方程

对于差分方程${\sum }_{i=0}^N{a}_{i}y(n-i)={\sum }_{m=0}^M{b}_{m}x(n-m)$
由单边z变换的移位性质，两边同时取单边z变换
$$\begin{array}{rl}& \sum _{i=0}^N{a}_i{z}^{-i}[Y^{+}(z)+\sum _{r=-i}^{-1}y(r)z^{-r}]\\ =& \sum _{m=0}^M{b}_m{z}^{-m}[X^{+}(z)+\sum _{l=-m}^{-1}x(l)z^{-l}]\end{array}$$
如要求零输入响应或零状态响应可代入条件求解
对于给出初始条件求总响应，可以直接两边取z变换，但是要考虑移位性质的影响，增加相应的变换项

s平面到z平面映射关系

拉普拉斯变换在s域，z变换在z域
一个隐含关系：抽样信号与连续时间信号的频域关系
${\hat{X}}_a(j\Omega )=\frac{1}{T}{\sum }_{k=-\infty }^{\infty }{X}_a[j(\Omega -k{\Omega }_s)]$
其复频域关系为
${\hat{X}}_a(s)=\frac{1}{T}{\sum }_{k=-\infty }^{\infty }{X}_a(s-jk{\Omega }_s)$

序列z变换与理想抽样信号拉普拉斯变换的关系

连续时间信号$x_a(t)$，对其理想抽样得到的信号为${\hat{x}}_a(t)$
${\hat{x}}_a(t)={\sum }_{n=-\infty }^{\infty }{x}_a(nT)\delta (t-NT)$
其拉普拉斯变换$L[{\hat{x}}_a(t)]={\hat{X}}_a(s)={\sum }_{n=-\infty }^{\infty }{x}_a(nT)e^{-nsT}$
最终表达式是通过交换积分和求和次序得到的
序列由连续时间信号抽样得到，即$x(n)=x_a(nT)$
故$X(z){|}_{z=e^{sT}}=X(e^{sT})={\hat{X}}_a(s)$
当$z=e^{sT}$时（抽样）序列的z变换为其抽样连续时间信号的拉普拉斯变换
运用前面提到的隐含关系得到序列z变换与原始信号关系
$X(z){|}_{z=e^{sT}}={\hat{X}}_a(s)=\frac{1}{T}{\sum }_{k=-\infty }^{\infty }{X}_a(s-jk{\Omega }_s)$
故从s平面到z平面为多值映射关系
z变换与抽样信号s平面为一一对应关系
z变换与原信号s平面为多值映射关系

s域（的实部虚部）与z域（的模值相角）的关系

借助$z=e^{sT}$时序列z变换与理想抽样信号拉普拉斯变换相等的关系来研究z域与s域的关系，此时z域与s域存在相互映射
$z=r{e}^{jw}$
$s=\sigma +j\Omega$
$$\begin{array}{rl}z=e^{sT}=& e^{\sigma T}\cdot e^{j\Omega T}\\ =& r\cdot e^{jw}\end{array}$$
有z域的模值$r=e^{\sigma T}$，z域模值与s域的实部有关
而z域的相角$w=\Omega T$，z域相角与s域的虚部有关
且$e^{jw}$是$w$的周期函数，所以$z=r{e}^{jw}$也是$w$的周期函数，进而与s平面上$\Omega$也有周期关系。故s平面到z平面为多值映射关系，不是一一对应

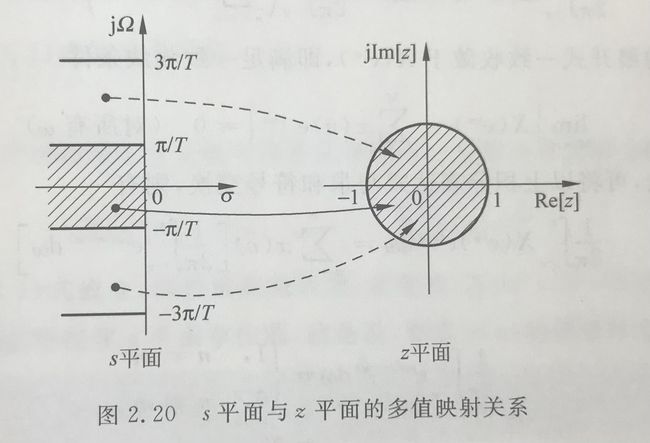
• 当$\sigma =0$，s平面为虚轴时，z域模值为1，对应单位圆$|z|=1$
• 当$\sigma <0$，s域为左半平面时，对应z平面单位圆内
• 当$\delta >0$，s域为右半平面时，对应z平面单位圆外

序列z变换与理想抽样信号傅立叶变换的关系

理想抽样信号${\hat{x}}_a(t)$的傅立叶变换${\hat{X}}_a(j\Omega )$ 与拉普拉斯变换${\hat{X}}_a(s)$的关系为${\hat{X}}_a(j\Omega )={\hat{X}}_a(s){|}_{s=j\Omega }$
当$s=j\Omega$时，对应的实部$\sigma =0$，对应z域的单位圆
（$z=e^{sT}=(e^{\sigma T}{|}_{\sigma =0})\cdot e^{j\Omega T}=1\cdot e^{j\omega }$）
再利用${\hat{X}}_a(s)=X(z){|}_{z=e^{sT}}=X(e^{sT})$
有${\hat{X}}_a(j\Omega )=X(z){|}_{z=e^{sT}{|}_{s=j\Omega }}=X(z){|}_{z=e^{j\Omega T}}=X(z){|}_{z=e^{jw}}=X(e^{jw})$
序列在单位圆上的z变换等于理想抽样信号的傅立叶变换
（在前一步得到了z平面与s平面的关系，这里的条件在单位圆上就对s平面的范围进行了限制（虚轴上））
同样的得到与原始信号的关系
$X(z){|}_{z=e^{j\Omega T}}=X(e^{j\Omega T})=X(e^{j\omega })={\hat{X}}_a(j\Omega )=\frac{1}{T}{\sum }_{k=-\infty }^{\infty }{X}_a(j\frac{\omega -2\pi k}{T})$

（接前面继续研究z域与s域的关系）

• 当$\Omega =0$，s域为实轴时，z平面为幅角为0的射线
  因此若$\sigma$（模值）和$\Omega$（相角）都确定，在s平面上的位置（一个点已知），（“圆和射线取交集”），就得到了z平面上的一个点

DTFT-离散时间傅立叶变换

DTFT表达式及周期性

在[[#序列z变换与理想抽样信号傅立叶变换的关系]]中得到了理想抽样信号${\hat{x}}_a(t)={\sum }_{n=-\infty }^{\infty }{x}_a(nT)\delta (t-nT)$的傅立叶变换形式，对应的序列为$x(n)=x_a(t){|}_{t=nT}=x_a(nT)$，傅立叶变换${\hat{X}}_a(j\Omega )=X(e^{jw})$为序列$x(n)$的离散时间傅立叶变换
$DTFT[x(n)]=X(e^{jw})=X(z){|}_{z=e^{jw}}={\sum }_{n=-\infty }^{\infty }x(n)e^{-jwn}$
其反变换是在一个周期上进行积分得到的，积分区间为$[-\pi ,\pi ]$
$IDTFT[X(e^{jw})]=x(n)=\frac{1}{2\pi }{\int }_{-\pi }^{\pi }X(e^{jw})e^{jwn}dw$
序列的离散时间傅立叶变换得到的$X(e^{jw})$为$x(n)$的频谱密度（频谱），包含幅度谱$|X(e^{jw})|$和相位谱$arg[X(e^{jw})]$ ，可以表示为$X(e^{jw})=|X(e^{jw})|e^{jarg[X(e^{jw})]}$ ，以$2\pi$为周期。而周期函数可以用傅立叶级数展开，可以把其定义式${\sum }_{n=-\infty }^{\infty }x(n)e^{-jwn}$看作是其傅立叶级数，系数为$x(n)$

DTFT收敛性及存在条件

一致收敛（绝对可和）

序列的傅立叶变换为序列在单位圆上的z变换，由z变换的收敛域可得$X(z)$的收敛域必须包含单位圆，在$|z|=1$处收敛,z变换收敛的条件是绝对可和，即$|X(e^{jw})|<\infty$
而$\begin{array}{rl}|X(e^{jw})|=& |\sum _{n=-\infty }^{\infty }x(n)e^{-jwn}|\le \sum _{n=-\infty }^{\infty }|x(n)||e^{-jwn}|\\ \le & \sum _{n=-\infty }^{\infty }|x(n)|\\ <& \infty \end{array}$
故有${\sum }_{n=-\infty }^{\infty }|x(n)|<\infty$，序列绝对可和为DTFT存在充分条件

均方收敛 （平方可和）

DTFT存在的另一充分条件
由一致收敛条件可得$[{\sum }_{n=-\infty }^{\infty }|x(n)|{]}^2<\infty$
而${\sum }_{n=-\infty }^{\infty }{|x(n)|}^2\le {[{\sum }_{n=-\infty }^{\infty }|x(n)|]}^2<\infty$
一致收敛可以得到均方收敛，反之不一定

非非周期序列的DTFT

周期性序列、单位阶跃序列引入冲激函数也可得到DTFT

DTFT的性质

可由z变换的性质得来，将$z$换成$e^{jw}$

序列的分解与对称性质

序列的分解及其分解式的表示

对于频谱也同样适用

虚实分解

一个序列可以表示成实部和虚部乘j之和
$$x(n)=Re[x(n)]+jIm[x(n)]$$
$$x^{\ast }(n)=Re[x(n)]-jIm[x(n)]$$
故$Re[x(n)]=\frac{1}{2}[x(n)+x^{\ast }(n)]$
$jIm[x(n)]=\frac{1}{2}[x(n)-x^{\ast }(n)]$
对于实序列，$x(n)=x^{\ast }(n)$
代入$Re[x(n)]$和$Im[x(n)]$只有实部存在！

对称分解

表示成共轭对称序列和反共轭对称序列之和
$$x(n)=x_e(n)+x_o(n)$$
共轭对称序列满足$x_e(n)=x_e^{\ast }(-n)$
对其进行虚实分解$x_e(n)=Re[x_e(n)]+jIm[x_e(n)]$
则$x_e^{\ast }(-n)=Re[x_e(-n)]-jIm[x_e(-n)]$
那么有
$Re[x_e(n)]=Re[x_e(-n)]$，共轭对称序列实部为偶函数
$Im[x_e(n)]=-Im[x_e(-n)]$，共轭对称序列虚部为奇函数

共轭反对称序列满足$x_o(n)=-x_o^{\ast }(-n)$
$Re[x_o(n)]=-Re[x_o(-n)]$，共轭反对称序列实部为奇函数
$Im[x_o(n)]=Im[x_o(-n)]$，共轭反对称序列虚部为偶函数
因此有$$\begin{array}{rl}{x}^{\ast }(-n)=& x_e^{\ast }(-n)+x_o^{\ast }(-n)\\ =& x_e(n)-x_o(n)\end{array}$$
故$x_e(n)=\frac{1}{2}[x(n)+x^{\ast }(-n)]$
$x_o(n)=\frac{1}{2}[x(n)-x^{\ast }(-n)]$
对于实序列，可将所有共轭号去掉，成为奇对称序列和偶对称序列分解
若序列为因果序列，可从$x_e(n)$或$x_o(n)$恢复出$x(n)$，通过下面的对偶关系又可以知道可以从$X(e^{jw})$的实部或虚部得到（只用到实部或虚部中的一个，故说频谱含冗余信息）
$x(n)=\{\begin{array}{ll}2x_e(n)& n>0\\ x_e(n)& n=0\\ 0& n<0\end{array}$
或者
$x(n)=\{\begin{array}{ll}2x_o(n)& n>0\\ x(0)& n=0\\ 0& n<0\end{array}$

时域与频域的对偶关系

通过DTFT作为桥梁可以在时域和频域上转化这两种分解方式
用到的重要性质：$DTFT[x^{\ast }(n)]=X^{\ast }(e^{-jw})$
($DTFT[x(n)]=X(e^{jw})$)，通过这一步大大加深理解了[[#序列共轭性]]的定义和应用
$x(n)=Re[x(n)]+jIm[x(n)]$
$X(e^{jw})=X_e(e^{jw})+X_o(e^{jw})$
证明：将时域形式的分解方式的两个基$Re[x(n)]$和$jIm[x(n)]$用$x(n)$及$x^{\ast }(n)$表示，再对两边进行DTFT，通过找到对应的项表示成下面的形式。重要的是熟记对序列进行分解的分解项用原序列（及其共轭或反共轭）的表示方法。
$x(n)=x_e(n)+x_o(n)$
$X(e^{jw})=Re[X(e^{jw})]+jIm[X(e^{jw})]$

若$x(n)$为实序列，时域只有$Re[x(n)]$，则频域只有$X_e(e^{jw})$，那么$X(e^{jw})$为共轭对称序列
有$X(e^{jw})=X^{\ast }(e^{-jw})$，实部（模值）偶对称，虚部（相角）奇对称
$|X(e^{jw})|=|X(e^{-jw})|$
$arg[X(e^{jw})]=-arg[X(e^{-jw})]$

周期序列的DTFT

复指数序列

$$e^{j{w}_{0}n}⟷\sum _{i=-\infty }^{\infty }2\pi \delta (w-w_0-2\pi i)$$
通过傅立叶反变换公式代入成立得证

常数序列

复指数序列$w_0=1$的特殊情况
$$1⟷\sum _{i=-\infty }^{\infty }2\pi \delta (w-2\pi i)$$
也可以用$x(n)={\sum }_{i=-\infty }^{\infty }\delta (n-i)$来表示

单位抽样序列

$x(n)={\sum }_{i=-\infty }^{\infty }\delta (n-iN)$，周期为$N$
$$\sum _{i=-\infty }^{\infty }\delta (n-iN)⟷\frac{2\pi }{N}\sum _{k=-\infty }^{\infty }\delta (w-\frac{2\pi }{N}k)$$
证明：由于${\sum }_{i=-\infty }^{\infty }\delta (n-i)⟷{\sum }_{i=-\infty }^{\infty }2\pi \delta (w-2\pi i)$
也可以表示成${\sum }_{n=-\infty }^{\infty }{e}^{-jwn}={\sum }_{i=-\infty }^{\infty }2\pi \delta (w-2\pi i)$
（左边为1的DFFT定义式）
注意左边变量为n，如果换成i为
${\sum }_{i=-\infty }^{\infty }{e}^{-jwi}={\sum }_{i=-\infty }^{\infty }2\pi \delta (w-2\pi i)$
$\begin{array}{rl}DTFT[\sum _{i=-\infty }^{\infty }\delta (n-iN)]=& \sum _{n=-\infty }^{\infty }[\sum _{i=-\infty }^{\infty }\delta (n-iN)]e^{-jwn}\\ =& \sum _{i=-\infty }^{\infty }[\sum _{n=-\infty }^{\infty }\delta (n-iN)e^{-jwn}]\\ =& \sum _{i=-\infty }^{\infty }{e}^{-jwNi}\end{array}$
这个式子的变量为i，因此套用上一条式子有
${\sum }_{i=-\infty }^{\infty }{e}^{-j(Nw)i}={\sum }_{i=-\infty }^{\infty }2\pi \delta (Nw-2\pi i)$
冲激函数满足$\delta (at)=\frac{1}{|a|}\delta (t)$
因此右边写作$\frac{2\pi }{N}{\sum }_{i=-\infty }^{\infty }\delta (w-\frac{2\pi }{N}i)$
换成k即证

周期性序列与离散傅里叶级数

周期为N的序列$\begin{array}{rl}\tilde{x}(n)=& \sum _{i=-\infty }^{\infty }x(n-iN)\\ =& x(n)\ast \sum _{i=-\infty }^{\infty }\delta (n-iN)\end{array}$
为有限长序列$x(n)$与周期为N的单位抽样序列的卷积
$$\sum _{i=-\infty }^{\infty }x(n-iN)⟷\frac{2\pi }{N}\sum _{k=-\infty }^{\infty }\tilde{X}(k)\delta (w-\frac{2\pi }{N}k)$$
再利用DTFT的时域卷积性质
$\begin{array}{rl}\tilde{X}(e^{jw})=& DTFT[x(n)]\cdot DTFT[\sum _{i=-\infty }^{\infty }\delta (n-iN)]\\ =& X(e^{jw})\cdot \frac{2\pi }{N}\sum _{k=-\infty }^{\infty }\delta (w-\frac{2\pi }{N}k)\\ =& \frac{2\pi }{N}\sum _{k=-\infty }^{\infty }X(e^{j\frac{2\pi }{N}k})\delta (w-\frac{2\pi }{N}k)\\ =& \frac{2\pi }{N}\sum _{k=-\infty }^{\infty }\tilde{X}(k)\delta (w-\frac{2\pi }{N}k)\end{array}$
其在频域上是离散的，为离散傅里叶级数
其中$\tilde{X}(k)$为离散傅里叶级数的系数，等于有限长序列$x(n)$DTFT在某点$w=\frac{2\pi k}{N}$处的抽样值
$\tilde{X}(k)=X(e^{jw}){|}_{w=\frac{2\pi }{N}k}={\sum }_{n=0}^{N-1}{e}^{-j\frac{2\pi }{N}nk}$
离散傅里叶级数逆变换$\tilde{x}(n)=\frac{1}{N}{\sum }_{k=0}^{N-1}\tilde{X}(k)e^{j\frac{2\pi }{N}kn}$

离散LSI系统的频域表征

LSI系统的表示方法

• 时域
  • 单位冲激响应$h(n)$
  • 常系数线性差分方程
• 频域
  • 系统函数$H(z)$
  • 频率响应$H(e^{jw})$（当系统函数在z平面单位圆收敛）

LSI系统的因果、稳定条件

因果性

• 时域
  $h(n)=0,n<0$
• z域
  $R_{h^{-}}<|z|\le \infty$，$H(z)$收敛域在某圆外，包含无穷远

稳定性

• 时域
  ${\sum }_{n=-\infty }^{\infty }|h(n)|<\infty$
• z域
  $H(z)$收敛域包含单位圆，即有${\sum }_{n=-\infty }^{\infty }|h(n)z^{-n}{|}_{|z|=1}={\sum }_{n=0}^{\infty }|h(n)|<\infty$
  若收敛域$|z|>1$，则缩小了累加值，不满足

因果稳定性

z域条件（充分必要）：

• 从单位圆到无穷远z平面收敛，$1\le |z|\le \infty$
• $H(z)$所有极点在单位圆内
  上面主要考虑到了必要条件，也就是最小的可能从系统因果稳定推到z平面收敛域的范围
  仅考虑充分性，$R_{h^{-}}<1\le |z|<\infty$

LSI系统频率响应

LSI系统单位冲激响应$h(n)$已知，输入特征函数$x(n)=e^{jwn}$（复指数序列/正弦），输出为$\begin{array}{rl}y(n)=& x(n)\ast h(n)=\sum _{m=-\infty }^{\infty }h(m)x(n-m)\\ =& e^{jwn}\sum _{m=-\infty }^{\infty }h(m)e^{-jwm}\\ =& e^{jwn}H(e^{jw})\end{array}$

$H(e^{jw})$称作LSI系统的特征值，为系统的频率响应
性质：输入为复指数序列/正弦序列，经过LSI系统，输出的正弦序列频率相同，但是幅度被频率响应幅度$|H(e^{jw})|$加权（不是常数与具体的$w$有关），相位为输入相位和系统响应相位之和
$|e^{jwn}|=1$，$|e^{jwn}H(e^{jw})|=H(e^{jw})$
$arg[e^{jwn}H(e^{jw})]=arg[e^{jwn}]+arg[H(e^{jw})]$,
对于具体的某频率$w_o$的分量，经过LSI系统，频率乘$|H(e^{j{w}_0})|$，相位加$arg[H(e^{j{w}_0})]$

频率响应的几何确定法

系统函数$H(z)$可以表示成$\begin{array}{r}H(z)=K{z}^{N-M}\frac{{\prod }_{m=1}^{M}z-c_m}{{\prod }_{k=1}^{N}z-d_k}\end{array}$
$z^{N-M}$项对应在z平面原点处的零点或极点，当N>M，为(N-M)阶零点；当N

应用：根据零极点来判断滤波器形式（低通、高通、带通、带阻）

已经给出系统零极点，系统在单位圆上收敛，由使用零极点形式表示的系统函数来确定系统的幅频响应$|H(e^{jw})|$，则可根据z域上单位圆对应的$w$的零矢（零点指向单位圆上对应$e^{jw}$点的矢量）和极矢（极点指向单位圆上对应$e^{jw}$点的矢量）大致画出$w\in [0,2\pi ]$上的$H(e^{jw})$，判断出滤波器的类型。