算法设计与分析-Divide and conquer 「国科大」卜东波老师
1.Question Number 1
You are interested in analyzing some hard-to-obtain data from two separate databases. Each database contains n numerical values, so there are 2n values total and you may assume that no two values are the same. You’d like to determine the median of this set of 2n values, which we will define here to be the nth smallest value. However, the only way you can access these values is through queries to the databases. In a single query, you can specify a value k to one of the two databases, and the chosen database will return the kth smallest value that it contains. Since queries are expensive, you would like to compute the median using as few queries as possible. Give an algorithm that finds the median value using at most O(logn) queries.
1.1 问题重述
这个问题涉及从两个不同的数据库中分析一些难以获取的数据。每个数据库包含n个数值,因此总共有2n个数值,并且假设这些值各不相同。目标是确定这2n个值的中位数,我们在这里将其定义为第n小的值。然而,你获取这些值的唯一方式是通过对数据库进行查询。在一次查询中,你可以向其中一个数据库指定一个值k,所选数据库将返回它所包含的第k小的值。由于查询成本高昂,你希望使用尽可能少的查询次数来计算中位数。给出一个算法,使用最多O(logn)次查询来找到中位数。
这个问题可以使用一种类似于二分搜索的算法来解决。算法的基本思想是在两个数据库之间进行二分搜索,以找到整个2n个数中的第n小的数,即中位数。
这个问题的核心是使用最少的查询次数(O(logn))来找到两个数据库中总共2n个数值的中位数。为了解决这个问题,我们可以采用一种类似于二分搜索的策略。具体算法思路如下:
-
初始化搜索范围:由于每个数据库包含n个数值,我们可以为每个数据库设置初始搜索范围。这个范围从1到n,其中1表示最小值,n表示最大值。
-
二分搜索过程:
- 在每次迭代中,我们分别从两个数据库中找到当前搜索范围的中点位置对应的数值。设这两个中点位置为
mid1和mid2,分别位于两个数据库中。 - 然后,我们分别对两个数据库执行查询,获得这两个位置的数值,设为
val1和val2。 - 接下来,比较这两个数值。根据比较的结果,我们调整搜索范围:
- 如果
val1大于val2,则我们知道中位数不可能在第一个数据库的mid1之后,也不可能在第二个数据库的mid2之前。因此,我们将第一个数据库的搜索范围调整为[left1, mid1-1],将第二个数据库的搜索范围调整为[mid2+1, right2]。 - 如果
val1小于或等于val2,则调整方式相反。
- 如果
- 在每次迭代中,我们分别从两个数据库中找到当前搜索范围的中点位置对应的数值。设这两个中点位置为
-
重复过程:重复上述过程,直到搜索范围缩小到只有一个数值。这个数值即为所求的中位数。
-
最终结果:在搜索范围缩小到一个数值时,从两个数据库中选出较小的那个数值,它就是整个2n个数值的中位数。
1.2算法描述(自然语言)
-
初始化:设置两个数据库的搜索范围,分别为左边界
left1 = 1和left2 = 1,右边界right1 = n和right2 = n。 -
二分搜索:当
left1 <= right1和left2 <= right2时,重复以下步骤:- 计算每个数据库当前搜索范围的中点,即
mid1 = (left1 + right1) / 2和mid2 = (left2 + right2) / 2。 - 向两个数据库分别查询第
mid1小和第mid2小的值,分别记为val1和val2。 - 比较
val1和val2,并基于比较结果调整搜索范围:- 如果
val1 > val2,则调整第一个数据库的右边界为mid1 - 1,第二个数据库的左边界为mid2 + 1。 - 如果
val1 < val2,则调整第一个数据库的左边界为mid1 + 1,第二个数据库的右边界为mid2 - 1。
- 如果
- 计算每个数据库当前搜索范围的中点,即
-
确定中位数:当搜索范围缩小到只剩一个值时,比较两个数据库中的这两个值,较小的那个即为中位数。
1.3伪代码
function findMedian(database1, database2, n):
left1, right1 = 1, n
left2, right2 = 1, n
while left1 <= right1 and left2 <= right2:
mid1 = (left1 + right1) / 2
mid2 = (left2 + right2) / 2
val1 = query(database1, mid1)
val2 = query(database2, mid2)
if val1 > val2:
right1 = mid1 - 1
left2 = mid2 + 1
else:
left1 = mid1 + 1
right2 = mid2 - 1
return min(query(database1, left1), query(database2, left2))
1.4算法正确性证明
这个算法基于二分搜索的原理。每次比较两个数据库中的中点值,通过比较结果缩小搜索范围。由于数据集中没有重复的值,我们可以确保在每一步比较中,至少有一半的数据被排除在中位数的候选之外。因此,算法最终将准确地定位到第n小的值,即2n个值的中位数。
1.5复杂度分析
- 时间复杂度:每次查询都将搜索范围减半,所以总的查询次数为O(logn)。
- 空间复杂度:由于算法仅使用固定数量的变量存储索引和值,因此空间复杂度为O(1)。
======================================================================
2.Question Number 2
Given any 10 points, p1, p2, …, p10, on a two-dimensional Euclidean plane, please write an algorithm to find the distance between the closest pair of points.
(a) Using a brute-force algorithm to solve this problem, analyze the time complexity of your implemented brute-force algorithm and explain why the algorithm’s time complexity is O(n2), where n is the number of points.
(b) Propose an improved algorithm to solve this problem with a time complexity better than the brute-force algorithm. Describe the algorithm’s idea and analyze its time complexity.
2.1 问题重述
给定二维欧几里得平面上的任意10个点,p1、p2、…、p10,请编写一个算法来找到这些点中最近的一对点之间的距离。
(a) 使用暴力算法解决这个问题,分析你实现的暴力算法的时间复杂度,并解释为什么该算法的时间复杂度是O(n^2),其中n是点的数量。
(b) 提出一种改进的算法来解决这个问题,该算法的时间复杂度优于暴力算法。描述该算法的思想,并分析其时间复杂度。
2.2算法描述
(a) 暴力算法
暴力算法遍历每一对点,并计算它们之间的距离,记录最小距离。
自然语言描述:
- 初始化最小距离为无穷大。
- 对于每一对点 (pi, pj),计算它们之间的欧几里得距离。
- 如果这个距离小于当前记录的最小距离,则更新最小距离。
- 最终返回最小距离。
伪代码:
function bruteForceClosestPair(points):
min_distance = INFINITY # 初始化最小距离为无限大
for i from 0 to length(points) - 1: # 对于每个点pi
for j from i+1 to length(points): # 与pi之后的每个点pj进行比较
distance = calculateDistance(points[i], points[j]) # 计算点pi和pj之间的距离
if distance < min_distance: # 如果找到了更小的距离
min_distance = distance # 更新最小距离
return min_distance # 返回找到的最小距离
时间复杂度分析:
- 时间复杂度为 O(n^2),其中 n 是点的数量。这是因为需要对每一对点进行比较,总共有 n(n-1)/2 对比较。
(b) 分治算法
分治算法通过将点集分为两个子集,分别计算子集中最近点对的距离,然后在边界上查找可能更近的点对。
自然语言描述:
- 按x坐标对点进行排序。
- 将点集分为两个大致相等大小的子集。
- 递归地在两个子集中找到最近点对的距离。
- 在两个子集的边界上查找可能存在的更近的点对。
- 返回最小的距离。
伪代码:
function divideAndConquerClosestPair(points):
sort points by x-coordinate # 按照x坐标对点进行排序
return closestPairRec(points) # 调用递归函数来找最近点对
function closestPairRec(points):
if length(points) <= 3: # 如果点的数量小于等于3
return bruteForceClosestPair(points) # 使用暴力方法计算最近点对
mid = length(points) / 2 # 找到中点
left = points[0..mid] # 左半部分的点
right = points[mid+1..end] # 右半部分的点
d_left = closestPairRec(left) # 递归计算左半部分的最近点对距离
d_right = closestPairRec(right) # 递归计算右半部分的最近点对距离
d = min(d_left, d_right) # 找到左右两部分中的最小距离
return min(d, closestPairInStrip(points, d)) # 比较分割线附近的点对,返回最小距离
function closestPairInStrip(points, d):
# 在两个分割部分之间的条带内查找可能存在的更近的点对
# 这部分通常需要按y坐标排序并进行高效的比较
...
时间复杂度分析:
- 时间复杂度为 O(n log n)。这是因为点集被递归地分成两半,每一层的复杂度为 O(n),总共有 O(log n) 层。
2.3算法正确性证明
(a) 暴力算法
暴力算法通过对每一对点进行比较,确保没有遗漏任何可能的点对,因此可以保证找到最近的点对。
(b) 分治算法
分治算法在两个子集中找到的最近点对是局部最优的。在边界上的查找确保了如果存在跨越两个子集的更近的点对,也能被发现。因此,算法能够保证全局最优解。
2.4复杂度分析
(a) 暴力算法
- 时间复杂度:O(n^2)。对于n个点,有n(n-1)/2种点对组合需要计算。
(b) 分治算法
- 时间复杂度:O(n log n)。点集被分成两半,每半的处理时间为T(n/2),加上合并时的O(n)操作,总共有T(n) = 2T(n/2) + O(n),符合O(n log n)的复杂度。
2.5代码实现
import math
def calculate_distance(p1, p2):
"""计算两点之间的欧氏距离"""
return math.sqrt((p1[0] - p2[0]) ** 2 + (p1[1] - p2[1]) ** 2)
def brute_force_closest_pair(points):
"""暴力方法找到最近点对的距离"""
min_distance = float('inf')
n = len(points)
for i in range(n):
for j in range(i + 1, n):
distance = calculate_distance(points[i], points[j])
if distance < min_distance:
min_distance = distance
return min_distance
def closest_pair_in_strip(points, d):
"""在条带中找到可能更近的点对"""
min_distance = d
points.sort(key=lambda point: point[1]) # 按y坐标排序
n = len(points)
for i in range(n):
for j in range(i + 1, n):
if points[j][1] - points[i][1] < min_distance:
distance = calculate_distance(points[i], points[j])
min_distance = min(min_distance, distance)
else:
break
return min_distance
def divide_and_conquer_closest_pair(points):
"""分治方法找到最近点对的距离"""
def closest_pair_rec(points_sorted):
"""递归地找到最近点对"""
if len(points_sorted) <= 3:
return brute_force_closest_pair(points_sorted)
mid = len(points_sorted) // 2
left_points = points_sorted[:mid]
right_points = points_sorted[mid:]
d_left = closest_pair_rec(left_points)
d_right = closest_pair_rec(right_points)
d = min(d_left, d_right)
# 查找跨越左右部分的最近点对
strip = [point for point in points_sorted if abs(point[0] - points_sorted[mid][0]) < d]
d_strip = closest_pair_in_strip(strip, d)
return min(d, d_strip)
points_sorted = sorted(points, key=lambda point: point[0])
return closest_pair_rec(points_sorted)
# 示例
points = [(1, 2), (3, 4), (5, 6), (7, 8), (9, 10), (2, 1), (4, 3), (6, 5), (8, 7), (10, 9)]
result = divide_and_conquer_closest_pair(points)
result
1.4142135623730951
calculate_distance(p1, p2): 计算两点之间的欧氏距离。
brute_force_closest_pair(points): 暴力方法,遍历每一对点并计算它们之间的距离,记录并返回最小距离。
closest_pair_in_strip(points, d): 在一条宽度为d的条带中找到最近的点对。首先按照y坐标对点进行排序,然后遍历点对比较它们的距离。
divide_and_conquer_closest_pair(points): 分治方法的主函数。首先按x坐标对点进行排序,然后递归地在左右两个子集中找到最近点对的距离。
closest_pair_rec(points_sorted): 递归函数,用于分治算法中处理子问题。当点的数量小于或等于3时,使用暴力方法计算最近点对的距离。否则,将点集分为左右两部分,递归地在每部分中找到最近点对的距离,然后在跨越两部分的条带中找可能存在的更近的点对。
======================================================================
3.Question Number 3
Given an integer n, where 100 < n < 10000, please design an efficient algorithm to calculate the last digits of 3 n 3^n 3n, with a time complexity not exceeding O(n).
(a) Implement a naive calculation method to compute 3n and analyze the time complexity of the naive calculation method.
(b) Propose an improved algorithm to calculate 3n with a time complexity not exceeding O(n). Describe the algorithm’s concept and analyze its time complexity.
3.1问题重述
给定一个整数n,其中100 < n < 10000,请设计一个高效的算法来计算 3 n 3^n 3n 的最后5位数字,其时间复杂度不超过O(n)。
(a) 实现一个朴素的计算方法来计算 3 n 3^n 3n,并分析这种朴素计算方法的时间复杂度。
(b) 提出一种改进的算法来计算 3 n 3^n 3n,其时间复杂度不超过O(n)。描述该算法的概念,并分析其时间复杂度。
3.2算法描述
(a) 朴素计算方法
这个方法直接计算 3 n 3^n 3n,然后提取其最后五位数字。
自然语言描述:
- 从1开始,连乘3,共乘n次。
- 每次乘法后取模100000,以保留最后五位。
- 最终结果是 3 n 3^n 3n 的最后五位数字。
伪代码:
function naive_power_3(n):
result = 1
for i in range(n):
result = (result * 3) % 100000
return result
时间复杂度分析:
- 时间复杂度为 O(n),因为有一个直到n的循环。
(b) 改进的算法
这个算法采用迭代的方式来加速幂的计算。
自然语言描述:
- 使用快速幂算法:将幂分解为若干个2的幂次的乘积。
- 递归地计算 3 n / 2 3^{n/2} 3n/2,然后相乘。
- 如果n是奇数,再乘以3。
- 在每一步都取模100000,以避免大数问题。
伪代码:
function fast_power_3(n):
if n == 0:
return 1
half = fast_power_3(n // 2)
result = (half * half) % 100000
if n % 2 == 1:
result = (result * 3) % 100000
return result
时间复杂度分析:
- 时间复杂度为 O(log n),因为每次递归都将n减半。
3.3算法正确性证明
(a) 朴素方法
这个方法直接计算 3 n 3^n 3n,每次乘法后立即取模,以保持数字在可控范围内。因此,它能准确计算出 3 n 3^n 3n 的最后五位。
(b) 改进的算法
快速幂算法基于分治法。它将 3 n 3^n 3n 分解为较小的部分递归计算,这些部分的结果再组合起来。由于每一步都进行取模操作,因此可以保证结果的准确性。
3.4复杂度分析
(a) 朴素方法
- 时间复杂度:O(n),因为有一个循环运行n次。
(b) 改进的算法
- 时间复杂度:O(log n),因为每次递归都将问题规模减半。
3.5python实现
def naive_power_3(n):
"""朴素方法计算3的n次幂的最后五位数字"""
result = 1
for _ in range(n):
result = (result * 3) % 100000
return result
def fast_power_3(n):
"""快速方法计算3的n次幂的最后五位数字"""
if n == 0:
return 1
half = fast_power_3(n // 2)
result = (half * half) % 100000
if n % 2 == 1:
result = (result * 3) % 100000
return result
# 示例
n = 157
naive_result = naive_power_3(n)
fast_result = fast_power_3(n)
naive_result, fast_result
(20563, 20563)
3.6写一个函数记录代码执行多少行
import inspect
import sys
def count_executed_lines(func, *args):
"""统计函数执行时的行数"""
# 获取函数源代码的行号
source_lines = inspect.getsourcelines(func)[0]
first_line_no = inspect.getsourcelines(func)[1]
# 记录每行代码是否执行过
executed = [0] * len(source_lines)
# 追踪函数执行时的行号
def tracer(frame, event, arg):
if event == 'line':
lineno = frame.f_lineno
index = lineno - first_line_no
if 0 <= index < len(executed):
executed[index] += 1
return tracer
# 设置追踪器
sys.settrace(tracer)
# 执行函数
func(*args)
# 停止追踪
sys.settrace(None)
# 计算执行过的行数
return sum(executed)
# 统计朴素方法和快速方法执行的行数
naive_executed_lines = count_executed_lines(naive_power_3, n)
fast_executed_lines = count_executed_lines(fast_power_3, n)
naive_executed_lines, fast_executed_lines
(317, 47)
在计算 3 157 3^{157} 3157 时:
- 朴素方法 (
naive_power_3) 实际执行了 317 行代码。 - 快速方法 (
fast_power_3) 实际执行了 47 行代码。
尽管快速方法在代码层面上看起来更复杂,但在实际执行时它执行的代码行数远少于朴素方法,
======================================================================
4 Question Number 4
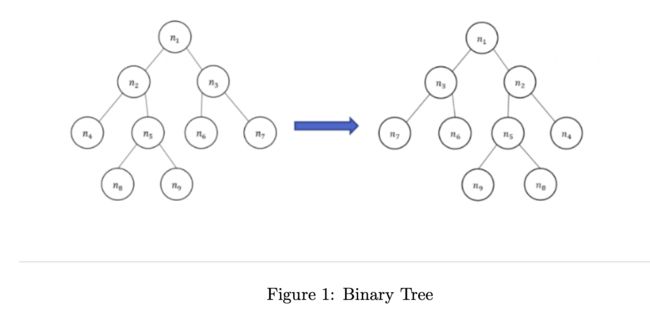
Given a binary tree T, please give an O(n) algorithm to invert binary tree. For example below,inverting the left binary tree, we get the right binary tree.
4.1问题重述
给定一个二叉树T,请给出一个时间复杂度为O(n)的算法来翻转这个二叉树。例如下图所示,翻转左边的二叉树后,我们得到了右边的二叉树。
这个问题要求我们给出一个反转二叉树的算法。反转二叉树,即将所有节点的左子树和右子树交换。
4.2算法思路
-
递归法:
- 如果当前遍历到的节点为空,返回空,不进行交换。
- 交换当前节点的左子树和右子树。
- 递归地对当前节点的左子节点(原来的右子树)进行反转。
- 递归地对当前节点的右子节点(原来的左子树)进行反转。
- 返回当前节点(现在已经被反转)。
-
迭代法:
- 使用一个队列来进行层序遍历。
- 在遍历过程中,交换每个节点的左右子节点。
- 继续遍历直到队列为空。
4.3 伪代码
function invertBinaryTree(root):
if root is None:
return None
# 交换左右子树
root.left, root.right = root.right, root.left
# 递归反转子树
invertBinaryTree(root.left)
invertBinaryTree(root.right)
return root
4.4 算法正确性证明
该算法简单地遍历了每个节点一次,并且在遍历的过程中交换了每个节点的左右子树。由于每个节点都被遍历且只被遍历一次,所以每个节点的左右子树都会被交换,从而实现了整个树的反转。
4.5 复杂度分析
无论是递归方法还是迭代方法,我们都需要访问二叉树中的每个节点一次。
- 时间复杂度:O(n),其中n是树中的节点数量。
- 空间复杂度:对于递归方法,最坏情况下是O(n)(不平衡的树),平均情况下是O(log n)(平衡的树);对于迭代方法,空间复杂度是O(n),因为需要额外的队列来存储节点。
4.6 举例
# 1
# / \
# 2 3
# / \ / \
# 4 5 6 7
class TreeNode:
"""Definition for a binary tree node."""
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
def invert_tree(node):
"""Inverts a binary tree."""
if node is None:
return None
# Swap the left and right subtree
node.left, node.right = node.right, node.left
# Recursively invert the left and right subtree
invert_tree(node.left)
invert_tree(node.right)
return node
# Helper function to print the tree in-order (for verification)
def print_tree(node):
if node is not None:
print_tree(node.left)
print(node.val, end=' ')
print_tree(node.right)
# Constructing the binary tree shown in the example
# 1
# / \
# 2 3
# / \ / \
# 4 5 6 7
root = TreeNode(1)
root.left = TreeNode(2)
root.right = TreeNode(3)
root.left.left = TreeNode(4)
root.left.right = TreeNode(5)
root.right.left = TreeNode(6)
root.right.right = TreeNode(7)
# Inverting the binary tree
inverted_root = invert_tree(root)
# Printing the inverted tree in-order (should print 7 3 6 1 5 2 4)
print_tree(inverted_root)
运行结果:
7 3 6 1 5 2 4
翻转之后的结果:
1
/ \
2 3
/ \ / \
4 5 6 7
5 Question Number 5
There are N rooms in a prison, one for each prisoner, and there are M religions, and each prisoner will follow one of them. If the prisoners in the adjacent room are of the same religion, escape may occur. Please give an O(n) algorithm to find out how many states escape can occur. For example, there are 3 rooms and 2 kinds of religions, then 6 different states escape will occur.
5.1问题重述
要解决这个问题,我们可以考虑每个房间可能的宗教状态,并计算邻近房间宗教相同的情况。对于每个房间,都有M种宗教选择。对于相邻房间可能导致越狱的情况,我们只需要考虑每个房间与其前一个房间是否有相同的宗教。
5.1算法描述(自然语言与伪代码):
自然语言描述:
- 从第一个房间开始,每个房间有M种宗教选择。
- 对于后续的每个房间,如果选择与前一个房间不同的宗教,则不会发生越狱;如果选择相同,则可能发生越狱。
- 对于第一个房间,有M种可能的状态。对于每个后续房间,都有M-1种可能导致越狱的状态(选择与前一个房间相同的宗教)。
- 因此,对于N个房间,越狱的总状态数为M * (M-1)^(N-1)。
伪代码:
function countEscapeStates(N, M):
if N == 1:
return 0 // 只有一个房间时不会发生越狱
escape_states = M * (M - 1)^(N - 1)
return escape_states
5.2 算法正确性证明:
算法的正确性基于组合原则。第一个房间有M种可能性。每个后续房间都可以选择与前一个房间相同的宗教,这样就有M-1种可能性导致越狱。因为房间是线性排列的,所以第一个房间之后的每个房间都只与一个房间相邻,所以这个计算是正确的。
5.3 算法复杂度分析:
该算法的时间复杂度是O(1),因为它只涉及基本的数学运算,不涉及任何循环或递归。空间复杂度同样是O(1),因为算法只需要存储几个整数变量。
对于环形监狱:
在环形监狱的情况下,我们需要调整我们的计算方法来考虑首尾相接的约束。每个囚犯的房间可以被看作是一个节点,整个监狱可以看作是一个环形图。我们的目标是计算所有可能的宗教分配情况,这些情况中任意两个相邻囚犯的宗教都不同。
算法描述:
自然语言描述:
- 第一个囚犯有M种宗教可以选择。
- 第二个到第N-1个囚犯,每个囚犯都有M-1种宗教可以选择,以避免与前一个囚犯选择相同的宗教。
- 对于最后一个囚犯,他不能选择第一个和第N-1个囚犯的宗教,所以如果N>2,他只有M-2种选择。
- 如果只有两个囚犯,第二个囚犯只有M-1种选择,因为他只需要避免与第一个囚犯选择相同的宗教。
- 因此,对于N>2的情况,总的可能状态数为M * (M-1)^(N-2) * (M-2)。对于N=2的情况,总的可能状态数为M * (M-1)。
伪代码:
function countEscapeStatesInCircularPrison(N, M):
if N == 1:
return M // 如果只有一个囚犯,他可以选择任何宗教
if N == 2:
return M * (M - 1) // 如果有两个囚犯,第二个只能选择不同于第一个的宗教
escape_states = M * (M - 1)^(N - 2) * (M - 2)
return escape_states
算法正确性证明:
考虑到环形结构中每个节点(囚犯房间)的两个邻居,我们可以看到第一个囚犯选择后,将影响第二个囚犯的选择,这样一直到最后一个囚犯。由于环形结构,最后一个囚犯的选择又受到第一个囚犯的限制。这种依赖关系形成了一个闭环,因此在计算状态时,我们需要去掉一个额外的自由度来满足首尾相接的约束。
算法复杂度分析:
该算法的时间复杂度为O(1),因为它只涉及一些基本的算术操作,无论N的大小如何,这些操作的数量都是固定的。空间复杂度也为O(1),因为算法只需要存储少量的中间计算结果。