编译原理(第二章3--DFA最小化&双层case和表驱动法)
目录
1. DFA最小化
1.1 为什么要最小化和什么是最小化?
1.2 状态的等价和可区别
1.2.1 状态等价
1.2.2 状态可区别
1.3 如何构建最小化DFA?
1.3.1 最小化DFA思路
1.3.2 最小化DFA步骤
1.3.3 练习
2. 程序实现DFA
2.1 状态转换图实现
2.2 双层case实现
2.3 表驱动实现
3. 小结
1. DFA最小化
1.1 为什么要最小化和什么是最小化?
通过第二章2小节的介绍,我们已经实现了由正则表达式到NFA,NFA到DFA的转化。现在我们手里拿着DFA,下一步应该是构建程序了。
确实如此,但是这里为什么要引入DFA最小化呢?这是因为前面我们通过子集法构建的DFA存在冗余的状态。举个例子,对于a* 来说,我们可以构建如下两个DFA:
 显然,我们更倾向于第二个状态更少的DFA,因为这样我们可以简化我们的程序(状态越多,程序就越会复杂)。
显然,我们更倾向于第二个状态更少的DFA,因为这样我们可以简化我们的程序(状态越多,程序就越会复杂)。
因此我们给出最小化的定义如下:
寻找一个状态数比M少的DFA M’,使得L(M)=L(M’)
意思就是找一个状态数少的DFA,但是它表达的词法特点是不会变的。
1.2 状态的等价和可区别
前面我们介绍了为什么需要DFA最小化,这里为了构建最小化我们引入一些概念来辅助。
1.2.1 状态等价
假设s和t为M的两个状态,满足以下条件则称s和t等价:如果从状态s出发能读出某个字a而停止于终态,那么同样,从t出发也能读出a而停止于终态;反之亦然。
1.2.2 状态可区别
两个状态不等价,则称它们是可区别的。
1.3 如何构建最小化DFA?
1.3.1 最小化DFA思路
构建最小化DFA的思路是这样的:
把待简化的DFA状态集划分为一些不相交的子集,使得任何两个不同子集的状态是可区别的,而同一子集的任何两个状态是等价(等价也就是意味着你找不出一个字使得划分的不同子集中的状态接受后某些到达终态,而某些没有。否则你的最小化DFA就和原来的DFA不一致,这就有问题)。最后,让每个子集选出一个代表,同时消去其他状态。
1.3.2 最小化DFA步骤
- 将非终态和终态划分成不同的子集
- 从对于字母表中的每个字符,让非终态中的每个状态去走一遍,按他们到达的状态属于的子集进行划分,切割成不同的子集,然后对每个新生成的子集重复2
- 从对于字母表中的每个字符,让终态中的每个状态去走一遍,按他们到达的状态属于的子集进行划分,切割成不同的子集,然后对每个新生成的子集重复3
- 形成最终不同的子集,重新编号(注意:含有原初态的子集为简化DFA的初态,含有原终态的子集为简化DFA的终态)
1.3.3 练习
练习一
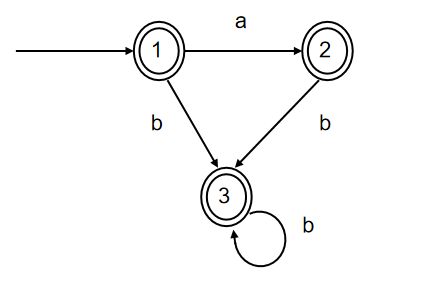
该DFA只有终态集,故首次划分{1,2,3}
对于字符a,状态1经过a可达状态2,而状态2,3均无法识别a
所以按其到达状态的子集 可将{1,2,3}切割成{1}、{2,3}
二次划分得到{1}、{2,3}
对于字符b,{2,3}中:
状态2经过b可达状态3,而状态3属于子集{2,3}
状态3经过b可达状态3,而状态3属于子集{2,3}
到达状态子集相同,因此b也无法切割
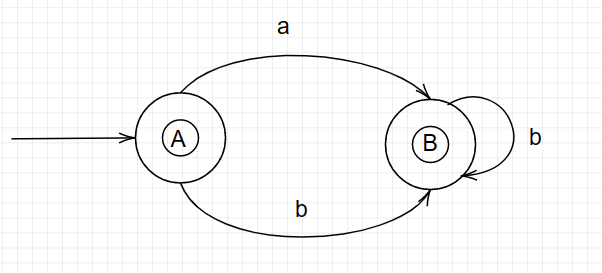
因此我们得到最终的简化DFA:{1}(终态)、{2,3}(终态)。作图如下:
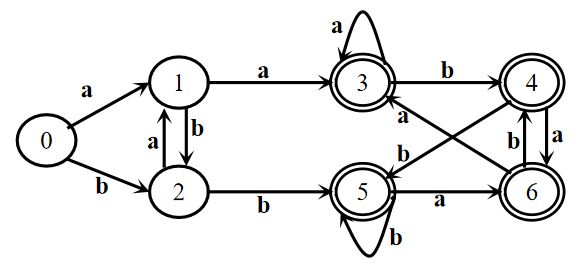
练习二
划分初态集{0,1,2} 终态集{3,4,5,6}
对于初态集{0,1,2}
对于字符a,
状态0接受a到达状态1,而状态1属于{0,1,2}
状态1接受a到达状态3,而状态3属于{3,4,5,6}
状态2接受a到达状态1,而状态1属于{0,1,2}
所以按其到达状态的子集 可将{0,1,2}切割成{1}、{0,2}
二次划分得到{1}、{0,2}。同理{1}已经无法切割,扫描字母表下一个字符,我们继续切割{0,2}
对于字符b,
状态0接受b到达状态2,而状态2属于{0,2}
状态2接受b到达状态5,而状态5属于{3,4,5,6}
所以按其到达状态的子集 可将{0,2}切割成{0}、{2}
三次划分得到{0}、{1}、{2}。初态集切割完成,开始切割终态{3,4,5,6}。
对于字符a,
状态3接受a到达状态3,而状态3属于{3,4,5,6}
状态4接受a到达状态6,而状态6属于{3,4,5,6}
状态5接受a到达状态6,而状态6属于{3,4,5,6}
状态6接受a到达状态3,而状态3属于{3,4,5,6}
因为其到达状态的子集都属于同一个子集无法切割,则继续用b字符切割
对于字符b,
状态3接受b到达状态4,而状态4属于{3,4,5,6}
状态4接受b到达状态5,而状态5属于{3,4,5,6}
状态5接受b到达状态5,而状态5属于{3,4,5,6}
状态6接受b到达状态4,而状态4属于{3,4,5,6}
因为其到达状态的子集都属于同一个子集无法切割
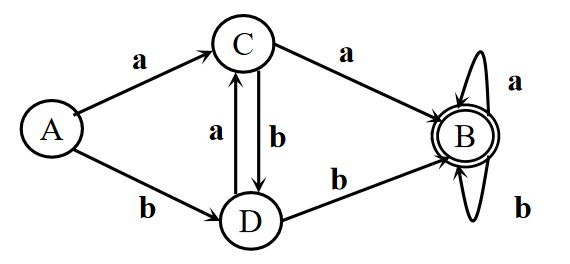
因此我们得到最终的子集:A= {0}(初态)、B = {1}、C = {2}、D = {3,4,5,6} (终态)
故DFA如下:
2. 程序实现DFA
经过大量的介绍铺垫,我们终于来到程序员最感兴趣的地方,那就是用程序去实现我们千辛万苦得到的DFA,从而识别出给定字符中特定的Token。这里主要有三种:状态转换图实现、双层case实现和表驱动实现。这里的重点是后两种。
2.1 状态转换图实现
所谓的状态转换图,其实就是直接根据DFA就开始编写程序。其思想就是大量的if 和while来实现每一种情况判断。
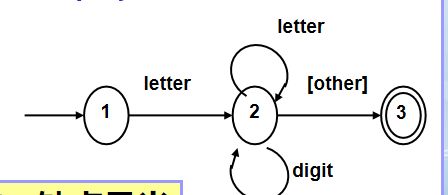
比如对于上面的DFA,我们有伪代码如下 :
//初态开始
if the next character is a letter then
advance the input;//从缓冲区中取出字符,下面的同是如此
while the next character is a letter or a digit do
advance the input;
end while;
accept;
else
{ error or other cases }
end if;
状态转换图实现如果遇到状态较多的情况实现较为复杂,容易出错。
2.2 双层case实现
双层case就是用一个变量state来记录当前状态 ,外层case关注状态转换 ,内层case关注输入字符 其嵌套深度固定为2。
对上述DFA,伪代码书写思路:
(1)初始化状态state为初态
state = 1
(2)设置一个循环,当状态不为除终态的正常状态时一直循环(终态或者错误状态会跳出)
while state = 1 or 2 do:
双层case
end while
if state = 3 then accept else error(3)在循环中双层嵌套case,外部case关注状态,内部case关注输入字符
while state = 1 or 2 do:
case state of:
1:case input character of:
letter:advance the input;//从缓冲区读取字符
state = 2;
other:
state = error;
end case;
2:case input character of:
letter,digit:advance the input;
state = 2;
other:
state = 3;
end case;
end case;
end while
if state = 3 then accept else error我们的编译原理实验中的Tiny编译器源码中的词法扫描就是用双层case实现的
2.3 表驱动实现
表驱动法步骤如下(仍以上述DFA举例):
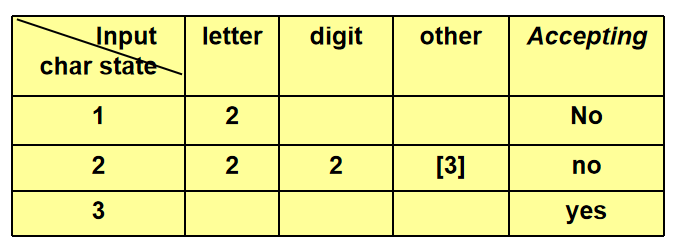
- 将状态图转换成一张二维表
若:
二维数组T记录表格中的转换
二维数组Advance记录是否需要更新输入,考虑字符回退问题
一维数组Accept表示是否为接受状态
- 程序如下:
state = 1
ch = next input character
while not Accept[state] and not Error[state] do:
newstate = T[state,ch]//这里为什么不直接赋值 state,因为我们还要利用原来的state来判断
//是否回退字符
if Advance[state,ch]:
ch = next input character;
state = newstate
end while
if Accept[state] the accept;3. 小结
第二章写了三篇文章,从自然语言到正则表达式、正则表达式到NFA、从NFA到DFA、DFA化简、三种程序实现,我们从头到尾梳理了手工构造词法分析器所用到的理论知识和相关流程,但是注意所有的简述只是针对一个词法特点的,那如何结合多个词法特点的呢?也就是说我们现在已经很轻松地可以构建一个识别C语言标识符的词法扫描器,那如何加入识别C语言的常量、运算符呢?很简单,流程如下:
(1)对每一个词法特点构建各自的NFA
(2)构建一个新的初态X,用将各个NFA和新的初态X连接起来形成一个新的NFA
(3)NFA转DFA,然后最小化DFA
(4)编码写程序
第二章到此结束。