【MATLAB实验】MATLAB图形绘制相关函数与定积分计算

Matlab中的图形

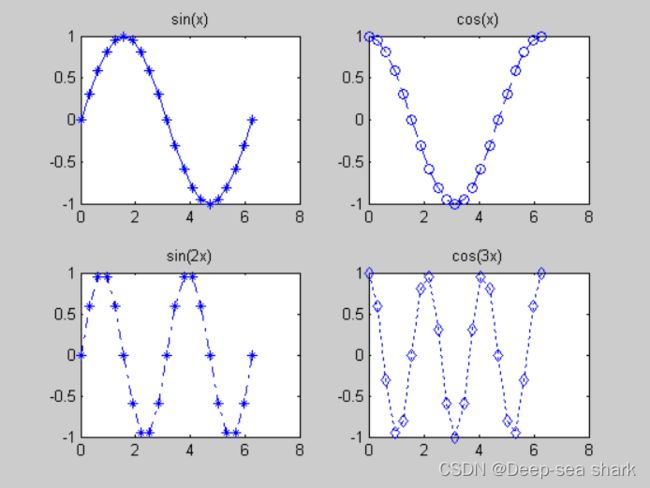
x=0:0.1*pi:2*pi;
subplot(2,2,1)
plot(x,sin(x),'-*')
title('sin(x)');
subplot(2,2,2)
plot(x,cos(x),'--o');
title('cos(x)');
subplot(2,2,3)
plot(x,sin(2*x),'-.*');
title('sin(2x)');
subplot(2,2,4)
plot(x,cos(3*x),':d');
title('cos(3x)');

对数图、极坐标图及条形图

1. loglog表示用log10-log10标度绘图
2. semilogx用半对数坐标绘图，x轴是log10，y是线性的
3. semilogy用半对数坐标绘图，y轴是log10，x是线性的
4. bar(x)显示x向量元素的条形图，bar不接受多变量
5. hist绘制统计频率直方图
6. fplot(fname,lims)绘制fname指定函数图形
7. polar(theta,rho)使用相角为theta为极坐标形式绘图，相应半径为rho，其次可以使用grid命令画出极坐标网格
8. histfit(data,nbins)绘制统计直方图与其正态分布拟合曲线

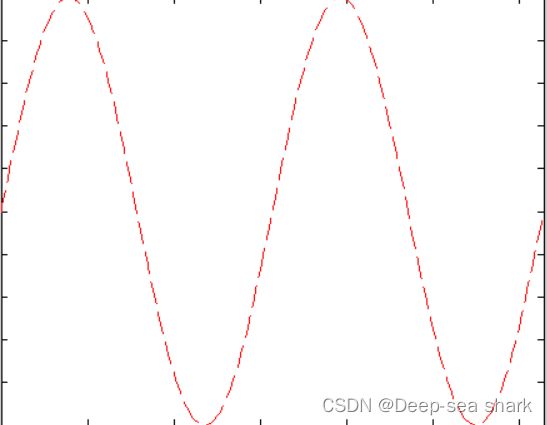
fplot('sin',[0 4*pi],'--r')

matlab命令	作用
title	图形标题
xlabel	x坐标轴标注
ylabel	y坐标轴标注
text	标注数据点
grid	给图形加上网格
hold	保持图形窗口的图形

填充图

利用二维绘图函数patch，我们可以绘制填充图，绘制填充图的另一个函数为fill

下面的例子绘制出了hunps（一个演示函数）在指定区域内的函数图形

fplot('humps',[0,2],'b')
hold on%表示保持图形窗口的图形
patch([0.5 0.5:0.001:1 1],[0 humps(0.5:0.001:1) 0],'y')
hold off
title('A region under an interesting function')
grid

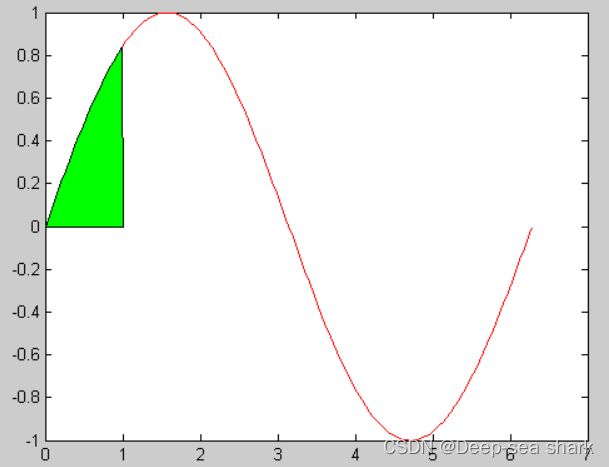
x=0:pi/60:2*pi;
y=sin(x);
x1=0:pi/60:1;
y1=sin(x1);
plot(x,y,'-r');
hold on
fill([x1,1],[y1,0],'g')

三维作图

• mes(z)语句

x=-8:0.5:8;
y=x';
x=ones(size(y))*x;
y=y*ones(size(y))';
R=sqrt(x.^2+y.^2)+eps;
z=sin(R)./R;
mesh(z)
%前四句可以用[x,y]=meshgrid(-8:0.5:8)

与mesh相关的几个函数

1. meshc与函数mesh的调用方式相同，只是该函数在mesh的基础上又增加了绘制相应等高线的功能，下面来看一个meshc的例子

   [x,y]=meshgrid([-4:0.5:4]);
   z=sqrt(x.^2+y.^2);
   meshc(z)
   

   

   地面上的圆圈就是上面图形的等高线。

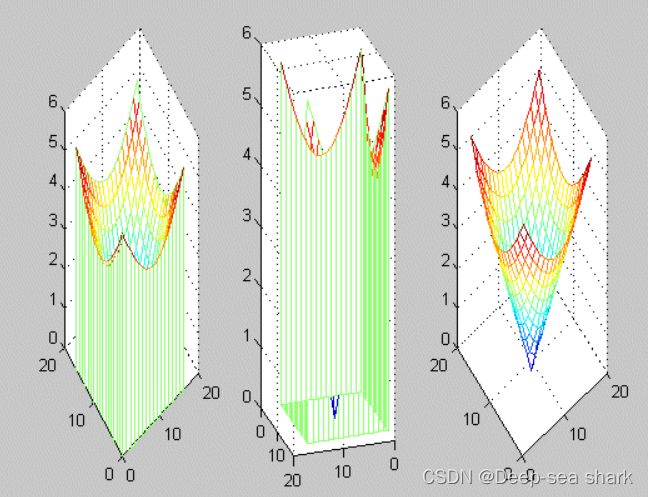
2. meshz与mesh的调用方式也相同，不同的是该函数是在mesh函数的作用之上增加了屏蔽作用，即增加了边界屏蔽

   [x,y]=meshgrid([-4:0.5:4]);
   z=sqrt(x.^2+y.^2);
   subplot(1,3,1)
   meshz(z)
   subplot(1,3,2)
   meshz(z)
   subplot(1,3,3)
   mesh(z)
   %subplot的用法subplot(几行，几列，目前是这行的第几个)
   

   

3. 其他几个三维绘图函数

   • 在matlab中有一个专门绘制球体的函数sphere，调用格式如下

   [x,y,z]]=sphere(n)%此函数生成一个（n+1）×（n+1）阶的矩阵，在利用surf(x,y,z)可以生成单位球面
   [x,y,z]=sphere%此形式默认n值为20
   sphere(n)%只绘制球面，不返回值
   %运行下面程序
   sphere(30);
   axis square;
   

   

   • surf函数也是matlab中常用的三维绘图函数，调用格式如下：

     surf(x,y,z,c)

     看下面例子：

     [a,b,c]=sphere(40);
     t=abs(c);%求绝对值
     surf(a,b,c,t);
     axis equal
     colormap('hot')
     

   

   图形的控制与修饰

   matlab命令	功能
   axis([xmin,xmax,ymin,ymax,zmin,zmax])	控制坐标轴的范围
   axis auto	自动模式使得坐标图形满足图中一切元素的范围
   axis equal	严格控制坐标的分度使其相等
   axis square	使绘制区为正方形
   axis on	恢复对坐标轴的一切设置
   axis off	取消对坐标轴的一切设置
   axiso munual	以当前的坐标限制图形的绘制
   grid off	取消网格
   xlabel(‘标注文本’，‘属性1’，‘属性2’，‘属性3’，‘属性4’…)	这里属性可以包括字体大小，字体名，字体粗细

   • 统计回归图

     1. 已知下列点，求其回归直线，并计算最小误差平方和

        x	0.1	0.11	0.12	0.13	0.14	0.15	0.16	0.17	0.18	0.20	0.21	0.23
        y	42	43.5	45	45.5	45	47.5	49	53	50	55	55	60

        参考如下程序

        x=[0.1 0.11 0.12 0.13 0.14 0.15 0.16 0.17 0.18 0.20 0.21 0.23];
        y=[42 43.5 45 45.5 45 47.5 49 53 50 55 55 60];
        n=length(x);
        xb=means(x);
        yb=means(y);
        x2b=sum(x.^2)/n;
        xyb=x&y'/n;
        b=(xb*yb-xyb)/(xb^2-x2b);
        a=yb-b*xb;
        y1=a+b.*x;
        plot(x,y,'*',x,y1);
        serror=sum((y-y1).^2)
        

        

Matlab符号运算

matlab的常见6大符号运算

1. 因式分解

   syms x
   f=x^6+1;
   s=factor(f)
   %结果为
   s=(x^2+1)*(x^4-x^2+1)
   

2. 计算极限
   $$(1)L=\underset{x\to 0}{\lim }\frac{ln(x+h)-ln(x)}{h}$$

   $$(2)M=\underset{n\to \infty }{\lim }(1-\frac{x}{n}{)}^n$$

   syms h n x
   L=limit('(log(x+h)-log(x))/h',h,0)%单引号可以省略掉
   M=limit('(1-x/n)^n',n,inf)
   %结果为
   L=1/x
   M=exp(-x)
   
   

3. 计算导数
   $$y=sinax，求A=\frac{dy}{dx},B=\frac{dy}{da},C=\frac{d^{2}y}{d^{2}x}$$

   syms a x;   y=sin(a*x);
   A=diff(y,x)
   B=diff(y,a)
   C=diff(y,x,2)
   

4. 计算不定积分、定积分、反常积分

   $$I=\int \frac{x^2+1}{(x^2-2x+2{)}^2}dx$$
   $$J={\int }_0^{\pi /2}\frac{cosx}{sinx+cosx}dx$$
   $$K={\int }_0^{\infty }{e}^{-x^2}dx$$

   syms x
   f=(x^2+1)/(x^2-2*x+2)^2;
   g=cos(x)/(sin(x)+cos(x));
   h=exp(-x^2);
   I=int(f)
   J=int(g,0,pi/2)
   K=(h,0,inf)
   

5. 求和符号
   $$求级数\sum _{n=1}^{\infty }\frac{1}{n^2}的和S,以及前10项的部分和S1.$$

   syms n
   S=symsum(1/n^2,1,inf)
   S1=symsum(1/n^2,1,10)
   %S = 1/6*pi^2
   %S1 = 1968329/1270080
   

   $$重要说明：当求函数项级数\sum _{n=1}^{\infty }\frac{x}{n^2}时可用命令$$

   syms n x
   S2=symsum(x/n^2,n,1,inf)
   %S2 = 1/6*x*pi^2
   

6. 解代数方程和常微分方程

   %利用符号表达式求解代数方程所需要的函数为solve(f),即解符号方程式f.
   %例如解一元二次方程式a*x^2+b*x+c的根
   f=sym('a*x^2+b*x+c')或f='a*x^2+b*x+c'
   solve(f)
   %{ans =
    1/2/a*(-b+(b^2-4*a*c)^(1/2))
    1/2/a*(-b-(b^2-4*a*c)^(1/2))
    %}
    solve(f,a)
    
   %{ans =
   -(b*x+c)/x^2
   %}
   

   利用符号表达式可以求解微分方程的解析解，所需函数为dsolve(f)

   使用格式如下：

   dsolve('equation 1','equation 2',...)
   

   $$(1)求微分方程y^{\prime }=x的通解:symsxydsolve{(}^{\prime }Dy=x^{\prime }{,}^{\prime }{x}^{\prime })$$

   matlab特殊函数与图形

• 相关函数命令即简介

  函数	功能
  linewidth	指定线条的粗细
  markeredgecolor	标记的边缘色
  markerfacecolor	标记的表面色
  markersize	标记的大小

  plot(x,y,s)
  %x横坐标，y纵坐标，s图像属性
  x=-pi:pi/10:pi;
  y=sin(x);
  plot(x,y,'--rh','linewidth',2,'markeredgecolor','b','markerfacecolor','g')
  %如果需要在一个坐标系中画几个函数
  plot(x1,y1,s1,x2,y2,s2,...)
  

  

• 空间曲线作图函数

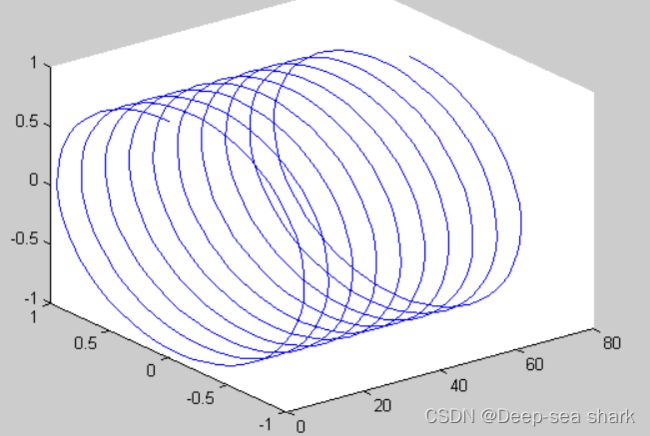
  %plot3与plot相比，只是多了一个维数而已，调用格式如下
  plot(x,y,z,s)
  
  x=0:pi/30:20*pi;
  y=sin(x);
  z=cos(x);
  plot3(x,y,z)
  

  

  得到三维螺旋曲线.

• 空间曲面作图函数

  1. mesh：绘制彩色网格面图形

  2. surf：在矩形区域内显示三维带阴影的曲面图，调用格式与mesh相似

  3. ezmesh：用符号函数作三维曲面网格图

     %调用格式
     ezmesh(x,y,z)
     %或者
     ezmesh(x,y,z,[smin,smax,tmin,tmax])
     

  4. ezsurf：三维曲面图，调用格式与ezmesh类似

  5. sphere：画球体命令

  6. meshgrid：

     [x,y]=meshgrid(m,n)
     %m,n为给定向量，可以定义网格划分区域和划分方法。矩阵x和矩阵y是网格划分过后的数据矩阵
     
     axis equal %控制各个坐标轴的分度，使其相等
     colormap %设置绘图颜色
     
     grid %网格函数  grid on 添加网格  grid off取消网格
     
     find %找出符合条件的元素在数组中的位置
     %例如：
     a=[4 5 78 121 4 665 225 4 1];
     b=find(a>7)
     

     利用plot函数在一个坐标系中画几个函数图像，采用不同颜色、线型、标记

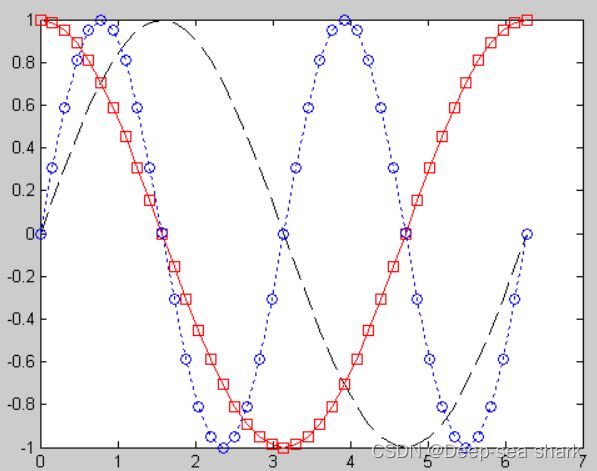
     t=0:pi/20:2*pi;
     x=sin(t);
     y=cos(t);
     z=sin(2*t);
     plot(t,x,'--k',t,y,'-rs',t,z,':bo')
     

     

定积分的近似计算

• 相关函数命令即及简介

  命令	功能
  sum	求数组的和
  double()	若输入的是字符型转化为相应的ASCII码，输入的是整型转化为相应的实型数值
  quad()	抛物线法求数组积分
  trapz()	梯形法求数值积分
  dblquad()	抛物线法求二重积分数值
  fprintf()	把数据写入指定文件
  int(f,v,a,b)	求f关于v积分，积分区间由a到b
  subs(f,‘x’,a)	将a的值赋给符号表达式f中的x，并计算出值，若简单的使用subs(f),则将f的所有符号变量用有可能的数值带入，并计算出此值

  quad(fun,a,b)%注意此处的fun是函数，并且为数值形式，所以使用*、/、^等运算符时还要在其前面加上小数点
  
  %例1：
  
  

  常微分方程

$$\begin{array}{rl}& 在t\in [0,100]时，求\{\begin{array}{l}\frac{dx}{dt}=-y-z\\ \frac{dy}{dt}=x+0.2y\\ \frac{dz}{dt}=0.2-5.7z+zx\end{array}，\\ & 满足x(0)=0,y(0)=0.z(0)=0的数值解。\end{array}$$

求解过程如下：(1)建立表示微分方程的自定义函数，建立自定义函数名为rossler.m,内容为：

function dx = rossler(t,x)
     dx=[-x(2)-x(3);x(1)+0.2*x(2);0.2+(x(1)-5.7)*x(3)];

建立一个命名文件rossler1.m，以调用ode45函数对微分方程进行数值求解。

clf
    x0=[0;0;0];
    [t,y]=ode45('rossler',[0,100],x0);
    subplot(2,1,1)
    plot(t,y(:,1),'r--',t,y(:,2),'k-',t,y(:,3),'b:');
    subplot(2,1,2)
    plot3(y(:,1),y(:,2),y(:,3))