滑动窗口算法
长度最小的子数组(mid)
题目链接:长度最小的子数组
算法思路
解法1:暴力枚举(超时)
「从前往后」枚举数组中的任意⼀个元素,把它当成起始位置。然后从这个「起始位置开始,然后寻找⼀段最短的区间,使得这段区间的和「⼤于等于」⽬标值。将所有元素作为起始位置所得的结果中,找到「最⼩值」即可。
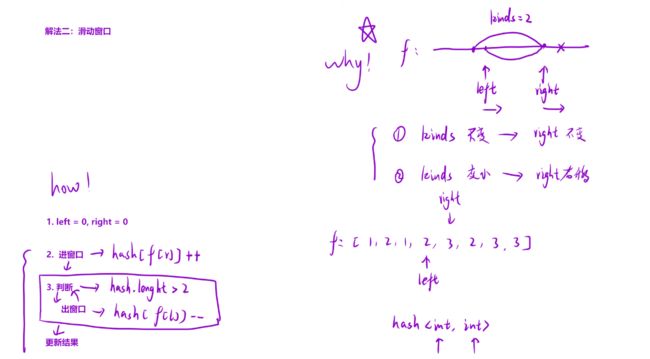
解法2:滑动窗口
由于此问题分析的对象是「⼀段连续的区间」,因此可以考虑「滑动窗⼝」的思想来解这道题。让滑动窗⼝满⾜:从 i 位置开始,窗⼝内所有元素的和⼩于 target (那么当窗⼝内元素之和第⼀次⼤于等于⽬标值的时候,就是 i 位置开始,满⾜条件的最⼩⻓度)。做法:将右端元素划⼊窗⼝中,统计出此时窗⼝内元素的和:
- 如果窗⼝内元素之和⼤于等于 target :更新结果,并且将左端元素划出去的同时继续判断是否满⾜条件并更新结果(因为左端元素可能很⼩,划出去之后依旧满⾜条件)
- 如果窗⼝内元素之和不满⾜条件: right++ ,另下⼀个元素进⼊窗⼝。
- 这个窗⼝寻找的是:以当前窗⼝最左侧元素(记为 left1)为基准,符合条件的情况。也就是在这道题中,从 left1开始,满⾜区间和 sum >= target 时的最右侧(记为right1)能到哪⾥。
- 我们既然已经找到从 left1 开始的最优的区间,那么就可以⼤胆舍去 left1 。但是如 果继续像⽅法⼀⼀样,重新开始统计第⼆个元素( left2 )往后的和,势必会有⼤量重复的计算(因为我们在求第⼀段区间的时候,已经算出很多元素的和了,这些和是可以在算下次区间和的时候⽤上的)。
- 此时, rigth1 的作⽤就体现出来了,我们只需将 left1 这个值从 sum 中剔除。从 right1 这个元素开始,往后找满⾜ left2 元素的区间(此时 right1 也有可能是满 ⾜的,因为 left1 可能很⼩。 sum 剔除掉 left1 之后,依旧满⾜⼤于等于 target )。这样我们就能省掉⼤量重复的计算。
时间复杂度:虽然代码是两层循环,但是我们的 left 指针和 right 指针都是不回退的,两者最多都往后移动 n 次。因此时间复杂度是 O(N)
代码
class Solution {
public int minSubArrayLen(int target, int[] nums) {
int n = nums.length, sum = 0, len = Integer.MAX_VALUE;
for(int left = 0, right = 0; right < n; right++){
sum += nums[right]; // 进窗⼝
while(sum >= target) // 判断,并且要循环,因为左边元素可能很小,还符合条件
{
len = Math.min(len, right - left + 1); // 更新结果
sum -= nums[left++]; // 出窗⼝
}
}
return len == Integer.MAX_VALUE ? 0 : len;
}
}
无重复字符的最长子串(mid)
题目链接:无重复字符的最长子串
算法思路
研究的对象依旧是⼀段连续的区间,因此继续使⽤「滑动窗⼝」思想来优化。 让滑动窗⼝满⾜:窗⼝内所有元素都是不重复的。
做法:右端元素 ch 进⼊窗⼝的时候,哈希表统计这个字符的频次:
- 如果这个字符出现的频次超过 1 ,说明窗⼝内有重复元素,那么就从左侧开始划出窗口,直到 ch 这个元素的频次变为 1 ,然后再更新结果。
- 如果没有超过 1 ,说明当前窗⼝没有重复元素,可以直接更新结果
代码
class Solution {
public int lengthOfLongestSubstring(String s) {
int[] hash = new int [128]; // 用来去重
int result = 0;
int len = 0;
for(int left = 0, right = 0; right < s.length(); right++) {
int tmp = s.charAt(right);
len++;// 进窗口
hash[tmp]++;
while(hash[tmp] > 1) {
// 出现重复的字符,出窗口
hash[s.charAt(left) ]--;
left++;
len--;
}
// 更新结果
result = Math.max(result, len);
}
return result;
}
}
最大连续1的个数Ⅲ(mid)
题目链接:最大连续1的个数Ⅲ
算法思路
不要去想怎么翻转,不要把问题想的很复杂,这道题的结果⽆⾮就是⼀段连续的 1 中间塞了 k个 0 嘛。
因此,我们可以把问题转化成:求数组中⼀段最⻓的连续区间,要求这段区间内 0 的个数不超过 k 个。
既然是连续区间,可以考虑使⽤「滑动窗⼝」来解决问题。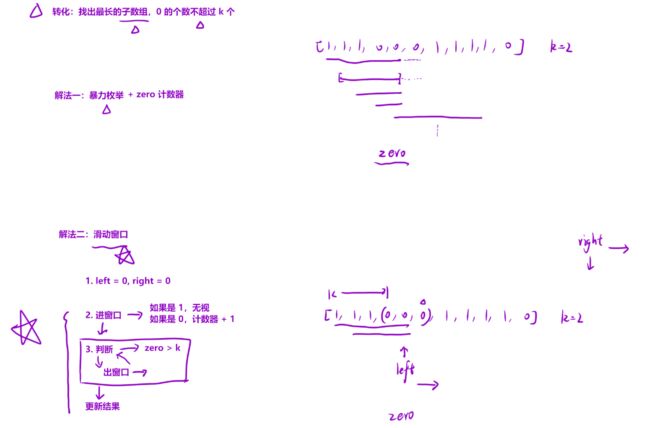
代码
class Solution {
public int longestOnes(int[] nums, int k) {
int result = 0;
for(int left = 0, right = 0, zero = 0; right < nums.length; right++) {
// 进窗口
if(nums[right] == 0) {
zero++;
}
// 判断0的个数是否大于k
while(zero > k) {
if(nums[left] == 0) {
zero--;
}
// 出窗口
left++;
}
// 更新结果
result = Math.max(result, right - left + 1);
}
return result;
}
}
将x减到0的最小操作数(mid)
题目链接:将x减到0的最小操作数
算法思路:
题⽬要求的是数组「左端+右端」两段连续的、和为 x 的最短数组,信息量稍微多⼀些,不易理清思路;我们可以转化成求数组内⼀段连续的、和为 sum(nums) - x 的最⻓数组。此时,就是熟悉的滑动窗口问题了。
代码
class Solution {
public int minOperations(int[] nums, int x) {
int sum = 0;
for(int i = 0; i < nums.length; i++) {
sum += nums[i];
}
sum -= x;
// 细节处理
if(sum < 0) {
return - 1;
}
int result = -1;
for(int left = 0, right = 0; right < nums.length; right++) {
// 进窗口
sum -= nums[right];
// 判断
while(sum < 0) {
sum += nums[left];
left++; // 出窗口
}
// 更新
if(sum == 0) {
result = Math.max(result, right - left + 1);
}
}
return result == -1 ? -1 : nums.length - result;
}
}
水果成篮(mid)
题目链接:水果成篮
算法思路:
研究的对象是⼀段连续的区间,可以使⽤「滑动窗⼝」思想来解决问题。
让滑动窗⼝满⾜:窗⼝内⽔果的种类只有两种。
做法:右端⽔果进⼊窗⼝的时候,⽤哈希表统计这个⽔果的频次。这个⽔果进来后,判断哈希表的大小:
- 如果大小超过 2:说明窗⼝内⽔果种类超过了两种。那么就从左侧开始依次将⽔果划出窗⼝,直到哈希表的大小小于等于 2,然后更新结果;
- 如果没有超过 2,说明当前窗⼝内⽔果的种类不超过两种,直接更新结果 retsult。
代码:
class Solution {
public int totalFruit(int[] fruits) {
Map<Integer,Integer> hash = new HashMap<>(2);
int result = 0;
for(int left = 0, right = 0; right < fruits.length; right++) {
// 进窗口
hash.put(fruits[right], hash.getOrDefault(fruits[right], 0) + 1);
// 判断
while(hash.size() > 2) {
// 出窗口
hash.put(fruits[left], hash.get(fruits[left]) - 1);
if(hash.get(fruits[left]) == 0) {
hash.remove(fruits[left]);
}
left++;
}
// 更新结果
result = Math.max(result, right - left + 1);
}
return result;
}
}
找到字符串中所有的字母异位词(mid)
题目链接:找到字符串中所有字母异位词
算法思路:
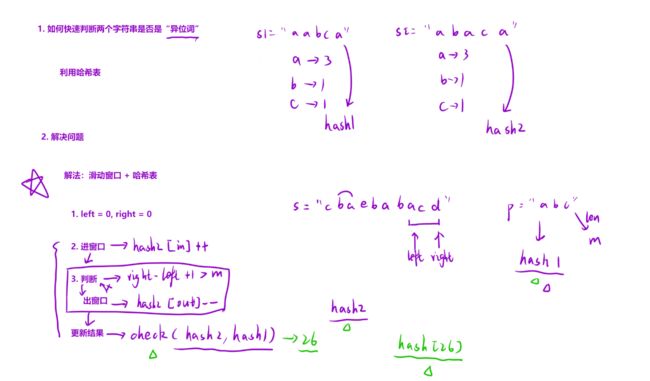
- 因为字符串 p 的异位词的⻓度⼀定与字符串 p 的⻓度相同,所以我们可以在字符串 s 中构造⼀个⻓度为与字符串 p 的⻓度相同的滑动窗⼝,并在滑动中维护窗⼝中每种字⺟的数量;
- 当窗⼝中每种字⺟的数量与字符串 p 中每种字⺟的数量相同时,则说明当前窗⼝为字符串 p的异位词;
- 因此可以⽤两个⼤⼩为 26 的数组来模拟哈希表,⼀个来保存 s 中的⼦串每个字符出现的个数,另⼀个来保存 p 中每⼀个字符出现的个数。这样就能判断两个串是否是异位词。
代码:
class Solution {
public List<Integer> findAnagrams(String s, String p) {
char[] ss = s.toCharArray();
char[] pp = p.toCharArray();
int len = 0;
int[] hash1 = new int[26];
for(int i = 0; i < pp.length; i++) {
hash1[pp[i] - 'a']++;
}
int[] hash2 = new int[26];
List<Integer> result = new ArrayList<>();
for(int left = 0, right = 0; right < ss.length; right++) {
// 进窗口
hash2[ss[right] - 'a']++;
len++;
// 判断
while(len == p.length()) {
// 更新结果
if(isEqual(hash1, hash2)) {
result.add(left);
}
// 出窗口
hash2[ss[left] - 'a']--;
left++;
len--;
}
}
return result;
}
private boolean isEqual(int[] hash1, int[] hash2) {
for(int i = 0; i < hash1.length; i++) {
if(hash1[i] != hash2[i]) {
return false;
}
}
return true;
}
}
优化:
class Solution
{
public List<Integer> findAnagrams(String ss, String pp)
{
List<Integer> ret = new ArrayList<Integer>();
char[] s = ss.toCharArray();
char[] p = pp.toCharArray();
int[] hash1 = new int[26]; // 统计字符串 p 中每⼀个字符出现的个数
for(char ch : p) hash1[ch - 'a']++;
int[] hash2 = new int[26]; // 统计窗⼝中每⼀个字符出现的个数
int m = p.length;
for(int left = 0, right = 0, count = 0; right < s.length; right++)
{
char in = s[right];
// 进窗⼝ + 维护 count
if(++hash2[in - 'a'] <= hash1[in - 'a']) count++;
if(right - left + 1 > m) // 判断
{
char out = s[left++];
// 出窗⼝ + 维护 count
if(hash2[out - 'a']-- <= hash1[out - 'a']) count--;
}
// 更新结果
if(count == m) ret.add(left);
}
return ret;
}
}
串联所有单词的子串(hard)
题目链接:串联所有单词的子串
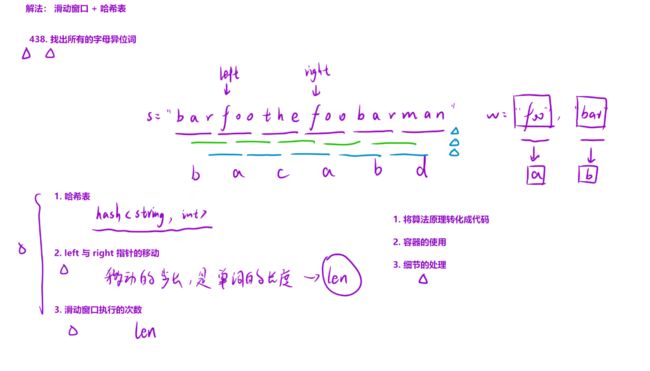
算法思路
代码
class Solution {
public List<Integer> findSubstring(String s, String[] words) {
List<Integer> result = new ArrayList<>();
HashMap<String, Integer> hash1 = new HashMap<>();
for(String x : words) {
hash1.put(x, hash1.getOrDefault(x, 0) + 1);
}
int len = words[0].length();
int num = words.length;
// 执行几次滑动窗口
for(int i = 0; i < len; i++) {
HashMap<String, Integer> hash2 = new HashMap<>();
// 注意边界
for(int left = i, right = i, count = 0; right + len <= s.length(); right += len) {
// 进窗口
String in = s.substring(right, right + len);
hash2.put(in , hash2.getOrDefault(in, 0) + 1);
// count用来维护有效个数
if(hash2.get(in) <= hash1.getOrDefault(in, 0)) count++;
// 判断
if(right - left + 1 > len * num) {
// 出窗口
String out = s.substring(left, left + len);
if(hash2.get(out) <= hash1.getOrDefault(out, 0)) count--;
hash2.put(out, hash2.get(out) - 1);
left += len;
}
// 更新结果
if(count == num) {
result.add(left);
}
}
}
return result;
}
}
最小覆盖子串
题目链接:最小覆盖子串
算法思路:
代码:
class Solution {
public String minWindow(String s, String t) {
StringBuilder sb = new StringBuilder();
char[] tt = t.toCharArray();
int[] hash1 = new int[128];
int kind = 0;// 统计有效字符有多少种
for(char x : tt) {
if(hash1[x]++ == 0) {
kind++;
}
}
char[] ss = s.toCharArray();
int[] hash2 = new int[128];
int minlen = Integer.MAX_VALUE, begin = -1;
for(int left = 0, right = 0, count = 0; right < ss.length; right++) {
// 进窗口
char in = ss[right];
hash2[in]++;
if(hash2[in] == hash1[in]) count++;
while(count == kind) {
// 更新结果
if(right - left + 1 < minlen ) {
minlen = right - left + 1;
begin = left;
}
// 出窗口
char out = ss[left++];
if(hash2[out]-- == hash1[out]) count--;
}
}
if(begin == -1) return new String();
else return s.substring(begin, begin + minlen);
}
}