【数据结构与算法】【C++】图的邻接表实验报告（六）

目录

阅读建议：

一、实验目的

二、实验内容

三、实验过程

四、代码结构

五、测试结果

---

阅读建议：

1.实验的软硬件环境要求：

（1）硬件环境要求：PC机
（2）软件环境要求：Windows 环境下的 Microsoft Visual Studio

2.该实验采用了头文件（.h）和源文件（.cpp）相结合的形式。

---

一、实验目的

1. 熟练掌握图的邻接表存储结构的实现； 

2. 熟练掌握基于邻接表的图的基本操作算法实现；

3. 灵活使用有向图来解决具体的问题。

---

二、实验内容

1. 定义有向图的邻接表类，封装图的基本操作算法，包括：

        （1）创建、销毁邻接表存储的图

        （2）深度优先和广度优先遍历图

        （3）增加一个顶点

        （4）增加一条弧

        （5）删除一条弧

2. 对建立的有向图进行拓扑排序，输出拓扑序列。

---

三、实验过程

1.定义边表结点。

struct EdgeNode
{
	int adjvex;  // 邻接点域
	EdgeNode* next;
};

2.定义顶点表结点。

template
struct VertexNode
{
	T vertex;
	EdgeNode* firstEdge;
};

3.构造函数。

工作原理：

1. 初始化:

   • vertexNum 被设置为 n，表示顶点的数量。
   • edgeNum 被设置为 e，表示边的数量。

2. 初始化顶点表:

   • 使用一个循环，对每一个顶点进行初始化。循环从0到vertexNum-1。
   • 对于每个顶点，首先从标准输入读取一个整数并将其存储在变量 ai 中。这个整数表示该顶点的输入值。
   • 将 ai 赋值给 adjlist[i].in，表示顶点i的输入值。
   • 将数组 a 中与顶点i对应的值赋给 adjlist[i].vertex，表示顶点i的值。
   • 将 nullptr 赋给 adjlist[i].firstEdge，表示该顶点的边表初始为空。

3. 初始化边表:

   • 使用一个循环，对每一条边进行初始化。循环从0到edgeNum-1。
   • 对于每条边，首先从标准输入读取两个整数，分别表示这条边的两个顶点的编号。
   • 创建一个新的边表结点 s。
   • 将边所依附的第二个顶点的编号（即j）赋值给 s->adjvex。
   • 将结点 s 插入到顶点i的边表中，使其成为表头。这意味着边(i, j)是第一个与顶点i关联的边。

template
ALGraph::ALGraph(T a[], int n, int e)
{
	vertexNum = n;
	edgeNum = e;
	// 输入顶点信息，初始化顶点表
	for (int i = 0; i < vertexNum; i++) {
		int ai;
		cin >> ai;
		adjlist[i].in = ai;
		adjlist[i].vertex = a[i];
		adjlist[i].firstEdge = nullptr;
	}
	// 依次输入每一条边
	for (int k = 0; k < edgeNum; k++) {
		int i, j;
		// 输入边所依附的两个顶点的编号
		cin >> i >> j;
		// 生成一个边表结点s
		EdgeNode* s = new EdgeNode;
		s->adjvex = j;
		// 将结点s插入表头
		s->next = adjlist[i].firstEdge;
		adjlist[i].firstEdge = s;
	}
}

4.析构函数。

工作原理：

1. 使用一个循环，遍历每个顶点的边表。循环从0到vertexNum-1。
2. 对于每个顶点的边表，首先获取其第一个边表结点 p。
3. 使用一个while循环，遍历该顶点的整个边表。循环会一直执行，直到指针 p 指向 nullptr，即边表为空。
   • 在while循环内部，首先将当前结点 q 保存为一个临时指针。
   • 然后将指针 p 移动到下一个结点。
   • 使用 delete 操作符释放当前结点 q 的内存空间。
4. 完成释放内存后，指针 p 将指向边表的末尾，即 nullptr。

template
ALGraph::~ALGraph()
{
	// 释放边表结点的内存空间
	for (int i = 0; i < vertexNum; i++) {
		EdgeNode *p = adjlist[i].firstEdge;
		while (p != nullptr) {
			EdgeNode* q = p;
			p = p->next;
			delete q;
		}
	}
}

5.增加一个顶点。

工作原理：

1. 检查图是否已满:

   • 如果 vertexNum（表示已添加的顶点数量）已经达到了 MaxSize（表示图的最大容量），则输出“【图已满】”并结束函数。这意味着图已无法再添加新的顶点。

2. 初始化新顶点:

   • 将新顶点的值赋给 adjlist[vertexNum].vertex。
   • 将新顶点的输入值赋给 adjlist[vertexNum].in，并初始化为0。
   • 将 nullptr 赋给 adjlist[vertexNum].firstEdge，表示新顶点的边表初始为空。

3. 增加顶点数量:

   • 将 vertexNum 增加1，表示图中已添加了一个新的顶点。

template
void ALGraph::AddVertex(T v)
{
	if (vertexNum >= MaxSize) {
		cout << "【图已满】";
		return;
	}
	adjlist[vertexNum].vertex = v;
	adjlist[vertexNum].in = 0;
	adjlist[vertexNum].firstEdge = nullptr;
	vertexNum++;
}

6.增加一条弧。

工作原理：

1. 检查顶点编号的有效性:

   • 如果起点顶点编号 i 或终点顶点编号 j 大于等于 vertexNum（表示已添加的顶点数量）或小于0，则输出“【顶点编号无效，无法添加】”并结束函数。这表示提供的顶点编号是无效的，因此无法添加边。

2. 创建新的边表结点:

   • 创建一个新的边表结点 s。
   • 将终点顶点的编号 j 赋给 s->adjvex，表示这条边连接了顶点i和j。

3. 将新结点插入边表:

   • 将新结点 s 的指针赋值给 adjlist[i].firstEdge，表示边(i, j)是顶点i的第一个关联边。
   • 如果顶点i的边表中已经有其他结点，则将新结点插入到链表的头部，确保新添加的边在遍历时能被优先处理。

4. 增加边数量:

   • 将 edgeNum 增加1，表示图中已添加了一条新的边。

template
void ALGraph::AddEdge(int i, int j)
{
	if (i >= vertexNum || j >= vertexNum || i < 0 || j < 0) {
		cout << "【顶点编号无效，无法添加】";
		return;
	}
	EdgeNode* s = new EdgeNode;
	s->adjvex = j;
	s->next = adjlist[i].firstEdge;
	adjlist[i].firstEdge = s;
	edgeNum++;
}

7.删除一条弧。

工作原理：

1. 检查顶点编号的有效性:

   • 如果起点顶点编号 i 或终点顶点编号 j 大于等于 vertexNum（表示已添加的顶点数量）或小于0，则输出“【顶点编号无效，无法删除】”并结束函数。这表示提供的顶点编号是无效的，因此无法删除边。

2. 查找要删除的边:

   • 获取起点顶点i的边表头结点 p。
   • 使用一个循环，遍历边表直到找到与终点j匹配的边或到达链表末尾。在每次循环中，保存当前结点 p 到 q，并将结点指针向前移动。
   • 如果在遍历完整个链表后没有找到与终点j匹配的边，则输出“【该弧不存在】”并结束函数。这表示提供的边在图中不存在，因此无法删除。

3. 删除边:

   • 如果找到了要删除的边，并且它是链表的第一个结点（即链表的头部），则将链表的头部指针更新为下一个结点。
   • 否则，将找到的结点前一个结点的next指针指向找到结点的下一个结点，从而跳过找到的结点。

4. 释放内存:

   • 使用 delete 操作符释放找到的结点的内存空间。

5. 减少边的数量:

   • 将 edgeNum 减少1，表示图中已删除了一条边。

template
void ALGraph::DeleteEdge(int i, int j)
{
	if (i >= vertexNum || j >= vertexNum || i < 0 || j < 0) {
		cout << "【顶点编号无效，无法删除】";
		return;
	}
	EdgeNode* p = adjlist[i].firstEdge;
	EdgeNode* q = nullptr;
	while (p != nullptr && p->adjvex != j) {
		q = p;
		p = p->next;
	}
	if (p == nullptr) {
		cout << "【该弧不存在】";
		return;
	}
	if (q == nullptr) {
		adjlist[i].firstEdge = p->next;
	}else {
		q->next = p->next;
	}
	delete p;
	edgeNum--;
}

8.深度优先遍历。

工作原理：

1. 输出当前顶点:

   • 输出当前顶点v的值。

2. 标记当前顶点为已访问:

   • 将 visited[v] 设置为1，表示顶点v已被访问过。

3. 初始化工作指针:

   • 将工作指针 p 初始化为指向顶点v的边表的头部。

4. 遍历顶点v的邻接点:

   • 使用一个循环，遍历顶点v的所有邻接点。在每次循环中，保存当前结点 p 到 q，并将结点指针向前移动。
   • 对于每个邻接点j，如果邻接点j尚未被访问过（即 visited[j] == 0），则递归调用 DFTraverse(j)，继续深度优先遍历邻接点j及其所有未被访问过的邻接点。

template
void ALGraph::DFTraverse(int v)
{
	EdgeNode* p = nullptr;
	cout << adjlist[v].vertex<<" ";
	visited[v] = 1;
	// 工作指针 p 指向顶点 v 的边表
	p = adjlist[v].firstEdge;
	// 依次搜索顶点 v 的邻接点 j 
	while (p != nullptr) {
		int j = p->adjvex;
		if (visited[j] == 0) {
			DFTraverse(j);
		}
		p = p->next;
	}
}

9.广度优先遍历。

工作原理：

1. 输出当前顶点:

   • 输出当前顶点v的值。

2. 标记当前顶点为已访问:

   • 将 visited[v] 设置为1，表示顶点v已被访问过。

3. 初始化队列:

   • 初始化队列Q，其中front和rear分别表示队列的头部和尾部。初始时，front和rear都设置为-1，表示队列为空。

4. 将当前顶点入队:

   • 将当前顶点v入队到队列Q中，同时更新队列尾部位置。

5. 遍历队列:

   • 当队列非空时，循环遍历队列中的每个顶点。在每次循环中，首先获取队头元素（即当前要处理的顶点）并输出其值。

6. 遍历当前顶点的邻接点:

   • 使用一个循环，遍历当前顶点v的所有邻接点。在每次循环中，保存当前结点 p 到 q，并将结点指针向前移动。
   • 对于每个邻接点j，如果邻接点j尚未被访问过（即 visited[j] == 0），则输出邻接点j的值，将其标记为已访问，并将其入队到队列Q中。

7. 结束条件:

   • 当队列为空时，表示所有可访问的顶点都已被处理完毕，遍历结束。

template
void ALGraph::BFTraverse(int v)
{
	// 采用顺序对列
	int w, j, Q[MaxSize];
	// 初始化队列
	int front = -1, rear = -1;
	EdgeNode* p = nullptr;
	cout << adjlist[v].vertex<<" ";
	visited[v] = 1;
	// 被访问顶点入队
	Q[++rear] = v;
	// 当对列非空时
	while (front != rear) {
		w = Q[++front];
		// 工作指针 p 指向顶点 v 的边表
		p = adjlist[w].firstEdge;
		while (p != nullptr) {
			j = p->adjvex;
			if (visited[j] == 0) {
				cout << adjlist[j].vertex<<" ";
				visited[j] = 1;
				Q[++rear] = j;
			}
			p = p->next;
		}
	}
}

10.拓扑排序。

工作原理：

1. 初始化:

   • 初始化一个计数器count为0，用于记录已经处理过的顶点数量。
   • 初始化一个顺序栈S，并设置栈顶指针top为-1，表示栈为空。
   • 遍历顶点表，将所有入度为0的顶点入栈。入度为0表示该顶点尚未被其他顶点所依赖。

2. 主循环:

   • 当栈不为空时，循环继续。
   • 从栈中取出一个入度为0的顶点j。
   • 输出顶点j的值，并将count加1。
   • 初始化工作指针p指向顶点j的边表。
   • 遍历顶点j的所有出边，将所有出边的邻接点的入度减1。
   • 如果邻接点的入度变为0，则将其入栈。
   • 继续处理下一个出边，直到遍历完所有出边。

3. 结束:

   • 如果处理过的顶点数量小于总顶点数，说明图中存在回路，输出“有回路”。否则，已经完成了拓扑排序。

template
void ALGraph::TopSort()
{
	// 累加器 count 初始化
	int i, j, k, count = 0;
	// 采用顺序栈并初始化
	int S[MaxSize], top = -1;
	EdgeNode* p = nullptr;
	// 扫描顶点表
	for (i = 0; i < vertexNum; i++) {
		if (adjlist[i].in == 0) {
			S[++top] = i;
		}
	}
	// 当栈中还有入度为0的顶点时
	while (top != -1) {
		// 从栈中取出入度为0的顶点
		j = S[top--];
		cout << adjlist[j].vertex;
		count++;
		// 工作指针p初始化
		p = adjlist[j].firstEdge;
		// 扫描顶点表，找出顶点j的所有出边
		while (p != nullptr) {
			k = p->adjvex;
			adjlist[k].in--;
			// 将入度为0的顶点入栈
			if (adjlist[k].in == 0) { 
				S[++top] = k;
			}
			p = p->next;
		}
	}	
	if (count < vertexNum) {
		cout << "有回路";
	}
}

11.主函数

int main()
{
	char ch[] = { 'A','B','C','D','E'};
	int i;
	// 建立
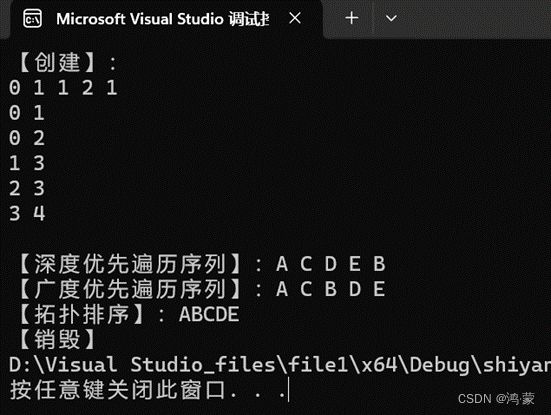
	cout << "【创建】：\n";
	ALGraph ALG{ch, 5, 5};  // 建立具有  个顶点  条边的有向图

	// 深度优先遍历
	for (i = 0; i < MaxSize; i++) {
		visited[i] = 0;
	}
	cout << "\n【深度优先遍历序列】：";
	ALG.DFTraverse(0);

	/*
	// 增加一个顶点
	cout << "\n【增加顶点】：E";
	ALG.AddVertex('E');

	// 增加一条弧
	cout << "\n【增加弧】：A->E";
	ALG.AddEdge(0, 4);

	// 删除一条弧
	cout << "\n【删除弧】：D->C";
	ALG.DeleteEdge(3, 2);

	// 深度优先遍历
	for (i = 0; i < MaxSize; i++) {
		visited[i] = 0;
	}
	cout << "\n【深度优先遍历序列】：";
	ALG.DFTraverse(0);
	*/

	// 广度优先遍历
	for (i = 0; i < MaxSize; i++) {
		visited[i] = 0;
	}
	cout << "\n【广度优先遍历序列】：";
	ALG.BFTraverse(0);

	// 拓扑排序
	for (i = 0; i < MaxSize; i++) {
		visited[i] = 0;
	}
	cout << "\n【拓扑排序】：";
	ALG.TopSort();

	// 销毁
	cout << "\n【销毁】";
	ALG.~ALGraph();

	return 0;
}

---

四、代码结构

---

五、测试结果

1.手绘邻接表

2.基本操作

---

        完整代码链接：https://download.csdn.net/download/weixin_73286497/88758698

        希望大家可以在该篇实验报告中有所收获，同时也感谢各位大佬的支持。文章如有任何问题请在评论区留言斧正，鸿蒙会尽快回复您的建议！