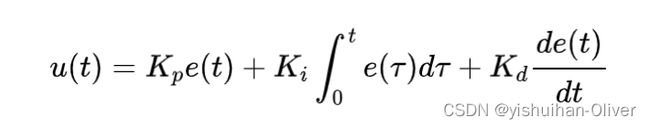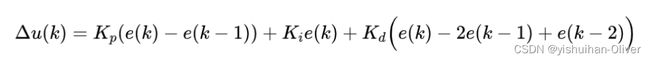位置式PID算法和增量式PID算法的差异

位置式PID算法和增量式PID算法的差异

==============以下内容来自​​​​​​​位置式PID算法和增量式PID算法的差异-电子发烧友网 (elecfans.com)==============

1、前言

控制系统通常根据有没有反馈会分为开环系统和闭环系统，在闭环系统的控制中，PID算法非常强大，其三个部分分别为；

• P：比例环节；
• I：积分环节；
• D：微分环节；

PID算法可以自动对控制系统进行准确且迅速的校正，因此被广泛地应用于工业控制系统。

2、开环控制

首先来看开环控制系统，如下图所示，隆哥蒙着眼，需要走到虚线旗帜所表示的目标位置，由于缺少反馈（眼睛可以感知当前距离和位置，由于眼睛被蒙上没有反馈，所以这也是一个开环系统），最终隆哥会较大概率偏离预期的目标，可能会运行到途中实线旗帜所表示的位置。

开环系统的整体结构如下所示：

这里做一个不是很恰当的比喻；

• Input：告诉隆哥目标距离的直线位置（10米）；
• Controller：隆哥大脑中计算出到达目标所需要走多少步；
• Process：双腿作为执行机构，输出了相应的步数，但是最终仍然偏离了目标；

看来没有反馈的存在，很难准确到达目标位置。

3、闭环控制

所以为了准确到达目标位置，这里就需要引入反馈，具体如下图所示：

在这里继续举个不怎么恰当的比喻；隆哥重获光明之后，基本可以看到目标位置了；

• 第一步Input：告诉隆哥目标距离的直线位置（10米）；
• 第二步Controller：隆哥大脑中计算出到达目标所需要走多少步；
• 第三步Process：双腿作为执行机构，输出了相应的步数，但是最终仍然偏离了目标；
• 第四步Feedback：通过视觉获取到目前已经前进的距离，（比如前进了2米，那么还有8米的偏差）；
• 第五步err：根据偏差重新计算所需要的步数，然后重复上述四个步骤，最终隆哥达到最终的目标位置。

4、PID

4.1 系统架构

虽然在反馈系统下，隆哥最终到达目标位置，但是现在又来了新的任务，就是又快又准地到达目标位置。所以这里隆哥开始采用PID Controller，只要适当调整P，I和D的参数，就可以到达目标位置，具体如下图所示：

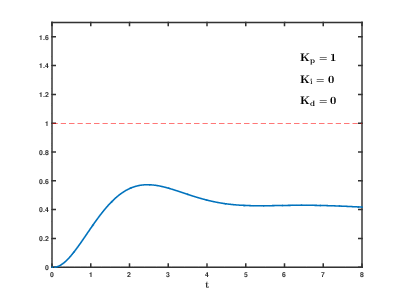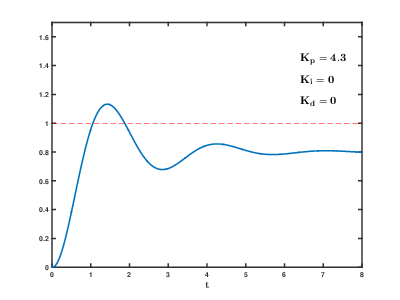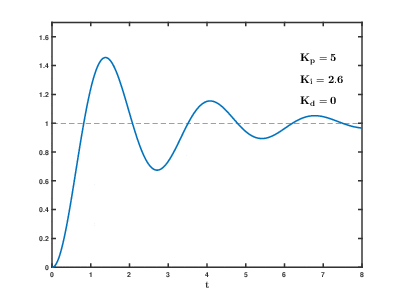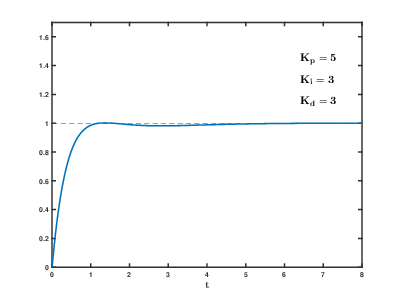
隆哥为了最短时间内到达目标位置，进行了不断的尝试，分别出现了以下几种情况；

• 跑得太快，最终导致冲过了目标位置还得往回跑；
• 跑得太慢，最终导致到达目标位置所用时间太长；

经过不断的尝试，终于找到了最佳的方式，其过程大概如下图所示：

这里依然举一个不是很恰当的比喻；

• 第一步：得到与目标位置的距离偏差（比如最开始是10米，后面会逐渐变小）；
• 第二步：根据误差，预估需要多少速度，如何估算呢，看下面几步；

P 比例则是给定一个速度的大致范围，满足下面这个公式：

因此比例作用相当于某一时刻的偏差（err）与比例系数的乘积，具体如下所示：

比例作用

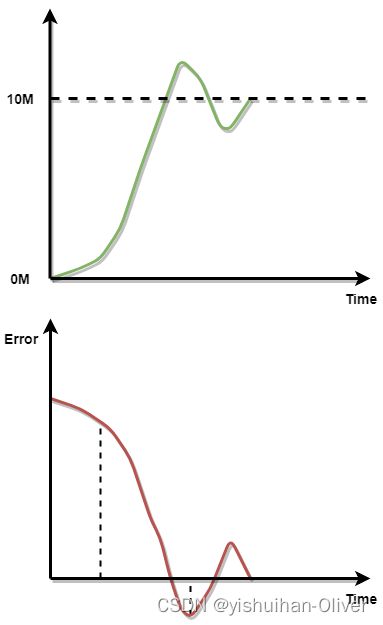
绿色线为上述例子中从初始位置到目标位置的距离变化； 红色线为上述例子中从初始位置到目标位置的偏差变化，两者为互补的关系；

---

I积分则是误差在一定时间内的和，满足以下公式：

如下图所示：

红色曲线阴影部分面积即为积分作用的结果，其不断累积的误差，最终乘以积分系数就得到了积分部分的输出；

---

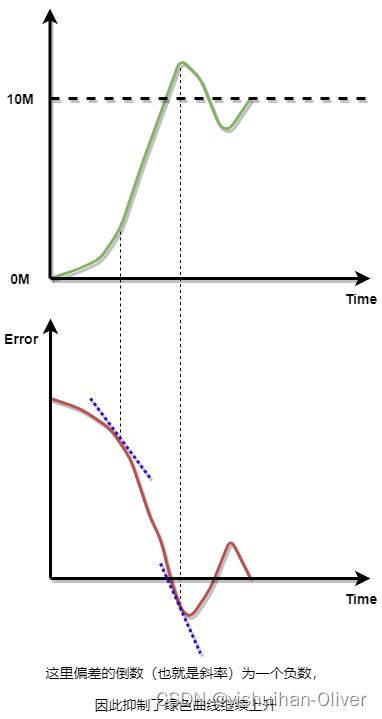
D微分则是误差变化曲线某处的导数，或者说是某一点的斜率，因此这里需要引入微分；

从图中可知，当偏差变化过快，微分环节会输出较大的负数，作为抑制输出继续上升，从而抑制过冲。

---

综上，分别增加其中一项参数会对系统造成的影响总结如下表所示：

参数	上升时间	超调量	响应时间	稳态误差	稳定性
Kp	减少	增加	小变化	减少	降级
Ki	减少	增加	增加	消除	降级
Kd	微小的变化	减少	减少	理论上没有影响	小，稳定性会提升

4.2 理论基础

上面扯了这么多，无非是为了初步理解PID在负反馈系统中的调节作用，下面开始推导一下算法实现的具体过程；PID控制器的系统框图如下所示：

因此不难得出输入和输出的关系：

Kp是比例增益；Ki是积分增益；Kd是微分增益；

4.3 离散化

在数字系统中进行PID算法控制，需要对上述算法进行离散化；假设系统采样时间为则将输入序列化得到：

将输出序列化得到：

• 比例项：离散化
• 积分项：
• 微分项：

所以最终可以得到式①，也就是网上所说的位置式PID：

将式①再做一下简化；

最终得到增量式PID的离散公式如下：

4.4 伪算法

这里简单总结一下增量式PID实现的伪算法：

previous_error:=0//上一次偏差 
integral:=0//积分和 
//循环 
//采样周期为dt 
loop: 
//setpoint设定值 
//measured_value反馈值 
error:=setpoint−measured_value//计算得到偏差 
integral:=integral+error×dt//计算得到积分累加和 
derivative:=(error−previous_error)/dt//计算得到微分 
output:=Kp×error+Ki×integral+Kd×derivative//计算得到PID输出 
previous_error:=error//保存当前偏差为下一次采样时所需要的历史偏差 
wait(dt)//等待下一次采用 
gotoloop

5、C++实现

这里是增量式PID算法的C语言实现；

/*******pid.cpp*******/
#ifndef _PID_SOURCE_
#define _PID_SOURCE_

#include 
#include 
#include "pid.h"

using namespace std;

class PIDImpl
{
    public:
        PIDImpl( double dt, double max, double min, double Kp, double Kd, double Ki );
        ~PIDImpl();
        double calculate( double setpoint, double pv );

    private:
        double _dt;
        double _max;
        double _min;
        double _Kp;
        double _Kd;
        double _Ki;
        double _pre_error;
        double _integral;
};


PID::PID( double dt, double max, double min, double Kp, double Kd, double Ki )
{
    pimpl = new PIDImpl(dt,max,min,Kp,Kd,Ki);
}
double PID::calculate( double setpoint, double pv )
{
    return pimpl->calculate(setpoint,pv);
}
PID::~PID() 
{
    delete pimpl;
}


/**
 * Implementation
 */
PIDImpl::PIDImpl( double dt, double max, double min, double Kp, double Kd, double Ki ) :
    _dt(dt),
    _max(max),
    _min(min),
    _Kp(Kp),
    _Kd(Kd),
    _Ki(Ki),
    _pre_error(0),
    _integral(0)
{
}

double PIDImpl::calculate( double setpoint, double pv )
{
    
    // Calculate error
    double error = setpoint - pv;

    // Proportional term
    double Pout = _Kp * error;

    // Integral term
    _integral += error * _dt;
    double Iout = _Ki * _integral;

    // Derivative term
    double derivative = (error - _pre_error) / _dt;
    double Dout = _Kd * derivative;

    // Calculate total output
    double output = Pout + Iout + Dout;

    // Restrict to max/min
    if( output > _max )
        output = _max;
    else if( output < _min )
        output = _min;

    // Save error to previous error
    _pre_error = error;

    return output;
}

PIDImpl::~PIDImpl()
{
}

#endif

/*********pid.h********/
#ifndef _PID_H_
#define _PID_H_

class PIDImpl;
class PID
{
    public:
        // Kp -  proportional gain
        // Ki -  Integral gain
        // Kd -  derivative gain
        // dt -  loop interval time
        // max - maximum value of manipulated variable
        // min - minimum value of manipulated variable
        PID( double dt, double max, double min, double Kp, double Kd, double Ki );

        // Returns the manipulated variable given a setpoint and current process value
        double calculate( double setpoint, double pv );
        ~PID();

    private:
        PIDImpl *pimpl;
};

#endif

/**********pid_example.cpp**********/

#include "pid.h"
#include 

int main() 
{

    PID pid = PID(0.1, 100, -100, 0.1, 0.01, 0.5);

    double val = 20;
    for (int i = 0; i < 100; i++) 
    {
        double inc = pid.calculate(0, val);
        printf("val:% 7.3f inc:% 7.3f\n", val, inc);
        val += inc;
    }

    return 0;
}

6、总结

以上内容总结了PID控制器算法在闭环系统中根据偏差变化的具体调节作用，每个环节可能对系统输出造成什么样的变化，给出了位置式和增量式离散PID算法的推导过程，并给出了位置式算法的C++程序实现。

============================================================

1、什么是增量式PID?

先看一下增量式PID的离散公式如下：

：比例系数 ：积分系数 ：微分系数 ：偏差

对于所谓的位置式，增量式的算法，这两者只是在算法的实现上的存在差异，本质的控制上对于系统控制的影响还是相同，单纯从输入和输出的角度来比较，具体如下表所示；

这里简单的说明一下；

• 位置式：位置式算法较为简单，直接输入当前的偏差 ，即可得到输出；
• 增量式：增量式算法需要保存历史偏差，，即在第次控制周期时，需要使用第和第次控制所输入的偏差，最终计算得到 ，此时，这还不是我们所需要的PID输出量；所以需要进行累加；

不难发现第一次控制周期时，即时；

由以上公式我们可以推导出下式：

所以可以看出，最终PID的输出量，满足以下公式：

可见增量式算法，就是所计算出的PID增量的历史累加和：

2、举个例子

2.1 位置式PID

下面从一个简单的例子中去理解一下增量式PID，这里依然举一个不是很恰当的例子；如果是位置式PID算法的话：

• 隆哥对一个直流电机进行调速，设定了转速为 1000；
• 这时由于反馈回来的速度和设定的速度偏差为 ；
• 经过位置式PID计算得到；
• 作为Process的输入值（可以是PWM的占空比），最终Process输出相应的PWM驱动直流电机；
• 反馈装置检测到电机转速，然后重复以上步骤；

整体框图如下所示：

2.2 增量式PID

对于增量式PID来说；

• 隆哥对一个直流电机进行调速，设定了转速为 1000；
• 这时由于反馈回来的速度和设定的速度偏差为 ，系统中保存上一次的偏差和上上次的偏差，这三个输入量经过增量PID计算得到；
• 系统中还保存了上一次的PID输出的，所以加上增量，就是本次控制周期的PID输出——；
• 作为Process的输入值（可以是PWM的占空比），最终Process输出相应的PWM驱动直流电机；
• 反馈装置检测到电机转速，然后重复以上步骤；

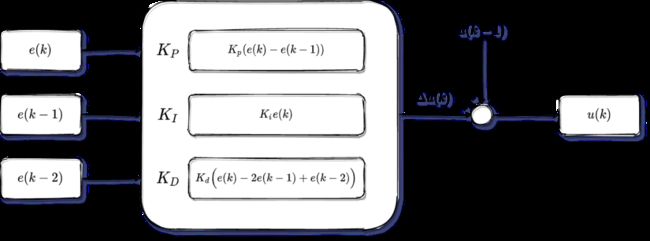
整体框图如下所示：

所以这里不难发现，所谓增量式PID，它的特点有：

• 需要输入历史的偏差值；
• 计算得到的是PID输出增量，因此每一次需要累加历史增量最为当前的PID输出；

下面简单介绍一下如何实现增量式PID算法；

3、伪算法

previous02_error:=0//上上次偏差
previous01_error:=0//上一次偏差
integral:=0//积分和
pid_out:=0//pid增量累加和
//循环
//采样周期为dt
loop:
//setpoint设定值
//measured_value反馈值
error:=setpoint−measured_value//计算得到偏差
proportion:=error-previous01_error//计算得到比例输出
integral:=error×dt//计算得到积分累加和
derivative:=(error−2*previous01_error+previous02_error)/dt//计算得到微分
pid_delta:=Kp×error+Ki×integral+Kd×derivative//计算得到PID增量
pid_out:=pid_out+pid_delta//计算得到PID输出

//保存当前的偏差和上一次偏差作为下一次采样所需要的历史偏差
previous02_error:=previous01_error
previous01_error:=error//保存当前偏差为下一次采样时所需要的历史偏差
wait(dt)//等待下一次采用
gotoloop

4、C语言实现

这里直接使用了TI公司的PID算法，做了积分抗饱和；具体可以参考controlSUITElibsapp_libsmotor_controlmath_blocksv4.2pid_grando.h

具体代码如下所示：

pid_grando.h

/*=================================================================================
Filename:PID_GRANDO.H
===================================================================================*/

#ifndef__PID_H__
#define__PID_H__

typedefstruct{_iqRef;//Input:referenceset-point
_iqFbk;//Input:feedback
_iqOut;//Output:controlleroutput
_iqc1;//Internal:derivativefiltercoefficient1
_iqc2;//Internal:derivativefiltercoefficient2
}PID_TERMINALS;
//note:c1&c2placedheretokeepstructuresizeunder8words

typedefstruct{_iqKr;//Parameter:referenceset-pointweighting
_iqKp;//Parameter:proportionalloopgain
_iqKi;//Parameter:integralgain
_iqKd;//Parameter:derivativegain
_iqKm;//Parameter:derivativeweighting
_iqUmax;//Parameter:uppersaturationlimit
_iqUmin;//Parameter:lowersaturationlimit
}PID_PARAMETERS;

typedefstruct{_iqup;//Data:proportionalterm
_iqui;//Data:integralterm
_iqud;//Data:derivativeterm
_iqv1;//Data:pre-saturatedcontrolleroutput
_iqi1;//Data:integratorstorage:ui(k-1)
_iqd1;//Data:differentiatorstorage:ud(k-1)
_iqd2;//Data:differentiatorstorage:d2(k-1)
_iqw1;//Data:saturationrecord:[u(k-1)-v(k-1)]
}PID_DATA;


typedefstruct{PID_TERMINALSterm;
PID_PARAMETERSparam;
PID_DATAdata;
}PID_CONTROLLER;

/*-----------------------------------------------------------------------------
DefaultinitalisationvaluesforthePIDobjects
-----------------------------------------------------------------------------*/

#definePID_TERM_DEFAULTS{
0,
0,
0,
0,
0
}

#definePID_PARAM_DEFAULTS{      
_IQ(1.0),
_IQ(1.0),
_IQ(0.0),
_IQ(0.0),
_IQ(1.0),
_IQ(1.0),
_IQ(-1.0)
}

#definePID_DATA_DEFAULTS{   
_IQ(0.0),
_IQ(0.0),
_IQ(0.0),
_IQ(0.0),
_IQ(0.0),
_IQ(0.0),
_IQ(0.0),
_IQ(1.0)
}


/*------------------------------------------------------------------------------
PIDMacroDefinition
------------------------------------------------------------------------------*/

#definePID_MACRO(v)      
      
/*proportionalterm*/   
v.data.up=_IQmpy(v.param.Kr,v.term.Ref)-v.term.Fbk;         
      
/*integralterm*/      
v.data.ui=_IQmpy(v.param.Ki,_IQmpy(v.data.w1, 
(v.term.Ref-v.term.Fbk)))+v.data.i1;      
v.data.i1=v.data.ui;    
      
/*derivativeterm*/    
v.data.d2=_IQmpy(v.param.Kd,_IQmpy(v.term.c1,
(_IQmpy(v.term.Ref,v.param.Km)-v.term.Fbk)))-v.data.d2;      
v.data.ud=v.data.d2+v.data.d1;          
v.data.d1=_IQmpy(v.data.ud,v.term.c2);     
      
/*controloutput*/     
v.data.v1=_IQmpy(v.param.Kp,
(v.data.up+v.data.ui+v.data.ud));
v.term.Out=_IQsat(v.data.v1,v.param.Umax,v.param.Umin);
v.data.w1=(v.term.Out==v.data.v1)?_IQ(1.0):_IQ(0.0);

#endif//__PID_H__

example

/*InstancethePIDmodule*/

PIDpid1={PID_TERM_DEFAULTS,PID_PARAM_DEFAULTS,PID_DATA_DEFAULTS};

main(){

pid1.param.Kp=_IQ(0.5);
pid1.param.Ki=_IQ(0.005);
pid1.param.Kd=_IQ(0);
pid1.param.Kr=_IQ(1.0);
pid1.param.Km=_IQ(1.0);
pid1.param.Umax=_IQ(1.0);
pid1.param.Umin=_IQ(-1.0);

}

voidinterruptperiodic_interrupt_isr(){

pid1.Ref=input1_1;//Pass_iqinputstopid1
pid1.Fbk=input1_2;//Pass_iqinputstopid1
PID_MACRO(pid1);//Callcomputemacroforpid1
output1=pid1.Out;//Accesstheoutputofpid1
}

5、总结

简单总结了位置式PID算法和增量式PID算法的差异，参考了TI公司的增量式PID算法实现，对于不同的控制对象可以根据系统要求选择合适的PID算法。

原文标题：干货 | 什么是PID算法，增量式PID又是什么?

文章出处：【微信公众号：电子工程世界】欢迎添加关注!文章转载请注明出处。

审核编辑：汤梓红

==============以上内容来自位置式PID算法和增量式PID算法的差异-电子发烧友网 (elecfans.com)==============

位置式PID与增量式PID区别浅析 (qq.com)