排序（5）——归并排序

六、归并排序

1.简介

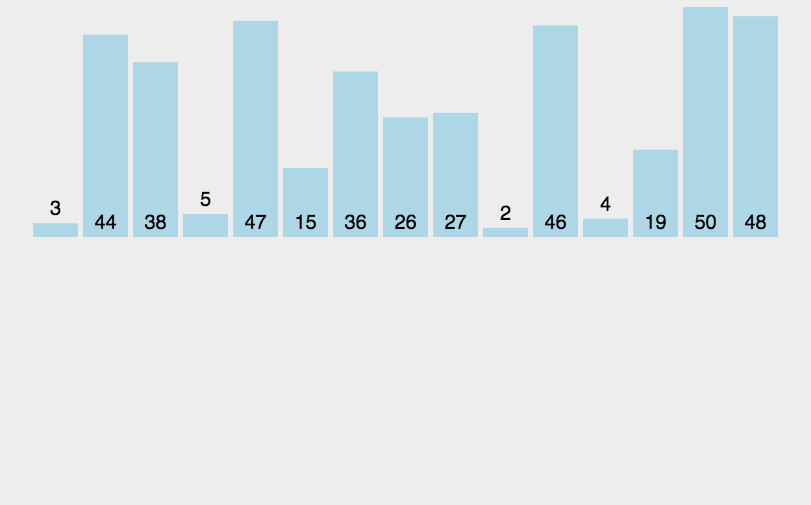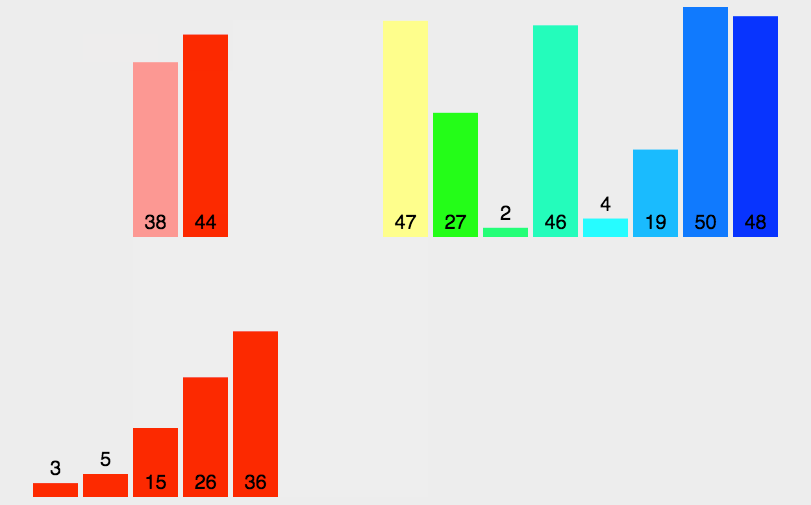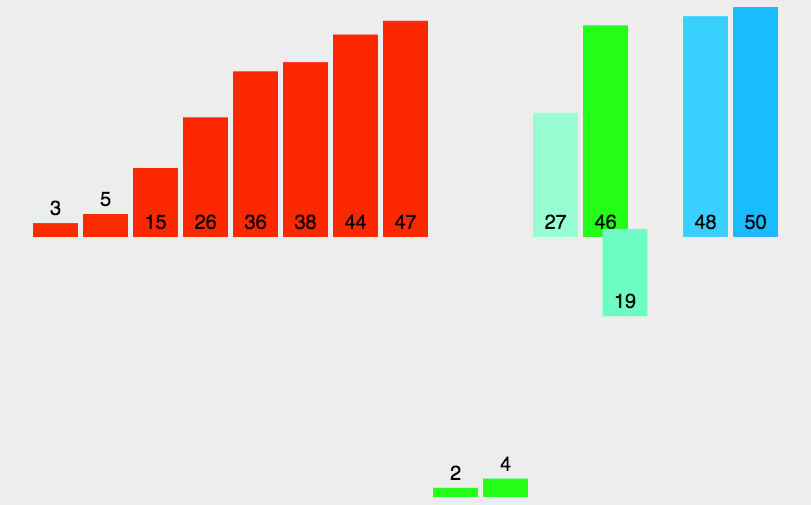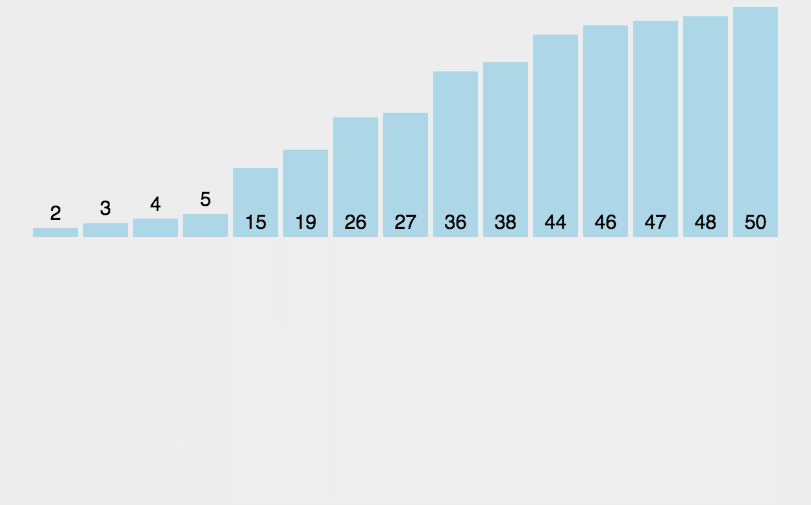
        归并排序也是一种很经典的排序算法，采用分治的思想方法进行数据的处理。归并讲究的是先拆后合，也就是分治中的分而治之。在拿到一组数据后，程序会将整个数据进行不断拆分直至有序，因为单个元素必然有序，所以归并排序最后拆分形成的组每组只有一个元素。对于这些已经有序的组别，再进行治，就是合并两个有序序列。如此采取先分再合的策略使得一组数据最后成为有序。

2.思路与代码

（1）归并排序---递归

         首先需要理解归并排序的工作流程。归并排序首先对元素进行分割，在不断的分割后形成了一批只有一个元素的组，这些组因为只有一个元素，所以可以被认为是有序的。在将所有元素都分割成为有序序列后，便可以放心地进行合并了。合并就是将两个有序数组合并为一个有序数组，通过合并操作，我们可以将这些有序序列不断合并最后完成整个数组的排序。

        

        接下来梳理一下归并排序的流程和一些要点，对于一个数组a：

        ①我们仔细观察会发现，所谓分割就是将数据的处理范围进行缩小，从最初的整个数组，每一次简化一半的规模直到规模为一个元素，此时相当于完成了分割。然后就是对这些小规模的数据组进行合并再合并完成排序。分割部分实际就是简单的收缩范围，并未对数据做出什么处理；合并部分则是有一种逆着分割的感觉，并对数据进行了关键的排序。如此可以发现，归并排序实际就是将数组不断分为左右两部分，再分割结束后再进行逐层处理，这就是我们之前所说过的后序遍历的情况。所以我们在递归实现归并排序的过程中可以参考后序遍历的模板。

        ②合并时是要完成排序操作的，所以对两个有序数组进行合并生成一个有序数组也是我们需要解决的问题。这个问题并不困难，只需要借助辅助空间，比较两个数组元素小的进入辅助数组即可。这也意味着我们需要额外的一个临时数组来帮助我们进行数组的合并操作。

        ③完成代码时，我们因为既需要递归，又需要开辟数组，所以最佳解决方案就是将二者分离为两个函数，这样就可因避免递归导致反复开空间，难以管理。

//归并排序
void _MergeSort(int* a, int* tmp, int begin, int end)
{
	if (begin >= end)
	{
		return;
	}

	int mid = (end + begin) / 2;

	_MergeSort(a, tmp, begin, mid);
	_MergeSort(a, tmp, mid + 1, end);

	int head1 = begin;
	int head2 = mid + 1;
	int cur = begin;
	while (head1 <= mid && head2 <= end)
	{
		if (a[head1] > a[head2])
		{
			tmp[cur++] = a[head2++];
		}
		else
		{
			tmp[cur++] = a[head1++];
		}
	}
	while (head1 <= mid)
	{
		tmp[cur++] = a[head1++];
	}
	while (head2 <= end)
	{
		tmp[cur++] = a[head2++];
	}
	for (int i = begin; i <= end; i++)
	{
		a[i] = tmp[i];
	}
}

void MergeSort(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		perror("malloc fail");
		return;
	}

	_MergeSort(a, tmp, 0, n - 1);

	free(tmp);
}

（2）归并排序---非递归

        在快速排序的递归改非递归时，我们指出递归变为非递归一般有两种途径：栈或者循环。像是快排一般的前序遍历使用栈是很顺手的，因为前序遍历先处理根结点，在根结点处理完后才在栈中存储接下来要处理的数据，这时根结点处理完成早已出栈，并无什么影响。但是归并排序属于后序遍历，相当于我们需要借助根结点得到接下来处理的数据，然后根结点不可以释放，因为最后仍需要处理根结点（合并）。相当于归并排序根结点需要二次使用，虽然我们可以使用两个栈，或者在入栈前先找到下一个区间再入栈等方法解决这个问题，但是嘛该用循环就要用，这里我们就用循环实现归并排序的非递归。

        因为归并排序的后序遍历注定了分割是“虚假的”，即我们可以主观认为数组中元素已经被分割好了。所以我们给出一个变量gap来标识合并过程下两个数组的规模。每一轮合并结束后gap就翻倍，这与递归下的逻辑相同。

        在具体的一轮排序中，需要很清晰两组数据的起始和终止位置。以变量i作为第一组数据的起始下标，因为一组数据规模是gap，所以第一组数据终止下标为i+gap-1。同理可以得到第二组数字的区间为[i+gap,i+2*gap-1]。当需要处理下一对时，给i加上2*gap即可。明确了这一点后，合并过程的排序逻辑就与递归无异了。

        最后需要注意的一点是不完全数组。当执行到一轮合并的最后一组数据时，因为我们的起始位置和终止位置都是根据i和gap计算所得的，所以需要判断并限制越界访问。当end1或begin2越界时，就说明不存在第二组数据，所以也就不需要进行合并操作了，直接终止循环即可；当只有end2越界时说明第二组数据和第一组数据规模不同，为了防止越界，只需要把第二组数据的终止下标end2人为改为整个数组最后一个元素下标就可以防止越界了。

void MergeSortNonR(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		perror("malloc fail");
		return;
	}

	int gap = 1;
	while (gap < n)
	{
		for (int i = 0; i < n; i += 2 * gap)
		{
			int begin1 = i, end1 = i + gap - 1;//归并中第一个区间的范围
			int begin2 = i + gap, end2 = i + 2 * gap - 1;//归并中第二个区间的范围
			int head1 = begin1, head2 = begin2;
			int cur = begin1;
			if (end1 >= n || begin2 >= n)//数据只存在于第一个区间中，而第二个区间没有数据，这时无需归并（因为只有一组数据已然有序）
			{
				break;
			}
			if (end2 >= n)//第二个区间数据不满，此时需要对第二个区间进行调整，然后再归并
			{
				end2 = n - 1;//这种情况只会在最后一组出现，所以直接赋值end2为序列最后一个元素下标即可
			}
			while (head1 <= end1 && head2 <= end2)
			{
				if (a[head1] < a[head2])
				{
					tmp[cur++] = a[head1++];
				}
				else
				{
					tmp[cur++] = a[head2++];
				}
			}
			while (head1 <= end1)
			{
				tmp[cur++] = a[head1++];
			}
			while (head2 <= end2)
			{
				tmp[cur++] = a[head2++];
			}
			for (int i = begin1; i <= end2; i++)
			{
				a[i] = tmp[i];
			}
		}
		gap *= 2;
	}
	free(tmp);
}

3.复杂度与稳定性分析

（1）时间复杂度

        因为归并排序和快速排序都是类似于二叉树的分治过程，所以归并排序的时间复杂度和快速排序的计算方法一样，每一层都是一次数组的遍历，不同的是快排层数在到之间不确定，而归并排序层数很明显是层。

        因此归并排序时间复杂度为。

（2）空间复杂度

        归并排序使用了一个临时数组作为辅助与拷贝，再加上递归开销，其空间开销为，根据大O渐进表示法，其空间复杂度为。

        我们所掌握的诸如快排、堆排序之类的排序算法一般称为内排序，因为他们都是在对内存中的数据进行排序。而归并排序虽然有O(n)的空间复杂度，但这也意味着归并排序可以应用于外排序，即对文件的数据排序中。在用归并排序进行外排序的时候，我们可以将一个新文件作为额外的空间使用，于是就可以在文件中排序了。

（3）稳定性

        归并排序是稳定的。

        归并排序对数据是整块整块处理的，可以说泾渭分明，相对位置维持的很好，所以是稳定的。