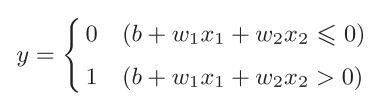《深度学习入门》学习笔记
原书:《深度学习入门:基于Python的理论与实现》
文章目录
- 前言
- 第一章 python入门
-
-
- 列表
- 字典
- 类
- numpy
- 广播
-
- 第二章 感知机
- 第三章 神经网络
-
-
- 激活函数
-
- 第四章 神经网络的学习
-
-
- 损失函数
- 求梯度
-
- 第五章 误差反向传播法
- 第六章 与学习相关的技巧
-
-
- 6.1 寻找最优参数
- 6.3 权重的初始值
- 6.4 正则化
- 6.4 超参数的验证
-
- 第七章 卷积神经网络
-
-
- 卷积
- 池化
- CNN的可视化
- 代表性的CNN
-
- 第八章 深度学习
-
-
- 提高识别精度
- VGG
- GoogLeNet
- ResNet
- 深度学习的高速化
-
前言
玩了一学期网络,发现自己只是个调包侠…老老实实学基础理论吧…
第一章 python入门
1.3
列表
a = [1, 2, 3, 4, 5] # 生成列表
a[0:2] # 获取索引为0到2(不包括2!)的元素
a[1:] # 获取从索引为1的元素到最后一个元素
a[:3] # 获取从第一个元素到索引为3(不包括3!)的元素
a[:-1] # 获取从第一个元素到最后一个元素的前一个元素之间的元素
a[:-2] # 获取从第一个元素到最后一个元素的前二个元素之间的元素
字典
me = {‘height’:180} # 生成字典
me[‘height’] # 访问元素
me[‘weight’] = 70 # 添加新元素
类
class Man:
def __init (self, name): # init左右两条下划 线
self.name = name
print(“Initialized!”)
def hello(self):
print("Hello " + self.name + “!”)
def goodbye(self):
print("Good-bye " + self.name + “!”)
m = Man(“David”)
m.hello()
m.goodbye()
构造函数(constructor)是进行初始化的方法,只在生成类的实例时被调用一次。
1.5
numpy
常用
A.dtype # 查看数据类型
X.flatten() # 将X转换为一维数组
X[np.array([0, 2, 4])] # 获取索引为0、2、4的元素
np.dot(A, B) #矩阵相乘
np.argmax(y) # 数组中最大值的索引
X > 15
array([ True, True, False, True, False, False], dtype=bool)
X[X>15]
array([51, 55, 19])
广播
第二章 感知机
第三章 神经网络
![]()
激活函数
sigmoid函数

ReLU函数
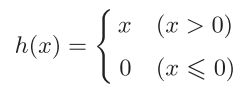
softmax函数(分类问题)

可能会溢出,超大值无法表示,改进:
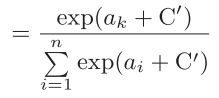
第四章 神经网络的学习
损失函数
均方误差

yk是表示神经网络的输出,tk表示监督数据,k表示数据的维数
交叉熵误差

由正确解标签所对应的输出结果决定
mini_batch学习时,求所有单个数据损失函数的总和,再取平均
求梯度
数值微分
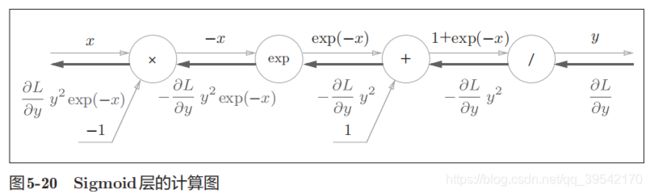
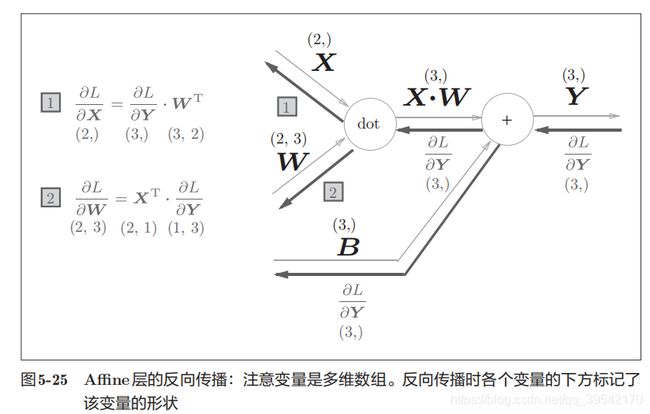
误差反向传播法
第五章 误差反向传播法
第六章 与学习相关的技巧
6.1 寻找最优参数
一般用SGD、Adam
SGD 随机梯度下降法(stochastic gradient descent)
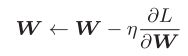
沿梯度方向更新参数,η表示学习率,实际上会取0.01或0.001这些事先决定好的值
Momentum
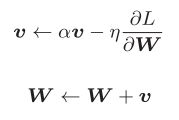
物体受梯度方向上的力和阻力,在这个力的作用下,物体的速度改变
α设定为0.9之类的值,对应物理上的地面摩擦或空气阻力。
AdaGrad
Ada来自英文单词Adaptive,即“适当的”的意思,会为参数的每个元素适当地调整学习率
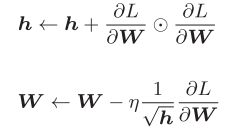
η表示学习率。
变量h保存了以前的所有梯度值的平方和
更新参数时可以调整学习的尺度。可以按参数的元素进行学习率衰减,使变动大的参数的学习率逐渐减小。
Adam
融合了Momentum和AdaGrad的方法
6.3 权重的初始值
Xavier、He(relu专用初始值)等初始值比较有效
不可以全部设0;在误差反向传播中,权重值会进行相同的更新,拥有对称的值,多个神经元失去了存在的意义
必须随机生成初始值,各层间传递的数据要有广度,激活函数的表现力不受限制
代码如下(示例):
6.4 正则化
过拟合的原因:
模型拥有大量参数,表现力强
训练数据少
抑制过拟合的方法
权值衰减
很多过拟合原本就是因为权重参数取值过大才发生的
以L2范数为例,它的权值衰减是1/2 λW2, 然后加到损失函数上。λ是控制正则化强度的超参数。λ设置得越大,对大的权重施加的惩罚就越重。
Dropout
学习的过程中随机删除神经元
6.4 超参数的验证
超参的范围要“大致”的指定,同时减少学习的epoch
以下为例:
以权值衰减系数为10−8到10−4、学习率为10−6到10−2的范围进行实验, 从这个结果可以看出,学习率在0.001到0.01、权值衰减系数在10−8到10−6之间时,学习可以顺利进行

第七章 卷积神经网络
术语:卷积(conv)、特征图(feature map)、填充(padding)、步幅(stride)
卷积
1、计算卷积输出大小
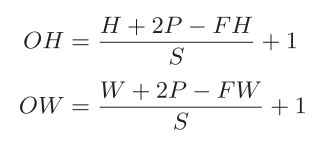
输出大小为(OH, OW),输入大小为(H, W),滤波器大小为(FH, FW),填充为P,步幅为S。
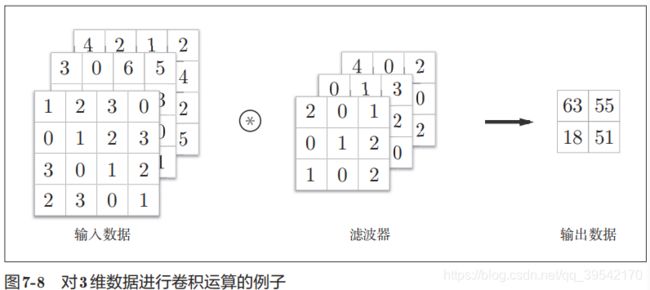
2、三维数据的卷积


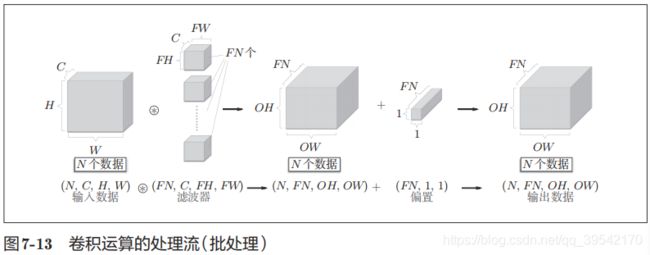
批处理
4维数据(batch_num, channel, height, width)
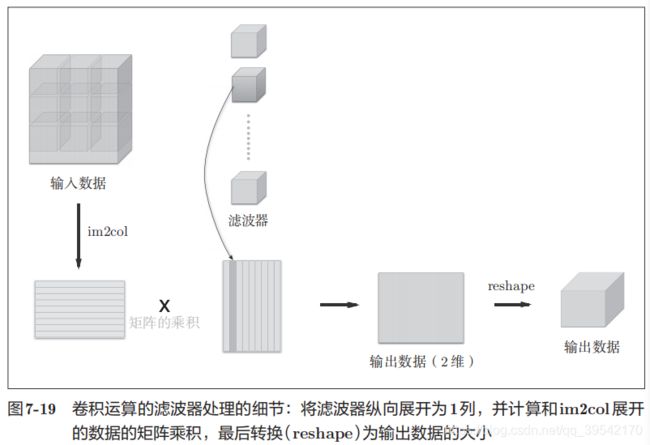
池化
CNN的可视化

右边的有规律的滤波器在观察边缘(颜色变化的分界线)和斑块(局部的块状区域)等

基于分层结构的信息提取
随着层次加深,神经元从简单的形状向“高级”信息变化
代表性的CNN
LeNet
AlexNet
第八章 深度学习
提高识别精度
集成学习
学习率衰减
Data Augmentation(数据扩充)
加深层(①减少网络参数数量 ②学习更加高效,各层要学习的问题分解成容易解决的简单问题 ) 从理论上无法解释怎样加深层
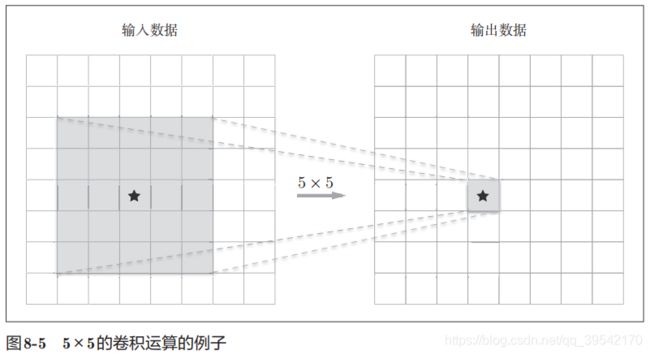
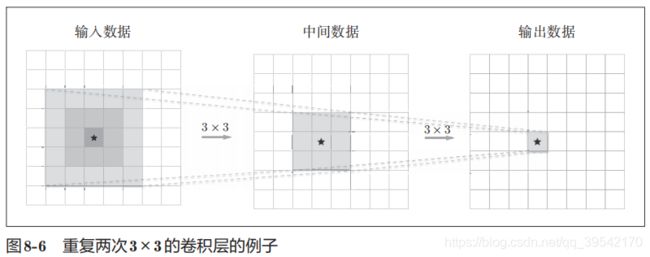
前者的参数数量25(5 × 5),后者一共是18(2 × 3 × 3)
叠加小型滤波器来加深网络还可以扩大感受野(receptive field,给神经元施加变化的某个局部空间区域)。
并且通过叠加层,将 ReLU等激活函数夹在卷积层的中间,进一步提高了网络的表现力。这是因为向网络添加了基于激活函数的“非线性”表现力,通过非线性函数的叠加,可以表现更加复杂的东西。
VGG
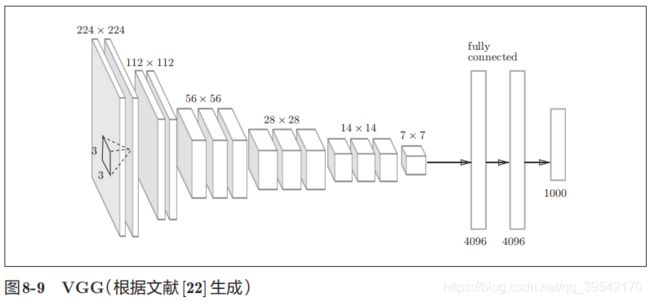
VGG是由卷积层和池化层构成的基础的CNN。
重复进行“卷积层重叠2次到4次,再通过池化层将大小减半”的处理,最后经由全连接层输出结果
GoogLeNet

GoogLeNet的特征是,网络不仅在纵向上有深度,在横向上也有深度(广度)。

Inception结构使用了多个大小不同的滤波器(和池化),最后再合并它们的结果。
此外,很多地方都使用了大小为1 × 1的滤波器的卷积层。这个1 × 1的卷积运算通过在通道方向上减小大小,有助于减少参数和实现高速化处理(???)
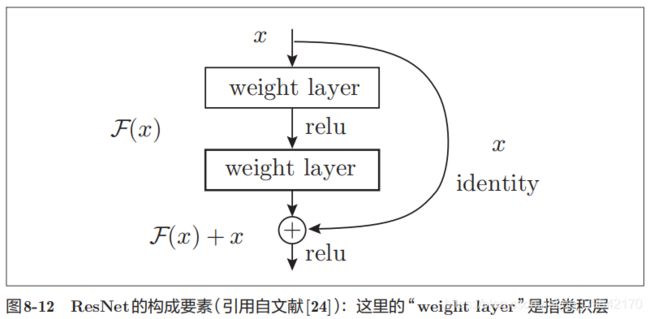
ResNet
它的特征在于具有比以前的网络更深的结构

通过快捷结构,原来的2层卷积层的输出F(x)变成了F(x) + x。反向传播时信号可以无衰减地传递,为加深层而导致的梯度变小的梯度消失问题就有望得到缓解。
深度学习的高速化
卷积层的处理时间加起来占GPU整体的95%,占CPU整体的89%!因此,如何高速、高效地进行卷积层中的乘积累加运算是深度学习的一大课题
① 基于GPU的高速化:
大型矩阵的乘积运算 ,这种大量的并行运算正是GPU所擅长的,CPU比较擅长连续的、复杂的计算)
提供GPU的公司主要有NVIDIA (英伟达)和 AMD。NVIDIA 提供了CUDA(面向GPU计算的综合开发环境),服务大多数深度学习框架
② 分布式学习
在多个GPU或者多台机器上进行分布式计算,
包含了机器间的通信、数据的同步等多个无法轻易解决的问题
支持分布式学习的框架有: Google的TensorFlow、微软的CNTK;
③ 运算精度的位数缩减
除了计算量之外,内存容量、总线带宽等也有可能成为瓶颈。所以要尽可能减少流经网络的数据的位数。
计算机中为了表示实数,主要使用64位或者32位的浮点数; 深度学习中使用16位的半精度浮点数(half float)
位数缩减是今后必须关注的一个课题,特别是在面向嵌入式应用程序中使用深度学习时