力扣● 435. 无重叠区间 ● 763.划分字母区间 ● 56. 合并区间 ●738. 单调递增的数字

● 435. 无重叠区间

跟弓箭题一样的原理：先集体对左边界排序，然后从第1个区间开始，当下一个区间的左边界比该区间的右边界要小的时候，就得去掉这个区间（count++），然后应该①直接更新该区间的右边界为和他重叠的所有区间的最小右边界（取这个和上一个的较小值，会使得更新的右边界越来越小，直到最小）。或者②维护一个right代表这个最小右边界，每一次统计之后更新这个right。

直接改：

class Solution {
public:
    static bool cmp(vector a,vector b){
        return a[0]>& intervals) {
        if(intervals.empty())return 0;
        sort(intervals.begin(),intervals.end(),cmp);    //左边界从小到大排
        int count=0;
        for(int i=1; i

使用变量right（注意下一个区间和这个不重叠的话要更新一下right为现在区间的右边界）：

class Solution {
public:
    static bool cmp(vector a,vector b){
        return a[0]>& intervals) {
        if(intervals.empty())return 0;
        sort(intervals.begin(),intervals.end(),cmp);    //左边界从小到大排
        int count=0,right=intervals[0][1];
        for(int i=1; i

● 763.划分字母区间

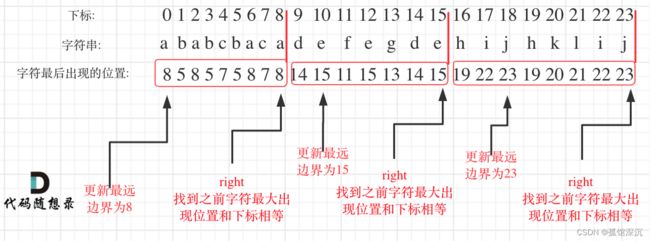
最主要的：每个节点的最远出现位置都要先求出来，挨个统计。

在遍历的过程中相当于是要找每一个字母的边界，如果找到之前遍历过的所有字母的最远边界，说明这个边界就是分割点了。此时前面出现过所有字母，最远也就到这个边界了。

可以分为如下两步：

• 统计每一个字符最后出现的位置
• 从头遍历字符，并更新字符的最远出现下标，如果找到字符最远出现位置下标和当前下标相等了，则找到了分割点

方案一：不用哈希映射（时间开销大）

class Solution {
public:
    vector partitionLabels(string s) {
        vector result;
        int right=INT_MIN,left=-1;//left是上一次的right，最远距离
        for(int i=0; i=0; --j){
                if(s[j]==s[i]){
                    break;          //j是s[i]最远的出现距离
                }
            }
            right=max(right,j);     //更新
            if(i==right){           //找到之前字符最大出现位置和下标相等
                result.push_back(right-left);
                left=right;
            }
        }
        return result;
        
    }
};

用哈希映射：

class Solution {
public:
    vector partitionLabels(string s) {
        vector result;
        map hash;
        for(int i=0; i

● 56. 合并区间

同样的，先对区间的左边界排序。这个题需要设置两个变量来保存重叠区间的最左边界（left）和最右边界（right），left和right分别初始化为第一个区间的左右边界，之后每遇到一个区间，如果这个区间左边界在right左边，意味着遇到了跟[left,right]重叠的区间，所以要更新right为最右边界，所以取max。否则的话跟之前的区间不重叠，那么可以把之前的[left,right]先保存到result，然后再更新left和right，意味着重新统计下一个重叠区间。

最后的[left,right]需要在循环外面保存。

class Solution {
public:
    static bool cmp(const vector & a,const vector & b){
        return a[0]> merge(vector>& intervals) {        
        vector> result;
        sort(intervals.begin(),intervals.end(),cmp);
        int left=intervals[0][0],right=intervals[0][1];
        for(int i=0; i{left,right});
                left=intervals[i][0];
                right=intervals[i][1];
            }
        }
        result.push_back(vector{left,right});
        return result;
    }
};

在代码随想录中，不维护两个自定义变量，而是维护result的最后一个区间，如果Intervals下一个区间跟result最后这个区间有重叠，我们应该更新result的最后这个区间（因为左边界排过序了所以只更新最右边界result.back()[1]）。否则作为一个新的统计重叠的区间加入到result。

class Solution {
public:
    static bool cmp(const vector & a,const vector & b){
        return a[0]> merge(vector>& intervals) {        
        vector> result;
        sort(intervals.begin(),intervals.end(),cmp);
        result.push_back(intervals[0]);
        for(int i=1; i

●738. 单调递增的数字

一对一对地改，比如32，先3减1，然后2变成9，所以结果是29。这是两位数的情况，那么两位数以上的呢，从左往右还是从右往左，例子：332，从左往右的话结果是329，错误，第一对33是符合的，处理第二对32的时候修改了之前符合条件的3，所以只能从右往左一对一对地改。遇到一对不符合非递减条件，就把前一个元素减减，然后当前元素及其之后的全部改成9（如果只把当前元素改9，不能保证非递减，结果也不一定是最大）。所以用flag记录要改成9的起点，初始化为size()，flag没有修改的话之后就没有元素会被修改成9。

这题细节方面：从变量flag到结尾全部设置为9；flag的初始值。

class Solution {
public:
    int monotoneIncreasingDigits(int n) {
        //后往前，一对一对地改
        string str=to_string(n);
        int flag=str.size();
        for(int i=str.size()-1; i>0; --i){
            if(str[i]

贪心一刷到此结束，根据代码随想录来总结一下：

局部最优推全局最优，for循环体里面处理局部的。严格证明不容易，想不到反例就是对的。对于贪心，我们不用一定要像数学证明题一样证明出来。