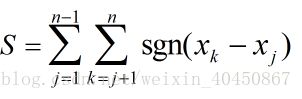Python的Mann-Kendall非参数检验和计算Hurst指数

 Mann-Kendall 检验法简称为 M-K 法， 是一种非参数统计检验方法， 可适用于不具有正态分布特征变量的趋势分析[38]。假定X1,X2,...Xn为时间序列变量[1]，n为时间序列的长度，M-K 法定义统计量S为

其中

 式中， xj、xk 分别为第j、k年对应的观测值，且j< k。

标准化的检验统计量Z为

 当n≥10时，统计量S近似服从正态分布，在不考虑序列中等值数据点的情况下，其均值E(S)=0 ​​​​​​​方差

                                                    D(S)=n(n-1)(2n+5)/18 。[2]

D(S)的计算论文中还有另外一种公式，D(S)和Var(S)均为S的方差。

g为将观测数据按照相同的元素进行分组，共有多少组g就是多少，tp为每一组元素个个数。

例如一组数据（1,1,2,2,2,4,4,4,4,4,7,7,7,8,9），其中可以分为（元素，个数）：（1,2个）（2:3个）（4，5个）（7,3个）（8,1个）（9,1个），则g为6，tp分别为2,3,5,3,1,1。依次带入再求和即可。当tp为1的时候tp-1为0，因此可以不考虑只出现一次的数，只考虑出现过多次的。如果一组数据每个数只出现过一次，那么求和部分的结果为0，方差只剩下n(n-1)(2n+5)/18。（参考文献[3]）

 

 Hurst指数根据R/S 分析求得，R/S 分析即重标极差分析，是一种基于长程相关思想的时间序列分析方法。这种方法由 H. E. Hurst 于1965年最先提出，后来伴随着非线性理论的发展而成长起来。R/S 分析具体过程参见地理数学方法[4]。

（1）计算S

import numpy as np
def s(inputdata):
#输入numpy数组
    n=inputdata.shape[0]
    t=0
    for i in np.arange(n):
        if i <=(n - 1):
            for j in np.arange(i+1,n):
                if inputdata[j]> inputdata[i]:
                    t=t+1
                elif inputdata[j]< inputdata[i]:
                    t=t-1
                else:
                    t=t
    return t

（2）计算Z

data=rd(r'D_S.tif')
#data为S，这里是针对一个单波段tif图像
n=10
var=n(n-1)(2n+5)/18
#n为时间序列的长度；var为方差
sv=np.sqrt(var)
#sv为标准差
r,c=data.shape
z=np.zeros(data.shape)
#由于时间久远，只用了for循环处理较慢，可用numpy矩阵运算效率更高
for i in range(r):
    for j in range(c):
        if data[i][j]>0:
            z[i][j]=(data[i][j]-1)/sv
        elif data[i][j]<0:
            z[i][j]=(data[i][j]+1)/sv

（3）计算beta

def beta(inputdata):
    n=inputdata.shape[0]
    t=[]
    for i in np.arange(n):
        if i <=(n - 1):
            for j in np.arange(i+1,n):
                t.append((inputdata[j]-inputdata[i])/((j-i)*1.0))
    return np.median(t)

（4）计算Hurst指数

import numpy as np
def Hurst(x):
    #x为numpy数组
    n=x.shape[0]
    t=np.zeros(n-1)      #t为时间序列的差分
    for i in range(n-1):
        t[i]=x[i+1]-x[i]
    mt=np.zeros(n-1)     #mt为均值序列,i为索引,i+1表示序列从1开始
    for i in range(n-1):
        mt[i]=np.sum(t[0:i+1])/(i+1)
    
    #Step3累积离差和极差,r为极差
    r=[]
    for i in np.arange(1,n):            #i为tao
        cha=[]
        for j in np.arange(1,i+1):
            if i==1:
                cha.append(t[j-1]-mt[i-1])
            if i>1:
                if j ==1:
                    cha.append(t[j-1]-mt[i-1])
                if j>1:
                    cha.append(cha[j-2]+t[j-1]-mt[i-1])    
        r.append(np.max(cha)-np.min(cha))
    s=[]
    for i in np.arange(1,n):
        ss=[]
        for j in np.arange(1,i+1):
            ss.append((t[j-1]-mt[i-1])**2)
        s.append(np.sqrt(np.sum(ss)/i))
    r=np.array(r)
    s=np.array(s)
    xdata=np.log(np.arange(2,n))
    ydata=np.log(r[1:]/s[1:])

    h,b= np.polyfit(xdata,ydata, 1)
    return h  

参考文献：

[1] 常远勇，侯西勇，毋亭，等．1998～2010年全球中低纬度降水时空特征分析［J］．水科学进展，2012，23（4）：475－484.

[2]  章诞武，丛振涛，倪广恒．基于中国气象资料的趋势检验方法对比分析［J］．水科学进展，2013，24（4）：490－496．

[3] https://www.researchgate.net/profile/Jyotsna_Singh15/post/Will_anyone_help_me_in_interpreting_the_result_of_mann-kendall_test_statistics_and_sens_slope_estimator2/attachment/59d6246279197b8077982b88/AS%3A312627941576704%401451547717495/download/Mann+Kendall+Analysis.pdf

[4] 陈彦光．地理数学方法：基础和应用［M］．北京：科学出版社，2011．