理解堆和二叉树
理解二叉树之前我们先来了解一下堆,了解堆有助于我们理解二叉树的结构。
堆
堆的概念
堆通常是一个可以被看做一棵树的数组对象,因此常常是通过数组的形式来实现的。
堆的条件
堆有两个条件:
1.是完全二叉树
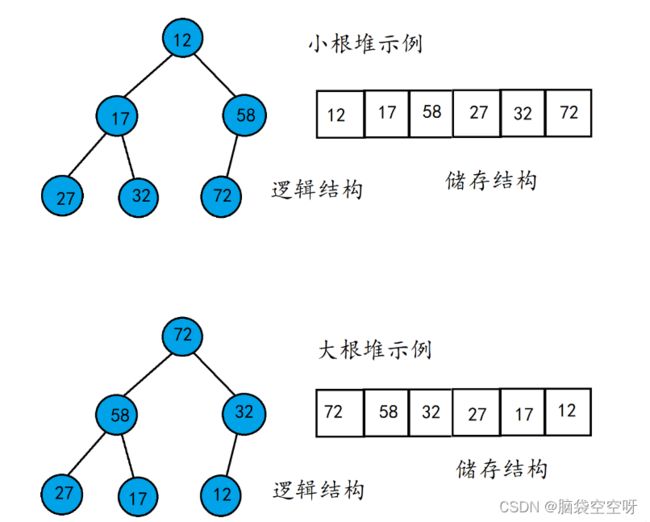
2.堆分为大(根)堆和小(根)堆:满足任意结点的值都大于其子树中结点的值,叫做大堆;反之就是小堆。
堆的结构
堆是一种完全二叉树,物理结构上是一段连续的数组区间,逻辑结构上是一颗完全二叉树。
堆的应用
1.堆排序O(NlogN)
2.topk-优质筛选问题
3.优先级队列
我们先定义一个堆结构,堆的物理结构是一段连续的数组区间,所以我们定义堆跟顺序表一样就可以。
typedef int HPDataType;
typedef struct Heap {
HPDataType* a;
int size;
int capacity;
}HP;
向上调整
向上调整的规则是调整之前这个堆必须是小/大堆。
void Swap(HPDataType* p1, HPDataType* p2) {
HPDataType tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}
Swap函数用来交换两个HPDataType类型的指针。
void AdjustUp(HPDataType* a, int child) {
int parent = (child - 1) / 2;
while (child > 0) {
if (a[child] < a[parent]) {
Swap(&a[child], &a[parent]);
child = parent;
parent = (child - 1) / 2; //孩子下标找父亲:parent=(child-1)/2
}
else {
break;
}
}
}
AdjustUp函数用来实现小堆的插入,我们定义了parent是新插入的child的父节点,如果插入的child比parent大,那么就交换,然后再判断交换之后的数跟新的父节点的大小重复之前的操作,直到根节点比较完为止,这样最小的数就在根节点的位置。
for (int i = 1; i < n; i++) {
AdjustUp(a,i);
}
向上调整建堆需要插入之前就是一个堆,所以我们把第一个数当作一个堆,从第2个数开始插入即可,这样小堆就建好了。
向下调整
向下调整的规则是调整之前这个堆的子树(除了根节点)必须是小/大堆。代码如下:
void AdjustDown(int *a,int n,int parent){
int child = parent * 2 + 1;
while (child
if (child+1
++child;
}
if (a[child] < a[parent]) {//小堆< 大堆>
Swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else {
break;
}
}
}
我们定义一个child来求parent的子节点,这里我们建小堆就选出child兄弟节点中小的那个,如果child的值小于节点的值就交换,直到比较完所有子树,这样最小的数就在根节点的位置。
堆排序
for (int i = (n-1-1)/2; i >=0; i--) {
AdjustDown(a, n, i);
}
从最后一个非叶子结点的双亲开始,最后一个结点的下标是: n- 1,它的双亲是: ((n - 1) - 1) / 2,根头节点比较,选出最小的,首尾交换,最小的放到最后的位置,把最后一个数据,不看做堆里面的,向下调整就可以选出次小的,依次重复就得到一个降序数组。也可以写成下面代码:
int end = n - 1;
while (end>0) {
Swap(&a[0], &a[end]);
//再调整,选出次小的数(上面最后一个数的下标就是下面的数据个数)
AdjustDown(a, end, 0);
--end;
}
我们可以得到一个结论:升序-建大堆、降序-建小堆。
二叉树
一棵二叉树是结点的一个有限集合,该集合: 1. 或者为空 2. 由一个根节点加上两棵别称为左子树和右子树的二叉树组成。
从上图可以看出: 1. 二叉树不存在度大于2的节点 2. 二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树。
有两种特殊的二叉树:满二叉树和完全二叉树。
1. 满二叉树:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。
2. 完全二叉树:前k-1层是满二叉树,第k层从左边开始节点必须相邻中间不能间隔开。满二叉树是一种特殊的完全二叉树。
我们定义一个二叉树结构,里面包含父节点,左孩子和右孩子。
typedef int BTDataType;
typedef struct BinaryTreeNode
{
BTDataType data;
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
}BTNode;
节点初始化
我们用BuyNode函数来进行初始化节点。
BTNode* BuyNode(BTDataType x) {
BTNode* node = (BTNode*)malloc(sizeof(BTNode));
if (node == NULL) {
perror("malloc fail");
return NULL;
}
node->data = x;
node->left = NULL;
node->right = NULL;
return node;
}
销毁二叉树
我们定义一个BTreeDestroy来进行二叉树的销毁。
void BTreeDestroy(BTNode* root);
代码实现:
void BTreeDestroy(BTNode* root) {
if (root == NULL)
return;
BTreeDestroy(root->left);
BTreeDestroy(root->right);
free(root);
}
如果节点为空直接返回,不为空就依次遍历左右孩子直到节点为空返回,最后释放节点。
前序遍历
我们定义一个PrevOrder来进行前序遍历。
void PrevOrder(BTNode* root);
函数实现:
void PrevOrder(BTNode* root) {
if (root == NULL) {
printf("NULL ");
return;
}
printf("%d ", root->data);
PrevOrder(root->left);
PrevOrder(root->right);
}
如果是空节点就直接返回,前序遍历的规则是(根->左节点->右节点),因为要一直遍历直到遍历完整个二叉树所以我们可以用递归来实现,递归终止条件就是root==NULL。
中序遍历
我们定义一个InOrder来进行中序遍历。
void InOrder(BTNode* root);
函数实现:
void InOrder(BTNode* root) {
if (root == NULL) {
printf("NULL ");
return;
}
InOrder(root->left);
printf("%d ", root->data);
InOrder(root->right);
}
中序遍历的规则是(左节点->根->右节点),其他的操作跟之前一样。
后序遍历
我们定义一个NextOrder来进行后序遍历。
void NextOrder(BTNode* root);
函数实现:
void NextOrder(BTNode* root) {
if (root == NULL) {
printf("NULL ");
return;
}
NextOrder(root->left);
NextOrder(root->right);
printf("%d ", root->data);
}
后序遍历的规则是(左节点->右节点->根),其他的操作跟之前一样。
层序遍历
我们定义一个LevelOrder来进行后序遍历。
代码实现:
void LevelOrder(BTNode* root) {
Queue q;
QueueInit(&q);
if (root)
QueuePush(&q, root);
while (!QueueEmpty(&q)) {
BTNode* front = QueueFront(&q);
QueuePop(&q);
printf("%d ", front->data);
if (front->left)
QueuePush(&q, front->left);
if (front->right)
QueuePush(&q, front->right);
}
printf("\n");
QueueDestroy(&q);
}
层序遍历的核心思想是:父节点出队列则带两个子节点进队列。所以想要层序遍历就需要用到队列,忘记队列是什么样的可以回顾我上一篇博客。
我们先进行队列的初始化,如果节点不为空就插入到队列中,当队列不为空时我们定义一个front指针来记录访问到的头节点然后把头节点删除再打印front指针记录的值,头节点出队列后我们让头节点的左右孩子进队列中依次循环即可,遍历完所有节点再销毁二叉树。
节点个数
我们定义一个BTreeSize来求二叉树节点的个数。
void BTreeSize(BTNode* root);
代码实现:
int size = 0;
void BTreeSize(BTNode* root) {
if (root == NULL) {
return;
}
++size;
BTreeSize(root->left);
BTreeSize(root->right);
}
遍历整个二叉树,如果根节点为空直接返回,不为空就++size,然后依次遍历左右子树。
我们也可以将上面代码进行优化:
return root == NULL ? 0 : BTreeSize(root->left) + BTreeSize(root->right) + 1;
如果节点为空就返回0,结点不为空就继续遍历左右孩子,直到左右孩子为空进行+1然后返回上一层再+1依次迭代就可以求出二叉树节点个数。
二叉树高度
我们定义一个BTreeHeight函数来求二叉树的高度。
int BTreeHeight(BTNode* root);
函数实现:
int BTreeHeight(BTNode* root) {
if (root == NULL) {
return 0;
}
int leftHeight = BTreeHeight(root->left);
int rightHeight = BTreeHeight(root->right);
return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}
判断二叉树的高度就是判断左右子树中哪个最高,所以我们定义了leftHeight和rightHeight分别记录左右子树的高度,如果左子树的高度大于右子树就返回,反之则返回右子树。
第k层结点个数
我们定义一个BTreeLeveKSize函数来求二叉树第k层节点的个数。
int BTreeLeveKSize(BTNode* root, int k);
代码实现:
int BTreeLeveKSize(BTNode* root, int k) {
assert(k > 0);
if (root == NULL) {
return 0;
}
if (k == 1) {
return 1;
}
return BTreeLeveKSize(root->left, k - 1) + BTreeLeveKSize(root->right, k - 1);
}
找第k层节点的个数我们必须保证k>0,如果是空树直接返回0,如果不是空树我们就需要在左右子树中找第k层节点的个数然后相加,每次往下一层寻找就需要k-1,直到k==1就找到了然后相加。
查找值为x的节点
我们定义一个BTreeFind函数来查找二叉树中值为x的节点。
BTNode* BTreeFind(BTNode* root, BTDataType x);
代码实现:
BTNode* BTreeFind(BTNode* root, BTDataType x) {
if (root == NULL) {
return NULL;
}
if (root->data == x) {
return root;
}
BTNode* ret1 = BTreeFind(root->left, x);
if (ret1) {
return ret1;
}
BTNode* ret2 = BTreeFind(root->right, x);
if (ret2) {
return ret2;
}
return NULL;
}
如果是空树就直接返回空,如果节点的值是x就直接返回,不是的话我们定义ret1和ret2分别用来记录寻找的在左子树和右子树中x的值然后返回,如果没找到就返回空。
判断是否是完全二叉树
我们定义一个BinaryTreeComplete函数来判断二叉树是不是完全二叉树。
代码实现:
bool BinaryTreeComplete(BTNode* root) {
Queue q;
QueueInit(&q);
if (root)
QueuePush(&q, root);
while (!QueueEmpty(&q)) {
BTNode* front = QueueFront(&q);
QueuePop(&q);
//遇到空就跳出
if (front == NULL)
break;
QueuePush(&q, front->left);
QueuePush(&q, front->right);
}
//检查后面的节点有没有非空
//有非空,不是二叉树
while (!QueueEmpty(&q)) {
BTNode* front = QueueFront(&q);
QueuePop(&q);
if (front) {
QueueDestroy(&q);
return false;
}
}
QueueDestroy(&q);
return true;
}
判断是不是完全二叉树就需要判断每一层节点之间是不是空,因此需要用到队列来进行层序遍历。如果遇到空就跳出,然后检查后面的节点有没有非空。如果有非空,就不是二叉树;反之就返回true。注意:空树是满二叉树也是完全二叉树,所以可以直接返回true。
如果觉得这篇文章对你有帮助可以收藏下来,也欢迎大家进行批评指正,理解堆和二叉树可以帮助我们更好的编写程序,一起加油![]()
![]()
![]()