贪心算法详解
目录
用贪心法求解的问题应具有的性质:
1.贪心选择性质:
2、最优子结构性质:
3、贪心法的一般求解过程
问题一:求解畜栏保留问题。
思路:
代码:
运行截图:
问题二:求解区间相交问题。
思路:
代码:
测试截图:
问题三:哈夫曼树
构造哈夫曼树:
代码:
运行截图:
哈夫曼树加密:
思路:
代码:
运行截图:
用贪心法求解的问题应具有的性质:
贪心法总是做出在当前看来最好的选择,这个局部最优选择仅依赖以前的决策,不依赖于以后的决策。由于贪心法一般不会测试所有可能路径,而且容易过早做决定,因此有些问题可能不会找到最优解,能够采用贪心法求解的问题一般具有两个性质——贪心选择性质和最优子结构性质,所以贪心算法一般需要证明满足这两个性质。
1.贪心选择性质:
所谓贪心选择性质是指所求问题的整体最优解可以通过一系列局部最优的选择(即贪心选择)来达到。也就是说,贪心法仅在当前状态下做出最好选择,即局部最优选择,然后再去求解做出这个选择后产生的相应子问题的解。它是贪心法可行的第一个基本要素,也是贪心算法与后面介绍的动态规划算法的主要区别。
对于一个具体问题,要确定它是否具有贪心选择性质,必须证明每一步所做的贪心选择最终导致问题的整体最优解。这通常采用数学归纳法来证明,先考虑问题的一个整体最优解﹐并证明可以修改这个最优解,使其从贪心选择开始,在做出贪心选择后原问题转化为规模较小的类似问题,通过每一步的贪心选择,最后可得到问题的整体最优解。
2、最优子结构性质:
如果一个问题的最优解包含其子问题的最优解,则称此问题具有最优子结构性质。问题的最优子结构性质是该问题可用动态规划算法或贪心法求解的关键特征。
在证明问题是否具有最优子结构性质时通常采用反证法来证明,先假设由问题的最优解导出的子问题的解不是最优的,然后证明在这个假设下可以构造出比原问题的最优解更好的解,从而导致矛盾。
3、贪心法的一般求解过程
用贪心法求解问题的基本思路如下:
(1) 建立数学模型来描述问题。
(2)把求解的问题分成若干个子问题。
(3) 对每一个子问题求解,得到子问题的局部最优解。
(4)把子问题的局部最优解合成原来解问题的一个解。
问题一:求解畜栏保留问题。
农场有n头牛,每头牛会有一个特定的时间区间[b,e]在畜栏里挤牛奶,并且一个畜栏里在任何时刻只能有一头牛挤奶。现在农场主希望知道最少畜栏能够满足上述要求,并给出每头牛被安排的方案。对于多种可行方案,输出一种即可。(注[2,4] 与 [4,7]是交叉的,是不兼容活动)
思路:
采用与求解活动安排问题类似的贪心思路将所有活动这样排序: 结束时间相同按开始时间递增排序,否则按结束时间递增排序。求出一个最大兼容活动子集,将它们安排在一个畜栏中(畜栏编号为1);如果没有安排完,在剩余的活动中求下一个最大兼容活动子集,将它们安排在另一个畜栏中(畜栏编号为2),依此类推。也就是说,最大兼容活动子集的个数就是最少畜栏个数。
代码:
#include
#include
#include
using namespace std;
#define MAX 51
//问题表示
struct Cow //奶牛的类型声明
{ int no; //牛编号
int b; //起始时间
int e; //结束时间
bool operator<(const Cow &s) const //重载<关系函数
{ if (e==s.e) //结束时间相同按开始时间递增排序
return b<=s.b;
else //否则按结束时间递增排序
return e<=s.e;
}
};
int n=5;
Cow A[]={{0},{1,1,10},{2,2,4},{3,3,6},{4,5,8},{5,4,7}}; //下标0不用
//求解结果表示
int ans[MAX]; //ans[i]表示第A[i].no头牛的蓄栏编号
void solve() //求解最大兼容活动子集
{ sort(A+1,A+n+1); //A[1..n]按指定方式排序
memset(ans,0,sizeof(ans)); //初始化为0
int num=1; //蓄栏编号
for (int i=1;i<=n;i++) //i、j均为排序后的下标
{ if (ans[i]==0) //第i头牛还没有安排蓄栏
{ ans[i]=num; //第i头牛安排蓄栏num
int preend=A[i].e; //前一个兼容活动的结束时间
for (int j=i+1;j<=n;j++) //查找一个最大兼容活动子集
{ if (A[j].b>preend && ans[j]==0)
{ ans[j]=num; //将兼容活动子集中活动安排在num蓄栏中
preend=A[j].e; //更新结束时间
}
}
num++; //查找下一个最大兼容活动子集,num增1
}
}
}
int main()
{ solve();
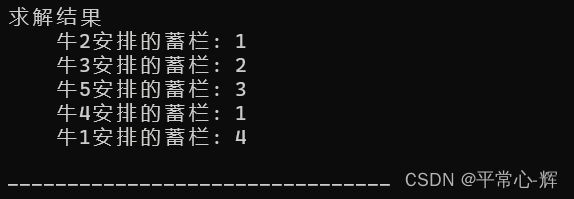
printf("求解结果\n");
for (int i=1;i<=n;i++){
printf(" 牛%d安排的蓄栏: %d\n",A[i].no,ans[i]);
}
return 0;
} 运行截图:
问题二:求解区间相交问题。
给定α轴上的n 个闭区间,去掉尽可能少的闭区间,使剩下的闭区间都不相交。对于给定的n个闭区间,计算去掉的最少闭区间数。
输入描述:对于每组输入数据,输入数据的第1行是正整数n(l≤n≤40 000),表示闭区间数;在接下来的n行中,每行有两个整数,分别表示闭区间的两个端点。
思路:
1、先将输入的区间进行处理,让区间中的元素,数字小的在前面,数字较大的在后面。例如[5,2],调整为[2,5]。
2、按照区间尾部从小到大进行排序。
3、记录区间尾部的数值为preend,如果下一个区间的头部数值大于preend,ans加一,更新preend为当前区间的尾部数值。重复上述过程,最终结果为区间的数量减去ans(n-ans)。
代码:
#include
#include
using namespace std;
#define MAX 40001
//问题表示
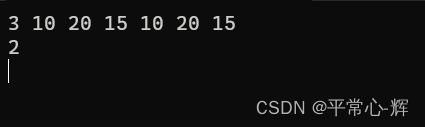
//输入测试数据 3 10 20 15 10 20 15
int n;
struct NodeType
{ int b; //区间首部
int e; //区间尾部
bool operator<(const NodeType &s) const
{ if (e==s.e)
return bA[i].e) //交换首尾部,使首部小于尾部
{ t=A[i].b;
A[i].b=A[i].e;
A[i].e=t;
}
sort(A,A+n); //排序
int preend=A[0].e;
ans=1;
for(i=1; ipreend) //A[j]与前一个求解不相交
{ ans++;
preend=A[i].e;
}
}
ans=n-ans;
}
int main()
{ while(scanf("%d",&n)!=EOF) //尽管题目中只有一个测试用例,但实际可以有多个
{ for(int i=0; i 测试截图:
问题三:哈夫曼树
给定N个权值作为N个叶子结点,构造一棵二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树,权值较大的结点离根较近。
构造哈夫曼树:
1)由给定的n个权值{w1, w2 , … , wn}构造n棵只有一个叶子结点的二叉树,从而得到一个二叉树的集合F={T1,T2,…,Tn}。
(2)在F中选取根结点的权值最小和次小的两棵二叉树作为左,右子树构造一棵新的二叉树,这棵新的二叉树的根结点的权值为其左、右子树根结点的权值之和,即合并两棵二叉树为一棵二叉树。
(3)重复步骤(2),当F中只剩下一棵二叉树时,这棵二叉树便是所要建立的哈夫曼树。
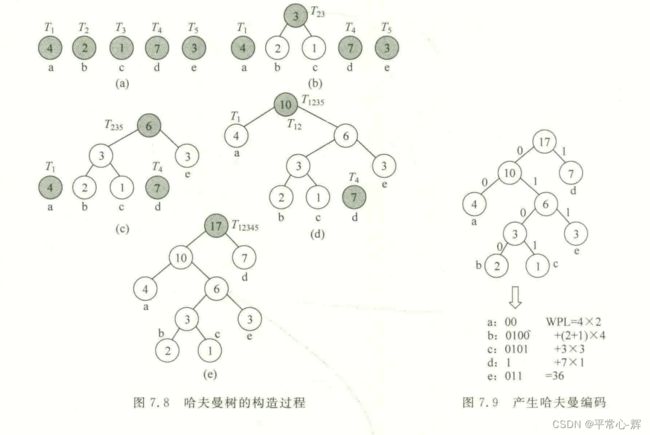
例如:给定a~e 5个字符,它们的权值集合为W={4,2,1,7,3},构造哈夫曼树的过程如下图所示。
在哈夫曼树的构造过程中,每次都合并两棵根结点权值最小的二叉树,这体现出贪心法的思想。那么是否可以像前面介绍的算法一样,先按权值递增排序,然后依次构造哈夫曼树呢?由于每次合并两棵二叉树时都要找最小和次小的根结点,而且新构造的二叉树也参加这一过程,如果每次都排序,这样花费的时间更多,所以一般不这样做,而是在已构造的二叉树中直接通过比较来找最小和次小的根结点。
由n个权值构造的哈夫曼树的总结点个数为2n一1,每个结点的二进制编码长度不会超过树高,可以推出这样的哈夫曼树的高度最多为n。所以用一个数组ht[0...2n—2]存放哈夫曼树,其中 ht[0...n一1]存放叶子结点, ht[n..n一2]存放其他需要构造的结点, ht[i.parent]为该结点的双亲在ht数组中的下标, ht[i]. parent= -1 表示它为根结点,.ht[i].lchild,ht[i].rchild分别为该结点的左、右孩子的下标。
用map
由于需要多次选择两棵根结点最小和次小的子树合并,为此设计一个小根堆来查找这样的子树。
代码:
#pragma warning(disable:4786)
#include
#include
#include
#include
#include 运行截图:
哈夫曼树加密:
有一个英文句子str="The following code computes the intersection of two arrays”其中各个字符出现的次数,以其为频度构造对应的哈夫曼编码,将该英文句子进行编码得到enstr,然后将enstr解码为destr。编写程序实现上述功能。
思路:
首先统计str 中各个字符出现的次数,用map
代码:
#pragma warning(disable:4786)
#include
#include
#include
#include
#include 运行截图:
如果本文中存在不正确的地方,恳请道友批评指正。