数据结构与算法——二分查找

二分思想

• 数据结构必须先排好序，可以在数据规模的对数时间复杂度内完成查找
• 二分查找要求线性表具有有随机访问的特点（例如数组），也要求线性表能够根据中间元素的特点推测它两侧元素的性质。

二分查找针对的是一个有序的数据集合，查找思想有点类似分治思想。每次都通过跟区间的中间元素对比，将待查找的区间缩小为之前的一半，直到找到要查找的元素，或者区间被缩小为 0。

间复杂度分析

处理的元素个数为$n$
第1次循环所要处理的元素是$n$
第2次循环所要处理的元素是$\frac{1}{2}n$
$\cdots$
第$k$次循环所要处理的元素是$\frac{1}{2^k}n$
循环停止的条件为$$\frac{1}{2^k}n=1$$
因为$\frac{1}{2^k}n\ge 1$，取整后当为1时停止循环
解得上式$k={\log }_{2}n$
所以时间复杂度为$O({\log }_{2}n)$

二分查找递归与非递归实现

迭代实现二分查找

public int bsearch(int[] a, int n, int value) {
  int low = 0;
  int high = n - 1;

  while (low <= high) {
    int mid = (low + high) / 2;
    if (a[mid] == value) {
      return mid;
    } else if (a[mid] < value) {
      low = mid + 1;
    } else {
      high = mid - 1;
    }
  }

  return -1;
}

循环退出条件

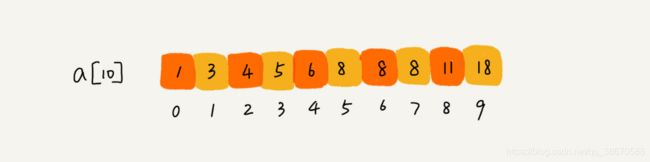
注意是 low<=high，而不是 low

mid的取值

实际上，mid=(low+high)/2 这种写法是有问题的。因为如果 low 和 high 比较大的话，两者之和就有可能会溢出。改进的方法是将 mid 的计算方式写成 low+(high-low)/2。更进一步，如果要将性能优化到极致的话，我们可以将这里的除以 2 操作转化成位运算 low+((high-low)>>1)。因为相比除法运算来说，计算机处理位运算要快得多。

low 和 high 的更新

low=mid+1，high=mid-1。注意这里的 +1 和 -1，如果直接写成 low=mid 或者 high=mid，就可能会发生死循环。比如，当 high=3，low=3 时，如果 a[3]不等于 value，就会导致一直循环不退出。

递归实现二分查找

// 二分查找的递归实现
public int bsearch(int[] a, int n, int val) {
  return bsearchInternally(a, 0, n - 1, val);
}

private int bsearchInternally(int[] a, int low, int high, int value) {
  if (low > high) return -1;

  int mid =  low + ((high - low) >> 1);
  if (a[mid] == value) {
    return mid;
  } else if (a[mid] < value) {
    return bsearchInternally(a, mid+1, high, value);
  } else {
    return bsearchInternally(a, low, mid-1, value);
  }
}

二分查找的局限性

• 二分查找依赖的是顺序表结构，简单点说就是数组。二分查找算法需要按照下标随机访问元素，二分查找只能用在数据是通过顺序表来存储的数据结构上。
• 二分查找针对的是有序数据。
• 数据量太小不适合二分查找。

2算法流程

• 如果目标值等于中间元素，则找到目标值。
• 如果目标值较小，继续在左侧搜索。
• 如果目标值较大，则继续在右侧搜索。
  
  **注意：**在计算左右端点的中点时，最简单地方法是$middle=(left+right)/2$，这样写会导致数组越界，换成另一种写法：$middle=left+(right-left)/2$

四种常见的二分查找变形问题

• 查找第一个值等于给定值的元素
• 查找最后一个值等于给定的元素
• 查找第一个大于等于给定值的元素
• 查找最后一个小于等于给定值的元素

查找第一个值等于给定值的元素

若数组中不存在重复的元素，即是简单的二分查找算法，若数组中存在重复数据，则简单的二分查找代码无法工作，如下图。

public int bsearch(int[] a, int n, int value) {
  int low = 0;
  int high = n - 1;
  while (low <= high) {
    int mid =  low + ((high - low) >> 1);
    if (a[mid] > value) {
      high = mid - 1;
    } else if (a[mid] < value) {
      low = mid + 1;
    } else {
      if ((mid == 0) || (a[mid - 1] != value)) return mid;
      else high = mid - 1;
    }
  }
  return -1;
}

改写为

public int bsearch(int[] a, int n, int value) {
  int low = 0;
  int high = n - 1;
  while (low <= high) {
    int mid =  low + ((high - low) >> 1);
    if (a[mid] > value) {
      high = mid - 1;
    } else if (a[mid] < value) {
      low = mid + 1;
    } else {
      if ((mid == 0) || (a[mid - 1] != value)) return mid;
      else high = mid - 1;
    }
  }
  return -1;
}

对于 a[mid]>value 的情况，我们需要更新 high= mid-1；
对于 a[mid] 当 a[mid]=value 的时，如果 mid 等于 0，那这个元素已经是数组的第一个元素，那它肯定是我们要找的；如果 mid 不等于 0，但 a[mid]的前一个元素 a[mid-1]不等于 value，那也说明 a[mid]就是我们要找的第一个值等于给定值的元素。

其它写法

    int low_bound(vector<int>& nums, int target) {
        int left = 0, right = nums.size(), mid;
        while (left < right) {
            mid = left + (right - left) / 2;
            if (nums[mid] >= target) {
                right = mid;
            }
            else {
                left = mid + 1;
            }
        }
        return left;
    }

查找最后一个元素等于给定值

将上述查找第一个值等于给定值的元素代码更改下即可。

public int bsearch(int[] a, int n, int value) {
  int low = 0;
  int high = n - 1;
  while (low <= high) {
    int mid =  low + ((high - low) >> 1);
    if (a[mid] > value) {
      high = mid - 1;
    } else if (a[mid] < value) {
      low = mid + 1;
    } else {
      if ((mid == n - 1) || (a[mid + 1] != value)) return mid;
      else low = mid + 1;
    }
  }
  return -1;
}

其它写法

int upper_bound(vector<int>& nums, int target) {
    int left = 0, right = nums.size(), mid;
    while (left < right) {
        mid = left + (right - left) / 2;
        if (nums[mid] > target) {
            right = mid;
        }
        else {
            left = mid + 1;
        }
    }
    return left - 1;
}

查找第一个大于等于给定值的元素

public int bsearch(int[] a, int n, int value) {
  int low = 0;
  int high = n - 1;
  while (low <= high) {
    int mid =  low + ((high - low) >> 1);
    if (a[mid] >= value) {
      if ((mid == 0) || (a[mid - 1] < value)) return mid;
      else high = mid - 1;
    } else {
      low = mid + 1;
    }
  }
  return -1;
}

查找最后一个小于等于给定值的元素

public int bsearch7(int[] a, int n, int value) {
  int low = 0;
  int high = n - 1;
  while (low <= high) {
    int mid =  low + ((high - low) >> 1);
    if (a[mid] > value) {
      high = mid - 1;
    } else {
      if ((mid == n - 1) || (a[mid + 1] > value)) return mid;
      else low = mid + 1;
    }
  }
  return -1;
}

4LeetCode题型总结

• 704. 二分查找
• 剑指 Offer 53 - II. 0～n-1中缺失的数字

题型总结目录

题型总结——前K系列（堆、优先队列）.
题型总结——二分查找（中间点计算的改进）.
题型总结——二维数组（矩阵）之逆逆时针输出、查找.
题型总结——栈的应用.
题型总结——双指针算法全部模型（持续更新）.