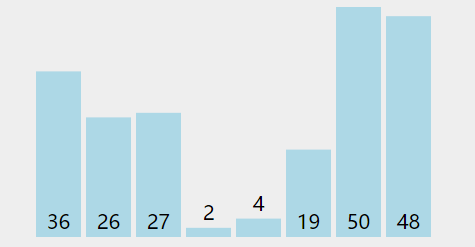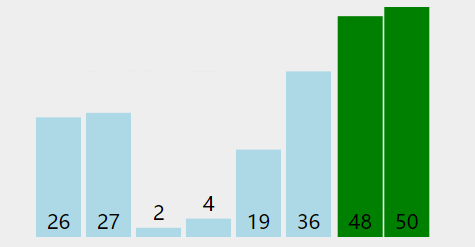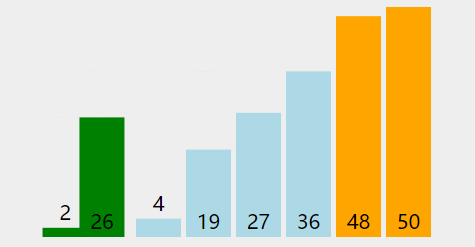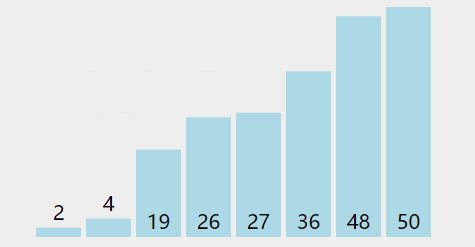【排序】插入排序、冒泡排序、选择排序
排序的概念
排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。
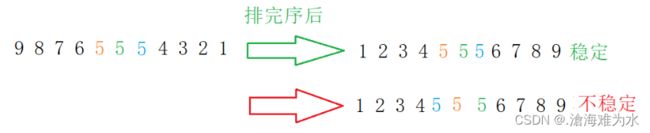
稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的。
内部排序:数据元素全部放在内存中的排序。
外部排序:数据元素太多不能同时放在内存中,根据排序过程的要求不能在内外存之间移动数据的排序。
常见的排序算法
本篇博客就先讲三个N^2级别的排序,虽然时间复杂度比较拉,但是对于初学者来说还是很有学习的必要的。
那么这三个排序讲完后,紧接着就会讲时间复杂读为N*logN的三个排序,在讲二叉树的时候顺便把堆排序也给讲了。然后就剩下三个重量级的排序了:希尔,快排,归并都是非常重要的。下面的例子都是以排升序来演示的。
插入排序
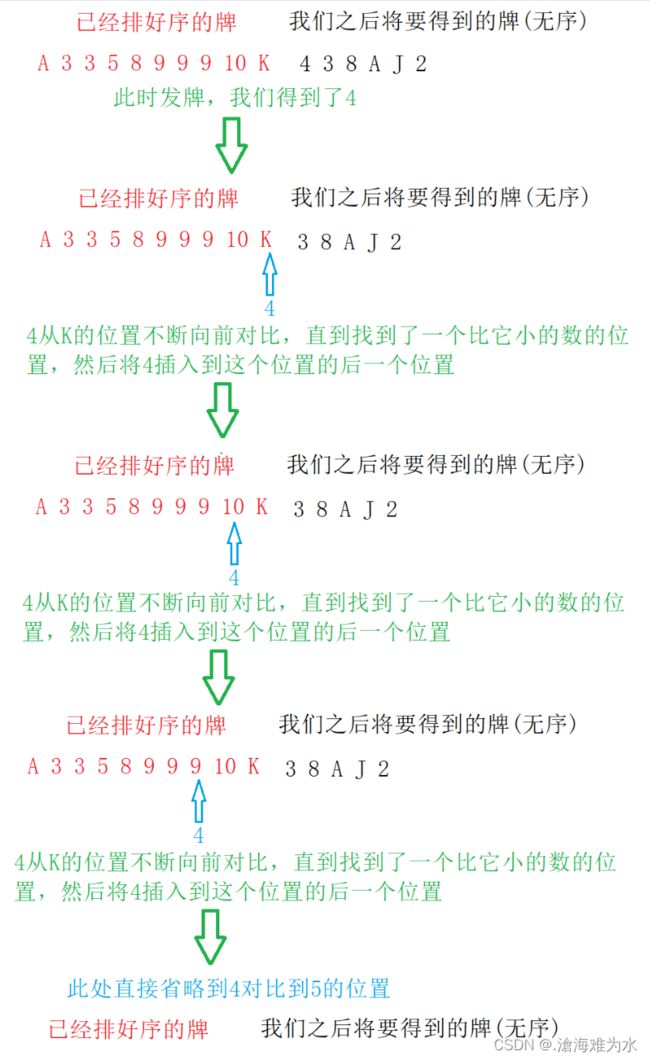
相信大家都打过扑克牌,那么当我们在不断接收牌的时候就需要对所接受的牌的顺序进行整理,从A到K(可能也有大小王),那么我们每接收到一张牌就要将这张牌插入到我们之前整理好的排中,比如说我现在手里有的牌是 A 3 3 5 8 9 9 9 10 K,当我们接收到了一张4的时候,我们就要将这张4放到其对应的位置上,也就是3和5之间,那么整理过后的牌就是 A 3 3 4 5 8 9 9 9 10 K。
我们再以上面的例子来想一想,其实当我们接收到4的时候,4是从我们还未接收到的排中选出来的,对应到我们上面的图解中的话,4就是后方所有无序中的数中的第一个,那么我们跳出来了这个数,要和前方有序的数挨个对比,直到找到了适合它的位置的时候就停下来,插入到这个位置,那么这样的思想其实就是插入排序的思想。
那么大概的思想就是每趟从无序的数里面选出第一个数,然后将这个数插入到排好序的数中。一共只需要走n-1趟。
代码实现思路
一共定义三个变量:
- 一个是end,用来代表有序数中的最后一个数的位置 。
- 一个是end+1,代表无序数中的第一个数的位置。
- 一个是key,存放的是end+1位置上的数,也就是无序数中的第一个数。
每次对比end位置上的数和key位置上的数,对比的时候无非三种情况:
- 如果end位置上的数比key大了,就让end位置上的数放到end+1位置上,然后让end–。
- 如果end位置上的数比key小了,就直接停,把key放到end + 1的位置上。
- 如果end越界(end不断减小,就可能导致end <0),就直接将key放到end + 1的位置上。
这上面的两种情况都是针对某一单趟来排序的,那么我们如果要排序的话,应该从第一个位置开始排,然后到第n-1个数排好后就完成了。
//插入排序
void InsertSort(int* a, int n)
{
assert(a);
for (int i = 0; i < n - 1; i++)
{
//单趟排
int end = i;
int key = a[end + 1];
while (end >= 0)
{
//遇到大的就把大的数往后挪
if (a[end] > key)
a[end + 1] = a[end];
else//遇到小的就直接跳出循环
break;
//只有遇到大的才会让end--继续对比前面的数
end--;
}
//不管是end越界还是遇到了小的数,就直接让end+1的位置赋值为key
a[end + 1] = key;
}
}
时间复杂度分析
首先我在最前面已经给出了这三个排序都是N^2级别的排序,那么我就简单说一下这三个的最好的情况是多少。
当一个数据是有序的情况下我们进行排序时,插入排序每次对比的次数就只有一次,所以赋值的操作也就只有一次就可以了,这种情况下,插入排序是最牛的,时间复杂度是O(N)。
数据接近有序的时候也是,对比的次数会很少,几乎就是O(N)了,但是正常情况下还是O(N^2)。
有的人可能会说有序了还排什么序呢?
请注意,如果我给了你一组非常大的数据,你能够一眼看出来这组数有序吗?答案肯定是不能的,如果仅仅给了你100个有序的数,怕是都要个几十秒你才能确定这些数是有序的,但如果给机器的话那就是以毫秒来计算了,可能人家一毫秒就计算出来了。
所以不要在这里犟嘴说有序的为什么要排序,你要是能一眼看出来10万个数有序的话,那就不需要机器了。
所以说,当一组数有序或者接近有序的时候,插入排序可以起到非常大的作用,有时甚至比快排(快速排序)还猛。
插入排序也是这三个N^2级别的排序中最优的那一个排序。
冒泡排序
冒泡排序对于新手来说应该是非常熟悉的排序了,我们学校里面开C语言的时候非常看重冒泡排序,其实它的思想对于小白来说也是很重要的,既然比较熟悉我就不说的那么详细了。
以某一趟排序来说,第一个位置与第二个位置进行比较,如果其哪一个比后一个大,就交换这两个数,然后继续往后比较,如果前一个比后一个小,就继续比较后面的。
每趟排序都能将最大的那个数放到后面有序数中的第一个位置。
//冒泡排序
void BubbleSort(int* a, int n)
{
assert(a);
for (int j = 0; j < n - 1; j++)
{
//falg用来判断当前这趟排序是否发生了交换
//如果发生了交换,那么本趟排序不能说明数组已经有序
//如果没有发生交换,那么就说明数组已经有序
int flag = 0;
//单趟
for (int i = 0; i < n - 1 - j; i++)
{
if (a[i] > a[i + 1])
{
swap(&a[i], &a[i + 1]);
flag = 1;
}
}
//本趟排序结束后没有发生交换,数组已经有序
if (flag == 0)
break;
}
}
时间复杂度分析
当数组完全有序的时候,才能到达O(N),当数组不完全有序,随随便便就是O(N^2)了,很一般的排序。
选择排序
择排序的思路是最简单的,就是每趟选出一个最值,然后将这个最值放到某一段。
如果你排的是升序,那么每次选出最大值放到最右端或者每次选出最小值放到最左端。如果你排的是降序,那么每次选出最大值放到最左端或者每次选出最小值放到最右端。
很简单,不过多赘述,但我们可以稍微优化一下,就是每次把最小值和最大值都选出来,然后放在两端,这样的话每次排好序的就是两个数,而不是上面每趟排一个数。
//选择排序
void SelectSort(int* a, int n)
{
//选出无序的左右两端,然后left和right之间的数是无序的
//left和right两边的数是有序的,left左边就是小的数,right右边就是大的数
int left = 0;
int right = n - 1;
while (left < right)
{
//单趟
int maxi = left, mini = left;
for (int i = left + 1; i <= right; i++)
{
if (a[maxi] < a[i])
maxi = i;
if (a[mini] > a[i])
mini = i;
}
swap(&a[maxi], &a[right]);
//如果出现mini在最右端的情况,也就是right等于了mini
//那么我们在交换a[maxi]和a[right]的时候就会把a[mini]也换走了
//这时候就要把mini修正一下,防止在left和mini上的数交
//换的时候把maxi给换到left的位置上去了。
if (right == mini)
mini = maxi;
swap(&a[mini], &a[left]);
left++;
right--;
}
}
时间复杂度分析
选择排序是最差的,因为当数组有序的时候是无法判断的,不管有没有序都要选最值,然后再放到对应的位置,所以当数组有序的时候也是O(N^2)的。
稳定性
稳定性是值当一个数在所有数据中出现两次及以上的话,排完序后这几个数的相对位置不会改变,这样的排序就是稳定的。
这里就直接给结论了:插入和冒泡是稳定的。选择不稳定。
总结
这三个排序中,最厉害的是插入排序,最优情况下可以达到O(N),也是我讲的最细的一个排序,因为这个排序的代码绕了一点。希尔排序这个排序就比较厉害了,希尔排序的思想是基于插入排序的。冒泡排序和选择排序的时间复杂度都比较拉,会了就行,没什么厉害的地方。