机器人学、机器视觉与控制 上机笔记(2.1章节)
机器人学、机器视觉与控制 上机笔记(2.1章节)
- 1、前言
- 2、本篇内容
- 3、代码记录
-
- 3.1、新建se2
- 3.2、生成坐标系
- 3.3、将T1表示的变换绘制
- 3.4、完整绘制代码
- 3.5、获取点`*`在坐标系1下的表示
- 3.6、相对坐标获取完整代码
- 4、结语
1、前言
工作需要,想同时显示出六轴协作臂,一组位姿信息逆解出的八组关节角的效果情况。就想使用MATLAB的机器人工具箱RTB去实现这一需求,辅助数据分析。朋友推荐了《机器人学、机器视觉与控制》这本书,书的作者也是工具箱RTB的作者,就开始拜读补充基础知识,并结合书中的RTB示例代码熟悉RTB的使用。个人使用的matlab2022b版本和10.4版本的RTB,实际操作时发现书本中的示例代码(猜测应该是9版本的RTB,语法未做到向下兼容)在个人使用的环境下,频繁出现报错无法运行的问题。就准备写一个改正后的实机运行记录系列。
2、本篇内容
记录书中第2.1章节中的示例代码,修改后能在10.4版本中正确运行。
3、代码记录
3.1、新建se2
原书中的第一步是用函数se2创建一个齐次变换,原书代码如下:
>> T1 = se2(1, 2, 30 * pi / 180)
T1 =
0.8660 -0.5000 1.0000
0.5000 0.8660 2.0000
0 0 1.0000
在高位版本环境下,运行报错,原因是se2的函数形参变动调整了
>> T1 = se2(1, 2, 30 * pi / 180)
错误使用 matlabshared.spatialmath.internal.SE2Base
Invalid number of arguments. To create an se2, specify 2 or fewer arguments.
出错 se2 (第 69 行)
obj@matlabshared.spatialmath.internal.SE2Base(varargin{:});
下面我们来看看help文档中,高版本的se2函数定义:
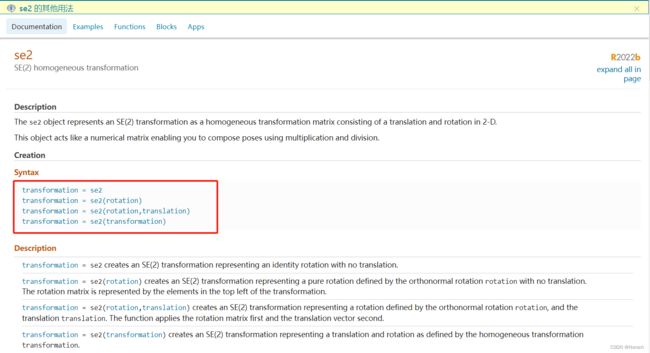
原书中是位移在前,旋转在后,高版本恰恰相反了。因此,新建se2需要修改为(可能步骤有些繁琐,欢迎评论区留言优化):
>> tr = [1, 2]
tr =
1 2
>> rot = rotz(30)
rot =
0.8660 -0.5000 0
0.5000 0.8660 0
0 0 1.0000
>> T1 = se2(rot(1:2, 1:2), tr)
T1 =
se2
0.8660 -0.5000 1.0000
0.5000 0.8660 2.0000
0 0 1.0000
3.2、生成坐标系
这个没有问题,同原书一样即可,生成一个XY轴分别为[0,5]刻度的二维平面坐标系。
>> axis([0 5 0 5]);
3.3、将T1表示的变换绘制
原书代码如下:
>> trplot2(T1, 'frame', '1', 'color', 'b')
在高位版本下,同样运行报错,报错提示如下:
>> trplot2(T1, 'frame', '1', 'color', 'b')
Unable to perform assignment because value of type 'se2' is not convertible to 'double'.
出错 transl (第 88 行)
t1(1:3,4,:) = x';
出错 trplot2 (第 148 行)
if all(size(T) == [3 3]) || norm(transl(T)) < eps
原因:
无法从 se2 转换为 double。
根据报错提示,T1此时是se2数据类型,而高版本的trplot2函数的第一个形参,要求数据类型为double,那么,此处需要手动进行数据类型转换。可以参考该链接: (知乎)matlab中SE3是什么类型,怎么转换成double型矩阵?
经过实际尝试,使用tform函数有效,转换如下:
>> T1_double = tform(T1)
T1_double =
0.8660 -0.5000 1.0000
0.5000 0.8660 2.0000
0 0 1.0000
工作区中也可以观察到,数据类型变换成功。

这边需要再多说几句,知乎回答中提及的T1.T方式尝试过,报错未识别类 'se2' 的方法、属性或字段 'T'。,提及的另一种double(T1)强制转换的方式也同样以失败告终。之后翻阅了tform函数的文档看了一下,该函数应该是2022b版本以后引入的。

最终运行效果如下,记得补加上hold on,原书中缺失,不然坐标轴刻度变化,不再是[0,5]:
>> T1_double = tform(T1)
T1_double =
0.8660 -0.5000 1.0000
0.5000 0.8660 2.0000
0 0 1.0000
>> hold on
>> trplot2(T1_double, 'frame', '1', 'color', 'b')
3.4、完整绘制代码
>> tr = [1, 2]
tr =
1 2
>> rot = rotz(30)
rot =
0.8660 -0.5000 0
0.5000 0.8660 0
0 0 1.0000
>> T1 = se2(rot(1:2, 1:2), tr)
T1 =
se2
0.8660 -0.5000 1.0000
0.5000 0.8660 2.0000
0 0 1.0000
>> axis([0 5 0 5]);
>> T1_double = tform(T1)
T1_double =
0.8660 -0.5000 1.0000
0.5000 0.8660 2.0000
0 0 1.0000
>> hold on
>> trplot2(T1_double, 'frame', '1', 'color', 'b')
>> rot2 = rotz(0)
rot2 =
1 0 0
0 1 0
0 0 1
>> tr2 = [2, 1]
tr2 =
2 1
>> T2 = se2(rot2(1:2, 1:2), tr2)
T2 =
se2
1 0 2
0 1 1
0 0 1
>> T2_double = tform(T2)
T2_double =
1 0 2
0 1 1
0 0 1
>> hold on
>> trplot2(T2_double, 'frame', '2', 'color', 'r');
>> T3 = T1 * T2
T3 =
se2
0.8660 -0.5000 2.2321
0.5000 0.8660 3.8660
0 0 1.0000
>> T3_double = tform(T3)
T3_double =
0.8660 -0.5000 2.2321
0.5000 0.8660 3.8660
0 0 1.0000
>> hold on;
>> trplot2(T3_double, 'frame', '3', 'color', 'g');
>> T4 = T2 * T1
T4 =
se2
0.8660 -0.5000 3.0000
0.5000 0.8660 3.0000
0 0 1.0000
>> T4_double = tform(T4)
T4_double =
0.8660 -0.5000 3.0000
0.5000 0.8660 3.0000
0 0 1.0000
>> hold on
>> trplot2(T4_double, 'frame', '4', 'color', 'c')
>> hold on;
>> P = [3; 2];
>> plot_point(P, '*');
3.5、获取点*在坐标系1下的表示
原书中的inv,在高版本使用时同样需要注意数据类型一致的问题:
% 原书中使用的变量名为P1
% 个人使用P_to_T1替换,感觉变量名意义更清晰明了些
>> P_to_T1 = inv(T1) * [P; 1]
错误使用 .*
times, .* requires both operands to be transformations or rotations (of the same type).
出错 * (第 18 行)
out = obj1 .* obj2;
报错原因为左侧inv(T1)的结果仍为se2类型,需要变为double类型。验证如下:
>> Test = inv(T1)
Test =
se2
0.8660 0.5000 -1.8660
-0.5000 0.8660 -1.2321
0 0 1.0000
>> Test_double = tform(Test)
Test_double =
0.8660 0.5000 -1.8660
-0.5000 0.8660 -1.2321
0 0 1.0000
>> P_to_T1 = Test_double * [P; 1]
P_to_T1 =
1.7321
-1.0000
1.0000
成功获取,点*相对于坐标系{1}的表示为(1.7321,-1.0000)。
3.6、相对坐标获取完整代码
>> Test = inv(T1)
Test =
se2
0.8660 0.5000 -1.8660
-0.5000 0.8660 -1.2321
0 0 1.0000
>> Test_double = tform(Test)
Test_double =
0.8660 0.5000 -1.8660
-0.5000 0.8660 -1.2321
0 0 1.0000
>> P_to_T1 = Test_double * [P; 1]
P_to_T1 =
1.7321
-1.0000
1.0000
>> h2e(Test_double * e2h(P))
ans =
1.7321
-1.0000
>> homtrans(Test_double, P)
ans =
1.7321
-1.0000
>> P_to_T2 = homtrans(tform(inv(T2)), P)
P_to_T2 =
1
1
4、结语
平时工作为机械臂软件开发,书本中的matlab示例代码跑通的感觉还是挺舒服的。2.1节总体评价不错,通过二维演示了三维常见的齐次变换大致的使用思想。减去Z的维度,确实更方便初学者的理解。工作一年多,回过头来再看这些内容,也受益匪浅。


