编译原理实验2——自上而下语法分析LL1(包含去消除左递归、消除回溯)
文章目录
-
- 实验目的
- 实现流程
-
- 代码
- 运行结果
-
- 测试1(含公共因子)
- 测试2(经典的i+i*i文法,且含左递归)
- 测试3(识别部分标识符)
- 总结
实验目的
实现自上而下分析的LL1语法分析器,给出分析过程
实现流程
代码
代码逻辑
1.预处理
- 去除多余空格:如“ S - > aB”,处理成“S-> aB”
- 拆解候选式:对于某一产生式,若有多个候选式,根据 | 符号拆解为多个产生式。
- 获取开始符号:默认输入的第一个非终结符为开始符
- 消除左递归和回溯(公共因子)
- 获取非终结符和终极符
2.计算first集和follow集
3.检查是否符合LL1文法
4.建立预测分析表
5.对输入串进行LL1分析
import copy
from collections import defaultdict
import pandas as pd
class LL1:
def __init__(self, input_str_list):
self.input_str_list = input_str_list
self.formulas_dict = {} # 存储产生式 ---dict 形式
self.S = "" # 开始符
self.Vt = [] # 终结符
self.Vn = [] # 非终结符
self.first = defaultdict(set) # 初始化First集合
self.follow = defaultdict(set) # 初始化Follow集合
self.table = {} # 预测分析表
self.info = {}
# 消除直接左递归
def eliminate_direct_left_recursion(self, grammar, non_terminal):
productions = grammar[non_terminal]
recursive_productions = []
alphabet_list = [chr(i) for i in range(ord('A'), ord('Z') + 1)] # A-Z,用于给新非终结符命名
for production in productions: # 找到含有左递归的候选式
if production.startswith(non_terminal):
recursive_productions.append(production)
if len(recursive_productions) > 0:
# 命名为A-Z且不与原有存在的非终结符重名
for ch in alphabet_list:
if ch not in grammar.keys():
new_non_terminal = ch
break
# S = Sab \ Scd \ T \ F
# 更新原始非终结符的产生式 S = (T\F) S'
grammar[non_terminal] = [p + new_non_terminal for p in productions if not p.startswith(non_terminal)]
# 添加新的非终结符的产生式 S'=(ab\cd) S'
grammar[new_non_terminal] = [p[1:] + new_non_terminal for p in recursive_productions if
p.startswith(non_terminal)]
grammar[new_non_terminal].append('@') # S'=(ab\cd)S' \ @
return grammar
# 往后预测,看是否会出现间接左递归
def is_recruse(self, grammar, non_terminals, iidx, cur, pre):
# print(f"=====cur:{cur}, pre:{pre}=====")
check = False
set_front_con = set() # pre右侧所有可能递归的vn
for pre_production in grammar[pre]:
if pre_production[0].isupper():
set_front_con.add(pre_production[0])
# print("pre_set:", set_front_con)
set_back_con = set()
for i in range(iidx, len(non_terminals)): # 遍历所有非终结符 curback = cur......最后一个终结符
cur_back = non_terminals[i]
# print("cur_back", cur_back)
if i == len(non_terminals) - 1: # 若为最后一个终结符,则加入自身
set_back_con.add(cur_back)
for cur_back_pro in grammar[cur_back]: # 遍历当前cur_back的候选式
if cur_back_pro.startswith(cur):
set_back_con.add(cur_back)
# print("cur_set:", set_back_con)
if len(set_front_con & set_back_con) != 0: # 有交集
check = True
return check
# 消除左递归(先间接后直接)
def eliminate_left_recursion(self, grammar):
non_terminals = list(grammar.keys())[::-1] # 逆序,将开始符放到最后
replaced_vn = [] # 记录被替换代入掉的非终结符
for i in range(len(non_terminals)): # 遍历所有非终结符
cur = non_terminals[i]
# 间接左递归--》直接左递归
for j in range(i): # 遍历 pre1,pre2,pre3.....cur的非终结符(cur前面的终结符)
pre = non_terminals[j]
new_productions = []
for cur_production in grammar[cur]:
if cur_production.startswith(pre): # 在cur的所有候选式中,找到以pre开头的候选式
if self.is_recruse(grammar, non_terminals, i, cur, pre): # 若最终能产生间接左递归,进行代入合并处理
rest_str = cur_production.replace(pre, '', 1) # 截取cur的该候选式去除首字符后的剩余字符
replaced_vn.append(pre)
for pre_production in grammar[pre]: # 加入到pre的所有候选式后面
if pre_production + rest_str not in new_productions:
new_productions.append(pre_production + rest_str)
else: # 不进行代入合并处理
if cur_production not in new_productions:
new_productions.append(cur_production)
else:
if cur_production not in new_productions:
new_productions.append(cur_production)
grammar[cur] = new_productions
grammar = self.eliminate_direct_left_recursion(grammar, cur) # 消除当前的直接左递归
# 消除冗余产生式(那些被替换代入的产生式)
for vn in replaced_vn:
del grammar[vn]
return grammar
# 消除回溯
def eliminate_huisu(self, grammar):
alphabet_list = [chr(i) for i in range(ord('A'), ord('Z') + 1)] # A-Z,用于给新非终结符命名
while True:
grammar_copy = grammar.copy()
for left, right in grammar_copy.items():
right = list(right)
prefixes = []
# 找所有项目的公共因子
for i in range(len(right)):
for j in range(i + 1, len(right)):
str1, str2 = right[i], right[j]
index = 0
while index < min(len(str1), len(str2)) and str1[index] == str2[index]:
index += 1
if index >= 1:
have = False
for pre in prefixes:
if pre[0] == str1[0]:
have = True
if not have:
if str1[:index] not in prefixes:
prefixes.append(str1[:index])
# =================================================================
if len(prefixes) == 0:
continue
tmp_match = defaultdict(set)
tmp_not_match = set()
# for pre in prefixes:
# for r_candidate in right:
# if r_candidate.startswith(pre):
# tmp_match[pre].add(r_candidate)
for r_candidate in right:
match=False
for pre in prefixes:
if r_candidate.startswith(pre):
tmp_match[pre].add(r_candidate)
match=True
break
if not match:
tmp_not_match.add(r_candidate)
new_ini_pro = set()
for vn, right in tmp_match.items():
new_r_pro = []
new_vn = ""
for r_candidate in right:
for ch in alphabet_list: # 根据alphabet_list给new_vn命名
if ch not in grammar.keys():
new_vn = ch
break
if r_candidate[len(vn):] == "": # 切片后为空(即只剩一个字符),则新产生式补@
if "@" not in new_r_pro:
new_r_pro.append('@')
else:
if r_candidate[len(vn):] not in new_r_pro:
new_r_pro.append(r_candidate[len(vn):])
grammar[new_vn] = new_r_pro
new_ini_pro.add(vn + new_vn)
grammar[left] = list(new_ini_pro.union(tmp_not_match))
# print(grammar)
if grammar_copy == grammar: # 不再发生改变,则退出while
break
return grammar
# 预处理
def step1_pre_process(self, grammar_list):
formulas_dict = {} # 存储产生式 ---dict 形式
S = " " # 开始符
Vt = [] # 终结符
Vn = [] # 非终结符
for production in grammar_list:
left, right = production.split('->')
if "|" in right:
r_list = right.split("|")
formulas_dict[left] = []
for r in r_list:
if r not in formulas_dict[left]:
formulas_dict[left].append(r)
else:
if left in formulas_dict.keys():
formulas_dict[left].append(right)
else:
formulas_dict[left] = [right] # 若left不存在,会自动创建 left: 空set
# 文法开始符
S = list(formulas_dict.keys())[0]
# 消除左递归和回溯
formulas_dict = self.eliminate_left_recursion(formulas_dict)
formulas_dict = self.eliminate_huisu(formulas_dict)
print("=========消除左递归和回溯后的产生式=========")
for left,right in formulas_dict.items():
print(left+"->"+"".join(right))
print("=========基本信息=========")
# 获取终结符和非终结符
for left, right in formulas_dict.items():
if left not in Vn:
Vn.append(left)
for r_candidate in right:
for symbol in r_candidate:
if not symbol.isupper() and symbol != '@':
if symbol not in Vt:
Vt.append(symbol)
# 打印非终结符和终结符
print("开始符:", S)
print("非终结符:", Vn)
print("终结符:", Vt)
return formulas_dict, Vn, Vt, S
def cal_symbol_first(self, symbol):
# 如果是终结符,直接加入到First集合
if not symbol.isupper():
self.first[symbol].add(symbol)
else:
for r_candidate in self.formulas_dict[symbol]:
i = 0
while i < len(r_candidate):
next_symbol = r_candidate[i]
# 如果是非终结符,递归计算其First集合
if next_symbol.isupper():
self.cal_symbol_first(next_symbol)
self.first[symbol] = self.first[symbol].union(
self.first[next_symbol] - {'@'}) # 合并first(next_symbol)/{@}
if '@' not in self.first[next_symbol]:
break
# 如果是终结符,加入到First集合
else:
self.first[symbol].add(next_symbol)
break
i += 1
# 如果所有符号的First集合都包含ε,将ε加入到First集合
if i == len(r_candidate):
self.first[symbol].add('@')
# 计算First集合
def step2_cal_first(self, formulas_dict):
# 计算所有非终结符的First集合
for vn in formulas_dict.keys():
self.cal_symbol_first(vn)
# 计算所有终结符的First集合
for vt in self.Vt:
self.cal_symbol_first(vt)
# 计算ε的First集
self.cal_symbol_first('@')
# 打印First集合
for key, value in self.first.items():
print(f"First({key}): {value}")
# 计算Follow集合1——考虑 添加first(Vn后一个非终结符)/{ε}, 而 不考虑 添加follow(left)
def cal_follow1(self, vn):
self.follow[vn] = set()
if vn == self.S: # 若为开始符,加入#
self.follow[vn].add('#')
for left, right in self.formulas_dict.items(): # 遍历所有文法,取出左部单Vn、右部候选式集合
for r_candidate in right: # 遍历当前 右部候选式集合
i = 0
while i <= len(r_candidate) - 1: # 遍历当前 右部候选式
if r_candidate[i] == vn: # ch == Vn
if i + 1 == len(r_candidate): # 如果是最后一个字符 >>>>> S->....V
self.follow[vn].add('#')
break
else: # 后面还有字符 >>>>> S->...V..
while i != len(r_candidate):
i += 1
if r_candidate[i] == vn: # 又遇到Vn,回退 >>>>> S->...V..V..
i -= 1
break
if r_candidate[i].isupper(): # 非终结符 >>>>> S->...VA..
self.follow[vn] = self.follow[vn].union(self.first[r_candidate[i]] - {'@'})
if '@' in self.first[r_candidate[i]]: # 能推空 >>>>> S->...VA.. A可推空
if i + 1 == len(r_candidate): # 是最后一个字符 >>>>> S->...VA A可推空 可等价为 S->...V
self.follow[vn].add('#')
break
else: # 不能推空 >>>>> S->...VA.. A不可推空
break
else: # 终结符 >>>>> S->...Va..
self.follow[vn].add(r_candidate[i])
break
else:
i += 1
# 计算Follow集合2——考虑 添加follow(left)
def cal_follow2(self, vn):
for left, right in self.formulas_dict.items(): # 遍历所有文法,取出左部单Vn、右部候选式集合
for r_candidate in right: # 遍历当前 右部候选式集合
i = 0
while i <= len(r_candidate) - 1: # 遍历当前 右部候选式
if r_candidate[i] == vn: # 找到Vn
if i == len(r_candidate) - 1: # 如果当前是最后一个字符,添加 follow(left) >>>>> S->..V
self.follow[vn] = self.follow[vn].union(self.follow[left])
break
else: # 看看后面的字符能否推空 >>>>> S->..V..
while i != len(r_candidate):
i += 1
if '@' in self.first[r_candidate[i]]: # 能推空 >>>>> S->..VB.. B可推空
if i == len(r_candidate) - 1: # 且是最后一个字符 >>>>> S->..VB B可推空
self.follow[vn] = self.follow[vn].union(self.follow[left])
break
else: # 不是最后一个字符,继续看 >>>>> S->..VBA.. B可推空
continue
else: # 不能推空 >>>>> S->..VB.. B不可为空
break
i += 1
# 计算所有Follow集合的总长度,用于判断是否还需要继续完善
def cal_follow_total_Len(self):
total_Len = 0
for vn, vn_follow in self.follow.items():
total_Len += len(vn_follow)
return total_Len
def step3_cal_follow(self, formulas_dict):
# 先用 cal_follow1 算
for vn in formulas_dict.keys():
self.cal_follow1(vn)
# 在循环用 cal_follow2 算, 直到所有follow集总长度不再变化,说明计算完毕
while True:
old_len = self.cal_follow_total_Len()
for vn in formulas_dict.keys():
self.cal_follow2(vn)
new_len = self.cal_follow_total_Len()
if old_len == new_len:
break
# 打印Follow集合
for key, value in self.follow.items():
print(f"Follow({key}): {value}")
# 检测是否符合LL(1)文法
def step4_check_LL1(self, formulas_dict, first, follow):
# 检查每个产生式右部,多个候选式中每个候选首字符的first集是否相交(回溯)
for left, right in formulas_dict.items():
if len(right) >= 2:
# print(f"{left}: {right}")
s = set()
for r_candidate in right:
old_len = len(s)
s = s.union(first[r_candidate[0]])
new_len = len(s)
if old_len == new_len:
return False
# 每个产生式A,若饿ε∈first(A),则first(A) ∩ follow(A) = 空集
for left, right in formulas_dict.items():
if '@' in first[left]:
if first[left] & follow[left]: # 有交集
return False
return True
# 建立LL(1)预测分析表
def step5_create_table(self, formulas_dict, first, follow):
tab_dict = {}
for left, right in formulas_dict.items(): # 对于每一个产生式,求出其每个候选式的first集
for r_candidate in right:
idx=0
cur_can_first = set()
while True:
if r_candidate[idx].isupper():
cur_can_first = cur_can_first.union(first[r_candidate[idx]] - {'@'})
else:
cur_can_first.add(r_candidate[idx])
idx += 1
if idx >= len(r_candidate) or ('@' not in first[r_candidate[idx-1]]):
break
for fi in cur_can_first:
if fi == '@':
for fo in follow[left]:
tab_dict[(left, fo)] = '@'
else:
tab_dict[(left, fi)]=r_candidate
df = pd.DataFrame(list(tab_dict.items()), columns=['Key', 'Value'])
df['Vn'] = [x[0] for x in df['Key']]
df['Vt'] = [x[1] for x in df['Key']]
tab_df = df.pivot(index='Vn', columns='Vt', values='Value')
print(tab_df)
return tab_dict, tab_df
# LL1分析
def step6_LL1_analyse(self, s, S, Vn, Vt, table):
s = list(s) # 将字符串转为list类型,方便增删
s.append('#') # 末尾加入#
sp = 0 # 字符串指针
stack = [] # 栈
stack.append('#') # 进#
stack.append(S) # 进开始符
msg = "" # 分析情况
step = 0 # 步骤数
info_step, info_stack, info_str, info_msg, info_res = [], [], [], [], ""
while sp != len(s):
ch = s[sp] # 获取当前输入字符
top = stack[-1] # 获取栈顶元素
step += 1
info_step.append(step)
info_stack.append(''.join(stack))
info_str.append(''.join(s[sp:]))
info_msg.append(msg)
if top in Vt: # 栈顶元素是 终结符
if top == ch:
top = stack.pop() # 栈顶出栈
sp += 1 # str指针后移一位
msg = f"'{ch}'匹配"
else:
info_res = f"error: 栈顶元素{top} 与 字符{ch} 不匹配!"
break
elif top in Vn: # 栈顶元素是 非终结符
if (top, ch) in table.keys(): # table中含有该项
top = stack.pop() # 先出栈
stack.extend(reversed(table[(top, ch)])) # 逆序入栈
msg = f"{top}->" + table[(top, ch)]
else:
# tk_show_info += f"error: table找不到匹配的({top},{ch})\n"
info_res = f"error: table找不到匹配的({top},{ch})"
break
elif top == '#': # 栈顶元素是 文法结束符
if ch == '#':
# tk_show_info += f"Success!\n"
info_res = f"Success!"
break
else:
# tk_show_info += f"error: 栈顶元素{top} 与 字符{ch} 不匹配!\n"
info_res = f"error: 栈顶元素{top} 与 字符{ch} 不匹配!"
break
elif top == '@': # 栈顶元素是 ε
top = stack.pop() # 直接出栈ε
msg = f"'@'出栈"
continue
info = {
"info_step": info_step,
"info_stack": info_stack,
"info_str": info_str,
"info_msg": info_msg,
"info_res": info_res
}
return info
def init(self):
self.formulas_dict, self.Vn, self.Vt, self.S = self.step1_pre_process(self.input_str_list)
print("=========First、Follow=========")
self.step2_cal_first(self.formulas_dict)
self.step3_cal_follow(self.formulas_dict)
check_res = self.step4_check_LL1(self.formulas_dict, self.first, self.follow)
# =========判断是否合法=========
if check_res:
print("\n经过分析,该文法 符合 LL(1)文法\n")
else:
print("\n经过分析,该文法 不符合 LL(1)文法\n")
return
print("=========预测分析表=========")
self.table, df_tab = self.step5_create_table(self.formulas_dict, self.first, self.follow)
def solve(self,s):
self.info = self.step6_LL1_analyse(s,self.S,self.Vn,self.Vt,self.table)
print("=========分析过程=========")
for i in range(len(self.info["info_step"])):
print("{:<15} {:<15} {:<15} {:<15}".format(str(self.info["info_step"][i]), self.info["info_stack"][i],self.info["info_str"][i], self.info["info_msg"][i]))
return self.info
if __name__ == "__main__":
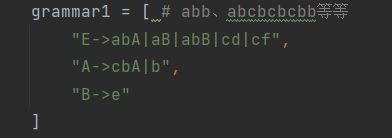
grammar1 = [ # abb、abcbcbcbb等等
"E->abA|aB|abB|cd|cf",
"A->cbA|b",
"B->e"
]
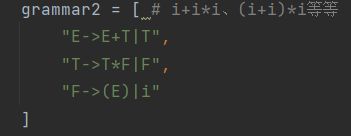
grammar2 = [ # i+i*i、(i+i)*i等等
"E->E+T|T",
"T->T*F|F",
"F->(E)|i"
]
grammar3=[ # 部分标识符文法: 形如aa、a1、aaa、aa1
"E->LL|LD|LLL|LLD",
"L->a|b|c",
"D->0|1|2|3|4|5|6|7|8|9"
]
grammar4=[ # aad、bd、cbd、aacbd等等
"S->AaS|BbS|d",
"A->a",
"B->@|c"
]
ll1 = LL1(grammar3)
ll1.init()
analyse_str="ab1"
ll1.solve(analyse_str)
运行结果
测试1(含公共因子)
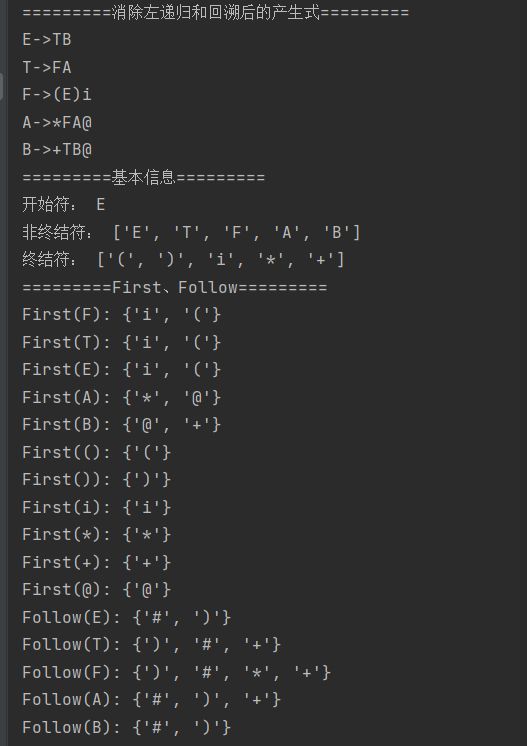
测试2(经典的i+i*i文法,且含左递归)
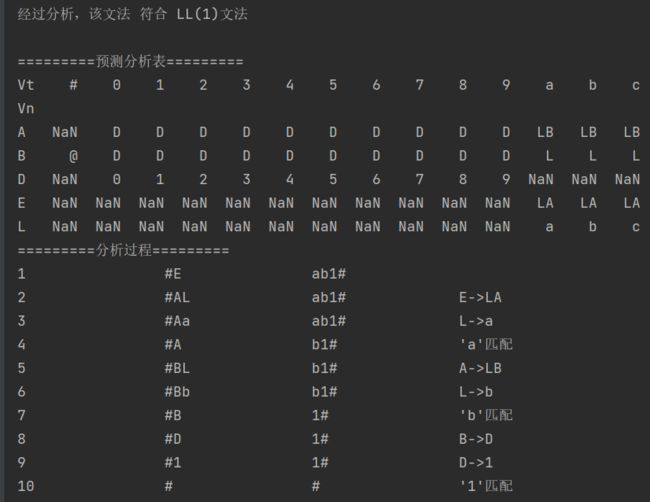
测试3(识别部分标识符)
总结
实现过程中,对于消除左递归、消除回溯、first集、follow集的实现查阅了很多资料,修改了很多次代码,目前来说暂时能适用很多文法了。