【芯片设计- RTL 数字逻辑设计入门 11.1 -- 状态机实现 移位运算与乘法 1】
文章目录
-
- 移位运算与乘法
-
- 状态机简介
- SystemVerilog中的测试平台
- VCS 波形仿真
- 阻塞赋值和非阻塞赋值
-
- 有限状态机(FSM)与无限状态机的区别
本篇文章接着上篇文章【芯片设计- RTL 数字逻辑设计入门 11 – 移位运算与乘法】 继续介绍,这里使用状态机来实现。
移位运算与乘法
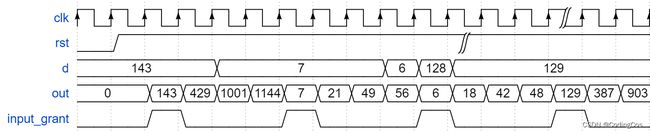
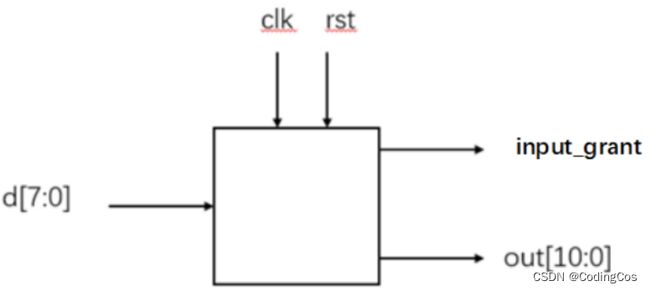
已知d为一个8位数,请在每个时钟周期分别输出该数乘1/3/7/8,并输出一个信号通知此时刻输入的d有效(d给出的信号的上升沿表示写入有效)
状态机简介
在Verilog中实现状态机通常包括三个主要部分:状态声明、状态转换和输出逻辑。状态机可以是"Moore"或"Mealy"类型,区别在于输出是仅由当前状态决定(Moore),还是由当前状态和输入决定(Mealy)。
以下是一个 错误的 Moore 状态机的 Verilog 代码示例:
module moore_state_machine(
input clk,
input rstn,
output reg done
);
// 状态声明
localparam [1:0] S_IDLE = 2'b00, S_START = 2'b01, S_DONE = 2'b10;
// 状态寄存器
reg [1:0] current_state, next_state;
// 状态转换逻辑
always @(posedge clk or posedge reset) begin
if (!rstn) begin
done = 0;
current_state <= S_IDLE;
end
else begin
current_state <= next_state;
end
end
// 下一个状态和输出逻辑
always @(*) begin
case (current_state)
S_IDLE: begin
if (start) begin
next_state = S_START;
end
end
S_START: begin
// 执行一些操作...
next_state = S_DONE;
end
S_DONE: begin
done = 1'b1;
next_state = S_IDLE;
end
default:
next_state = S_IDLE;
endcase
end
endmodule
此外,还需要注意以下几点:
- 开始状态,这个状态通常都是做一些信号的初始化,然后再执行下一个状态;
- 结束状态,也就是最后一个状态,这时需要回到最开始的状态;
- default 的情况,通常都是回到开始状态。
SystemVerilog中的测试平台
以下是上述状态机的SystemVerilog测试平台(testbench)代码示例:
module tb_moore_state_machine;
// 测试平台信号
reg clk, reset, done;
// 实例化状态机模块
moore_state_machine uut(
.clk(clk),
.reset(reset),
.done(done)
);
// 时钟生成
always #5 clk = ~clk;
// 测试序列
initial begin
// 初始化信号
clk = 0;
rstn = 0;
#10;
// 释放复位
reset = 1;
#30;
// 断言检查状态机是否正确完成
assert (done === 1'b1) else $error("状态机未正确完成。");
// 仿真结束
$finish;
end
endmodule
VCS 波形仿真

所以可以看出来仿真结果并不是预期中的,这里主要是由于什么问题导致的?答案是阻塞赋值与非阻塞赋值,接下来对它进行详细介绍。
阻塞赋值和非阻塞赋值
在 always 语句块中, Verilog 语言支持两种类型的赋值: 阻塞赋值和非阻塞赋值。 阻塞赋值使用
“=” 语句; 非阻塞赋值使用“<=” 语句。
阻塞赋值: 在一个“begin…end” 的多行赋值语句, 先执行当前行的赋值语句, 再执行下一行的赋值语句。
非阻塞赋值: 在一个“begin…end” 的多行赋值语句, 在同一时间内同时赋值。
begin
c = a;
d = c + a;
end
begin
c <= a;
d <= c + a;
end
上面两个例子中, 第1个例子是阻塞赋值, 程序会先执行第 1 行, 得到结果后再执行第 2 行。第2个例子是非阻塞赋值, 两行的赋值语句是同时执行的。
组合逻辑中应使用阻塞赋值“=” , 时序逻辑中应使用非阻塞赋值“<=” 。 可以将这个规则牢牢记住, 按照这一规则进行设计绝对不会发生错误。
对代码做了如下两处修改(将阻塞赋值修改wield非阻塞赋值,同时检测任意信号变化):

仿真波形图如下:
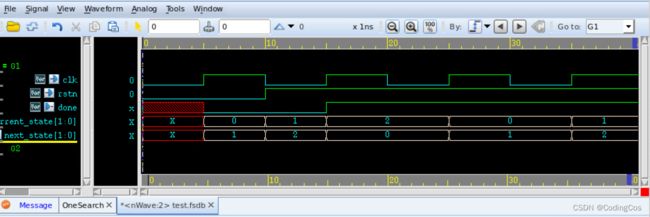
如果再将 “下一个状态和输出逻辑” 中的 always @(*) begin 修改为always @(posedge clk or posedge reset) begin 之后则会出现仿真失败,波形图如下:
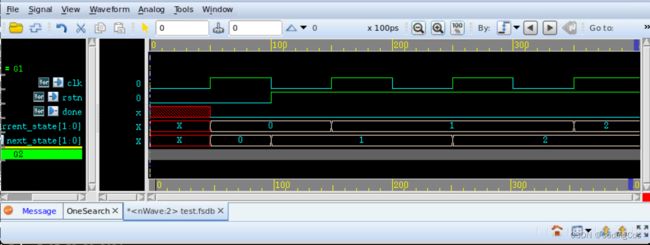
不太清楚是什么原因导致的这个问题!!!
有限状态机(FSM)与无限状态机的区别
有限状态机(FSM):
- 有限状态机具有一个定义良好的状态集,这个集合是有限的。
- 通常包括状态、转换、输入和(可选的)输出。
- FSM可以是确定性的(每个状态和输入组合对应一个唯一的后继状态)也可以是非确定性的(一个状态和输入组合可以对应多个后继状态)。
- FSM广泛用于硬件设计、协议实现、解析器和其他工程应用。
无限状态机:
- 理论上,无限状态机拥有无限多个状态,但这在实际硬件设计中不是可行的,因为硬件资源是有限的。
- 在软件中,无限状态机可能通过数据结构和不断变化的状态信息来模拟无限状态的概念。
- 无限状态机通常是指在概念模型中可能具有无限状态的系统,如某些类型的自动机或计算模型。
在实际硬件设计中,我们通常处理的是有限状态机。无限状态机更多地是计算理论的一部分,用于研究计算能力和复杂性等问题。