Java如何对二叉树双亲表示发存储_C语言数据结构树的双亲表示法实例详解
1、树的双亲表示法:
树的双亲表示法
2、/* bo6-4.c 树的双亲表存储(存储结构由c6-4.h定义)的基本操作(14个) */
Status InitTree(PTree *T)
{ /* 操作结果: 构造空树T */
(*T).n=0;
return OK;
}
void DestroyTree()
{ /* 由于PTree是定长类型,无法销毁 */
}
typedef struct
{
int num;
TElemType name;
}QElemType; /* 定义队列元素类型 */
#include"c3-2.h" /* 定义LinkQueue类型 */
#include"bo3-2.c" /* LinkQueue类型的基本操作 */
Status CreateTree(PTree *T)
{ /* 操作结果: 构造树T */
LinkQueue q;
QElemType p,qq;
int i=1,j,l;
char c[MAX_TREE_SIZE]; /* 临时存放孩子结点数组 */
InitQueue(&q); /* 初始化队列 */
printf("请输入根结点(字符型,空格为空): ");
scanf("%c%*c",&(*T).nodes[0].data); /* 根结点序号为0,%*c吃掉回车符 */
if((*T).nodes[0].data!=Nil) /* 非空树 */
{
(*T).nodes[0].parent=-1; /* 根结点无双亲 */
qq.name=(*T).nodes[0].data;
qq.num=0;
EnQueue(&q,qq); /* 入队此结点 */
while(i
{
DeQueue(&q,&qq); /* 出队一个结点 */
printf("请按长幼顺序输入结点%c的所有孩子: ",qq.name);
gets(c);
l=strlen(c);
for(j=0;j
{
(*T).nodes[i].data=c[j];
(*T).nodes[i].parent=qq.num;
p.name=c[j];
p.num=i;
EnQueue(&q,p); /* 入队此结点 */
i++;
}
}
if(i>MAX_TREE_SIZE)
{
printf("结点数超过数组容量\n");
exit(OVERFLOW);
}
(*T).n=i;
}
else
(*T).n=0;
return OK;
}
#define ClearTree InitTree /* 二者操作相同 */
Status TreeEmpty(PTree T)
{ /* 初始条件: 树T存在。操作结果: 若T为空树,则返回TRUE,否则返回FALSE */
if(T.n)
return FALSE;
else
return TRUE;
}
int TreeDepth(PTree T)
{ /* 初始条件: 树T存在。操作结果: 返回T的深度 */
int k,m,def,max=0;
for(k=0;k
{
def=1; /* 初始化本际点的深度 */
m=T.nodes[k].parent;
while(m!=-1)
{
m=T.nodes[m].parent;
def++;
}
if(max
max=def;
}
return max; /* 最大深度 */
}
TElemType Root(PTree T)
{ /* 初始条件: 树T存在。操作结果: 返回T的根 */
int i;
for(i=0;i
if(T.nodes[i].parent<0)
return T.nodes[i].data;
return Nil;
}
TElemType Value(PTree T,int i)
{ /* 初始条件: 树T存在,i是树T中结点的序号。操作结果: 返回第i个结点的值 */
if(i
return T.nodes[i].data;
else
return Nil;
}
Status Assign(PTree *T,TElemType cur_e,TElemType value)
{ /* 初始条件: 树T存在,cur_e是树T中结点的值。操作结果: 改cur_e为value */
int j;
for(j=0;j
{
if((*T).nodes[j].data==cur_e)
{
(*T).nodes[j].data=value;
return OK;
}
}
return ERROR;
}
TElemType Parent(PTree T,TElemType cur_e)
{ /* 初始条件: 树T存在,cur_e是T中某个结点 */
/* 操作结果: 若cur_e是T的非根结点,则返回它的双亲,否则函数值为"空" */
int j;
for(j=1;j
if(T.nodes[j].data==cur_e)
return T.nodes[T.nodes[j].parent].data;
return Nil;
}
TElemType LeftChild(PTree T,TElemType cur_e)
{ /* 初始条件: 树T存在,cur_e是T中某个结点 */
/* 操作结果: 若cur_e是T的非叶子结点,则返回它的最左孩子,否则返回"空" */
int i,j;
for(i=0;i
if(T.nodes[i].data==cur_e) /* 找到cur_e,其序号为i */
break;
for(j=i+1;j
if(T.nodes[j].parent==i) /* 根据树的构造函数,最左孩子(长子)的序号<其它孩子的序号 */
return T.nodes[j].data;
return Nil;
}
TElemType RightSibling(PTree T,TElemType cur_e)
{ /* 初始条件: 树T存在,cur_e是T中某个结点 */
/* 操作结果: 若cur_e有右(下一个)兄弟,则返回它的右兄弟,否则返回"空" */
int i;
for(i=0;i
if(T.nodes[i].data==cur_e) /* 找到cur_e,其序号为i */
break;
if(T.nodes[i+1].parent==T.nodes[i].parent)
/* 根据树的构造函数,若cur_e有右兄弟的话则右兄弟紧接其后 */
return T.nodes[i+1].data;
return Nil;
}
Status Print(PTree T)
{ /* 输出树T。加 */
int i;
printf("结点个数=%d\n",T.n);
printf(" 结点 双亲\n");
for(i=0;i
{
printf(" %c",Value(T,i)); /* 结点 */
if(T.nodes[i].parent>=0) /* 有双亲 */
printf(" %c",Value(T,T.nodes[i].parent)); /* 双亲 */
printf("\n");
}
return OK;
}
Status InsertChild(PTree *T,TElemType p,int i,PTree c)
{ /* 初始条件: 树T存在,p是T中某个结点,1≤i≤p所指结点的度+1,非空树c与T不相交 */
/* 操作结果: 插入c为T中p结点的第i棵子树 */
int j,k,l,f=1,n=0; /* 设交换标志f的初值为1,p的孩子数n的初值为0 */
PTNode t;
if(!TreeEmpty(*T)) /* T不空 */
{
for(j=0;j
if((*T).nodes[j].data==p) /* p的序号为j */
break;
l=j+1; /* 如果c是p的第1棵子树,则插在j+1处 */
if(i>1) /* c不是p的第1棵子树 */
{
for(k=j+1;k
if((*T).nodes[k].parent==j) /* 当前结点是p的孩子 */
{
n++; /* 孩子数加1 */
if(n==i-1) /* 找到p的第i-1个孩子,其序号为k1 */
break;
}
l=k+1; /* c插在k+1处 */
} /* p的序号为j,c插在l处 */
if(l
for(k=(*T).n-1;k>=l;k--) /* 依次将序号l以后的结点向后移c.n个位置 */
{
(*T).nodes[k+c.n]=(*T).nodes[k];
if((*T).nodes[k].parent>=l)
(*T).nodes[k+c.n].parent+=c.n;
}
for(k=0;k
{
(*T).nodes[l+k].data=c.nodes[k].data; /* 依次将树c的所有结点插于此处 */
(*T).nodes[l+k].parent=c.nodes[k].parent+l;
}
(*T).nodes[l].parent=j; /* 树c的根结点的双亲为p */
(*T).n+=c.n; /* 树T的结点数加c.n个 */
while(f)
{ /* 从插入点之后,将结点仍按层序排列 */
f=0; /* 交换标志置0 */
for(j=l;j
if((*T).nodes[j].parent>(*T).nodes[j+1].parent)
{/* 如果结点j的双亲排在结点j+1的双亲之后(树没有按层序排列),交换两结点*/
t=(*T).nodes[j];
(*T).nodes[j]=(*T).nodes[j+1];
(*T).nodes[j+1]=t;
f=1; /* 交换标志置1 */
for(k=j;k
if((*T).nodes[k].parent==j)
(*T).nodes[k].parent++; /* 双亲序号改为j+1 */
else if((*T).nodes[k].parent==j+1)
(*T).nodes[k].parent--; /* 双亲序号改为j */
}
}
return OK;
}
else /* 树T不存在 */
return ERROR;
}
Status deleted[MAX_TREE_SIZE+1]; /* 删除标志数组(全局量) */
void DeleteChild(PTree *T,TElemType p,int i)
{ /* 初始条件: 树T存在,p是T中某个结点,1≤i≤p所指结点的度 */
/* 操作结果: 删除T中结点p的第i棵子树 */
int j,k,n=0;
LinkQueue q;
QElemType pq,qq;
for(j=0;j<=(*T).n;j++)
deleted[j]=0; /* 置初值为0(不删除标记) */
pq.name='a'; /* 此成员不用 */
InitQueue(&q); /* 初始化队列 */
for(j=0;j
if((*T).nodes[j].data==p)
break; /* j为结点p的序号 */
for(k=j+1;k
{
if((*T).nodes[k].parent==j)
n++;
if(n==i)
break; /* k为p的第i棵子树结点的序号 */
}
if(k
{
n=0;
pq.num=k;
deleted[k]=1; /* 置删除标记 */
n++;
EnQueue(&q,pq);
while(!QueueEmpty(q))
{
DeQueue(&q,&qq);
for(j=qq.num+1;j
if((*T).nodes[j].parent==qq.num)
{
pq.num=j;
deleted[j]=1; /* 置删除标记 */
n++;
EnQueue(&q,pq);
}
}
for(j=0;j
if(deleted[j]==1)
{
for(k=j+1;k<=(*T).n;k++)
{
deleted[k-1]=deleted[k];
(*T).nodes[k-1]=(*T).nodes[k];
if((*T).nodes[k].parent>j)
(*T).nodes[k-1].parent--;
}
j--;
}
(*T).n-=n; /* n为待删除结点数 */
}
}
void TraverseTree(PTree T,void(*Visit)(TElemType))
{ /* 初始条件:二叉树T存在,Visit是对结点操作的应用函数 */
/* 操作结果:层序遍历树T,对每个结点调用函数Visit一次且仅一次 */
int i;
for(i=0;i
Visit(T.nodes[i].data);
printf("\n");
}
3、/* c6-4.h 树的双亲表存储表示 */
#define MAX_TREE_SIZE 100
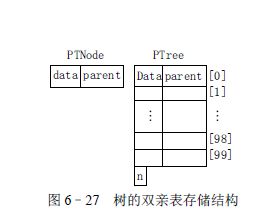
typedef struct
{
TElemType data;
int parent; /* 双亲位置域 */
} PTNode;
typedef struct
{
PTNode nodes[MAX_TREE_SIZE];
int n; /* 结点数 */
} PTree
4、/* main6-4.c 检验bo6-4.c的主程序 */
typedef char TElemType;
TElemType Nil=' '; /* 以空格符为空 */
#include"c6-4.h"
#include"bo6-4.c"
void vi(TElemType c)
{
printf("%c ",c);
}
void main()
{
int i;
PTree T,p;
TElemType e,e1;
InitTree(&T);
printf("构造空树后,树空否? %d(1:是 0:否) 树根为%c 树的深度为%d\n",TreeEmpty(T),Root(T),TreeDepth(T));
CreateTree(&T);
printf("构造树T后,树空否? %d(1:是 0:否) 树根为%c 树的深度为%d\n",TreeEmpty(T),Root(T),TreeDepth(T));
printf("层序遍历树T:\n");
TraverseTree(T,vi);
printf("请输入待修改的结点的值 新值: ");
scanf("%c%*c%c%*c",&e,&e1);
Assign(&T,e,e1);
printf("层序遍历修改后的树T:\n");
TraverseTree(T,vi);
printf("%c的双亲是%c,长子是%c,下一个兄弟是%c\n",e1,Parent(T,e1),LeftChild(T,e1),RightSibling(T,e1));
printf("建立树p:\n");
InitTree(&p);
CreateTree(&p);
printf("层序遍历树p:\n");
TraverseTree(p,vi);
printf("将树p插到树T中,请输入T中p的双亲结点 子树序号: ");
scanf("%c%d%*c",&e,&i);
InsertChild(&T,e,i,p);
Print(T);
printf("删除树T中结点e的第i棵子树,请输入e i: ");
scanf("%c%d",&e,&i);
DeleteChild(&T,e,i);
Print(T);
}
感谢阅读,希望能帮助到大家,谢谢大家对本站的支持!