数据探索与可视化:异常值

目录

一.导读

二.介绍

①对于单个变量的异常值的查找

 Ⅰ.代码处理分析

Ⅱ.可视化

补充：四分位数 

1.定义：

2.位置的确定

②对于多个变量的异常值的查找

三.结尾

---

一.导读

本篇我们进入到数据分析中经常能遇到的异常值问题，当然对于异常值的发现自然也是少不了对数据进行可视化。

二.介绍

①对于单个变量的异常值的查找

 Ⅰ.代码处理分析

from sklearn.impute import KNNImputer
import matplotlib.pyplot as plt
import pandas as pd
naindex=pd.isna(ocean_data.AirTemp)|pd.isna(ocean_data.Humidity)
ocean_data=pd.read_csv(r'C:\Users\asuspc\Desktop\program\data\chap2\热带大气海洋数据.csv')
knnimp=KNNImputer(n_neighbors=5)
ocean_data_knn=knnimp.fit_transform(ocean_data)

我们先读取数据，利用先前已经通过K-近邻插补法进行插补的数据进行各个数据项的异常值查找。利用sklearn.impute的KNNImputer方法对原始数据进行处理。

ocean_data_knn2=pd.DataFrame(data=ocean_data_knn[:,3:8],columns=["SeaSurfaceTemp","AirTemp","Humidity","UWind","VWind"])

我们通过pandas的dataframe的方法将我们去除了年份、经度和维度的数据表放入新建的数据表中并存放到新的变量当中，columns是设置列的数据项。

ocean_data_knn2_mean=ocean_data_knn2.mean()
ocean_data_knn2_std=ocean_data_knn2.std()
outliers=abs(ocean_data_knn2 - ocean_data_knn2_mean)>3*ocean_data_knn2_std

算出对应数据的均值和标准差(对应的是mean和std方法)之后，就可以开始寻找异常值，二异常值的原则如下：

3δ原则：当数据服从正态分布时，数据出现在三个标准差范围内的概率是99.7%，因此不满足3δ原则的数据认定为异常值。

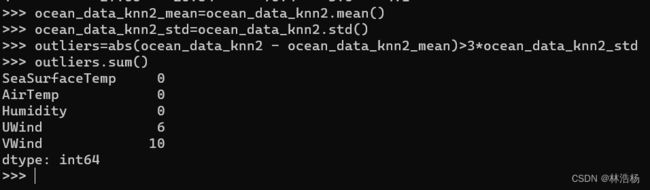
于是有了第三条代码的关系式，运用sum方法我们得出了各个数据项的异常值：

那么各个数据项存在的异常值的个数信息就生成出来了。

Ⅱ.可视化

然而针对这个数据我们也能通过箱线图进行可视化：

ocean_data_knn2.plot(kind='box',figsize=(10,6))
plt.title('Box-plot')
plt.grid()
plt.show()

在plot方法当中使用kind参数对要使用的图形进行设置，并对图形窗口大小进行设置。 

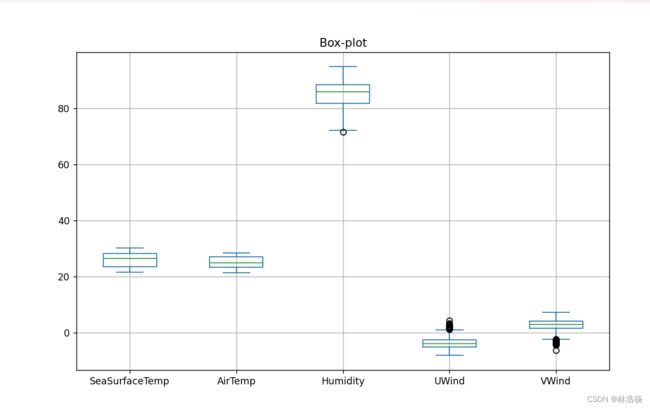
那么画出箱线图之后，我们来看看以下图是如何解释箱线图：

可以看出在上下边缘之外的标记点则就是异常值，回到我们自己画出的图中可以发现:Humidity有一个异常值，而Uwind和Vwind则有多个异常值

图中也同时标出了均值、中位数的代表记号，而上下四分位数是什么呢？若有兴趣花点时间可看看如下的补充点。

补充：四分位数 

1.定义：

四分位数（Quartile）是统计学中分位数的一种，即把所有数据由小到大排列并分成四等份，处于三个分割点位置的数据就是四分位数。

2.位置的确定

第一四分位数 (Q1)，又称“下四分位数”，等于该样本中所有数据由小到大排列后第25%的数据； 第二四分位数 (Q2)，又称“中位数”，等于该样本中所有数据由小到大排列后第50%数据；                第三四分位数 (Q3)，又称“上四分位数”，等于该样本中所有数据由小到大排列后第75%的数据；    注意：第三四分位数与第一四分位数的差距又称四分位距（InterQuartile Range, IQR）。

②对于多个变量的异常值的查找

x=[10,8,13,9,11,14,6,4,12,7,5]
y=[7.46,6.77,12.74,7.11,7.81,8.84,6.08,5.39,8.15,6.42,5.73]
plt.figure(figsize=(10,6))
plt.scatter(x,y,c='blue',marker='o')
plt.grid()
plt.xlabel("X")
plt.ylabel("Y")
plt.text(12.5,12,'Outliers')
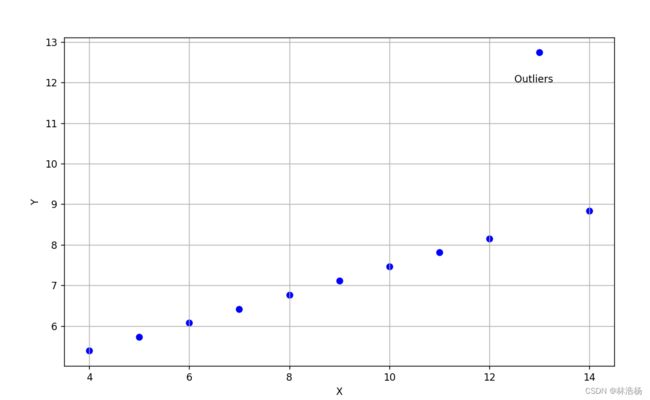
plt.show()

这里我们补充一个画图的知识点，通过text方法我们能够给出具体的点位标记处对某点进行文本标记。 

可以看出异常点是与其他点明显有着不同的趋势，这也为我们提供了一种寻找异常点的好方法，通过散点图我们能看出数据的分布情况，进而看出数据的分布趋势，那么很显然，不符合趋势的就是我们要找的异常值。 

三.结尾

 通过数据异常值的发现之后，我们开始进入数据可视化的部分，加强构图与分析/处理数据的能力。