【Py/Java/C++三种语言OD2023C卷真题】20天拿下华为OD笔试之【模拟】2023C-灰度图恢复【欧弟算法】全网注释最详细分类最全的华为OD真题题解

题目描述与示例

题目描述

黑白图像常采用灰度图的方式存储，即图像的每像素填充一个灰阶值，256阶灰度图是个灰阶值取值范围为0-255的灰阶矩阵，0表示全黑，255表示全白，范围内的其他值表示不同的灰度，比如下面的图像及其对应的灰阶矩阵:

但在计算机中实际存储时，会使用压缩算法，其中一种压缩格式和描述如下：10 10 255 34 0 1 255 8 0 3 255 6 0 5 255 4 0 7 255 2 0 9 255 21

1. 有数值以空格分隔
2. 前两个数分别表示矩阵的行数和列数
3. 从第三个数开始，每两个数一组，每组第一个数是灰阶值，第二个数表示该灰阶值以左到右，从上到下（可理解为将二维数组按行存储在一维矩阵中)的连续像素个数。比如题目所述例子，255 34表示有连续34个像素的灰阶值是255。如此，图像软件在打开此格式灰度图的时候，就可以根据此算法从压缩数据恢复出原始灰度图矩阵。

请从输入的压缩数恢复灰度图原始矩阵，并返回指定像素的灰阶值。

输入描述

输入包括两行，第一行是灰度图压缩数据，第二行表示一个像素位置的行号和列号，如 0 0 表示左上角像素

输出描述

一个数字，表示输入数据表示的灰阶矩阵的指定像素的灰阶值

补充说明

1. 系统保证输入的压缩数据是合法有效的，不会出现数据越界、数值不合法等无法恢复的场景
2. 系统保证输入的像素坐标是合法的，不会出现不在矩阵中的像素
3. 矩阵的行和列数范围为: (0, 100]
4. 灰阶值取值范围为 [0,255]

示例一

输入

10 10 255 34 0 1 255 8 0 3 255 6 0 5 255 4 0 7 255 2 0 9 255 21
3 4

输出

0

示例二

输入

10 10 56 34 99 1 87 8 99 3 255 6 99 5 255 4 99 7 255 2 99 9 255 21 
3 4

输出

99

解题思路

在确保理解题意的前提下，本题属于要求比较明确的模拟题。

一种很容易想到的做法是，构建一个n*m的二维矩阵mat，按照压缩格式直接将灰度图恢复出来，再取出给定的坐标(r, c)的值即可。由于这种做法比较简单直接，其空间复杂度为O(nm)，故略去不表。

以下讨论一种空间复杂度为O(1)的方法。

二维索引的一维索引映射

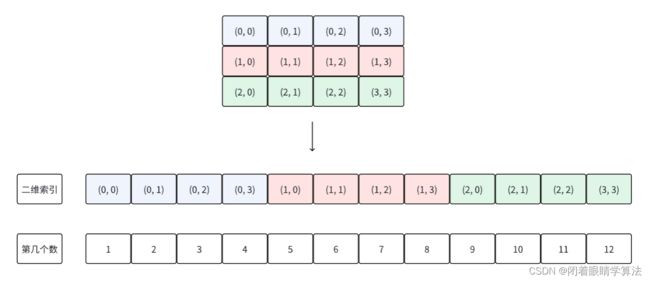
对于大小n*m的矩阵而言，其左上角的索引为(0, 0)，右下角的索引为(n-1, m-1)。如果我们把整个二维矩阵根据行展开成一个一维数组，譬如对于一个3*4的二维矩阵做如下图所示的展开

假设某个位置的二维索引为(i, j)，那么其对应的一维索引idx = i*m+j。即一维索引的值为二维索引的行索引乘以每行元素的个数（列数）加上列索引。

因此我们可以得到二维索引的一维索引映射。

为什么需要一维索引映射

使用一维索引映射的目的是显而易见的，因为题目所给的灰度压缩格式是跨行的，即可能存在连续的若干个同值灰度，它们在实际的二维矩阵中并不位于同一行。

由于题目只要求计算点(r, c)的灰度值，所以不妨直接将压缩格式看成是一个一维数组来进行判断。

如何确定所给点的灰度

由于压缩算法所包含的信息是连续的同值灰度点的个数，因此计数是从1开始的。如下图所示

因此不妨直接定义idx = i*m+j+1，表示所给定点在展开的一维数组中是第几个数，其中+1表示计数是从1而不是从0开始的。然后遍历所有的连续灰度段(val, num)，其中val为该连续灰度段的灰度值，num为该段连续灰度值的点的个数，并且维护一个变量total_num来表示当前已经考虑了多少个灰度值（考虑了多少个数）：

• 将当前连续灰度段的个数num计入total_num中，即total_num += num。若
  • total_num < idx，说明还没到达第idx个数，继续遍历
  • total_num >= idx，说明已经到达了第idx个数，total_num-num < idx <= total_num，此时一维数组中的第idx个数必然位于该连续灰度段中，因此第idx个数的灰度值为val，即原来在二维矩阵中的点(r, c)的灰度值为val

代码

Python

# 题目：【模拟】2023C-灰度图恢复
# 分值：100
# 作者：许老师-闭着眼睛学数理化
# 算法：模拟
# 代码看不懂的地方，请直接在群上提问


# 输入第一行数据
lst = list(map(int, input().split()))
# 第一行数据中的前两个位置，为二维矩阵的大小n和m
n, m = lst[0], lst[1]
# 第一行数据中的剩余位置，为灰度压缩数据
nums = lst[2:]
# 注意：如果使用解包方法来读取第一行数据，可以写为
# n, m, *nums = list(map(int, input().split()))
# 和上述三行的作用是一致的

# 输入第二行数据，要求查询的点的二维索引
r, c = map(int, input().split())

# 计算点(r, c)在一维数组中是第几个数
# 注意此处需要+1，表示计数是从1开始的
idx = r*m+c+1

# 获得压缩数据的长度，一共为k//2组数据
k = len(nums)
# 当前已经考虑的灰度值个数，初始化为0
total_num = 0
# 每两个一组遍历数据
for i in range(0, k, 2):
    # 分别获得当前压缩灰度段的值val和个数num
    val, num = nums[i], nums[i+1]
    # 将当前压缩灰度段的个数num计入total_num中
    total_num += num
    # 如果total大于等于idx，说明第idx个数位于当前灰度段中
    # 输入val，并且退出循环
    if total_num >= idx:
        print(val)
        break

Java

import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        
        String[] input = scanner.nextLine().split(" ");
        int n = Integer.parseInt(input[0]);
        int m = Integer.parseInt(input[1]);
        int[] nums = new int[input.length - 2];
        
        for (int i = 2; i < input.length; i++) {
            nums[i - 2] = Integer.parseInt(input[i]);
        }

        int r = scanner.nextInt();
        int c = scanner.nextInt();
        int idx = r * m + c + 1;

        int totalNum = 0;

        for (int i = 0; i < nums.length; i += 2) {
            int val = nums[i];
            int num = nums[i + 1];
            totalNum += num;

            if (totalNum >= idx) {
                System.out.println(val);
                break;
            }
        }
    }
}

C++

#include 
#include 
#include 

int main() {
    std::string line;
    std::getline(std::cin, line);
    std::istringstream iss(line);

    int n, m;
    iss >> n >> m;

    std::vector<int> nums;
    int num;
    while (iss >> num) {
        nums.push_back(num);
    }

    int r, c;
    std::cin >> r >> c;
    int idx = r * m + c + 1;

    int totalNum = 0;

    for (int i = 0; i < nums.size(); i += 2) {
        int val = nums[i];
        int num = nums[i + 1];
        totalNum += num;

        if (totalNum >= idx) {
            std::cout << val << std::endl;
            break;
        }
    }

    return 0;
}

时空复杂度

时间复杂度：O(k)。需要遍历k组数据。

空间复杂度：O(1)。无需构建二维矩阵，仅需若干常数变量。

---

华为OD算法/大厂面试高频题算法练习冲刺训练

• 华为OD算法/大厂面试高频题算法冲刺训练目前开始常态化报名！目前已服务100+同学成功上岸！

• 课程讲师为全网50w+粉丝编程博主@吴师兄学算法 以及小红书头部编程博主@闭着眼睛学数理化

• 每期人数维持在20人内，保证能够最大限度地满足到每一个同学的需求，达到和1v1同样的学习效果！

• 60+天陪伴式学习，40+直播课时，300+动画图解视频，300+LeetCode经典题，200+华为OD真题/大厂真题，还有简历修改、模拟面试、专属HR对接将为你解锁

• 可上全网独家的欧弟OJ系统练习华子OD、大厂真题

• 可查看链接 大厂真题汇总 & OD真题汇总(持续更新)

• 绿色聊天软件戳 od1336了解更多