代码随想录day13--二叉树的应用1

LeetCode102.二叉树的层序遍历

题目描述：

给你二叉树的根节点 root ，返回其节点值的 层序遍历 。 （即逐层地，从左到右访问所有节点）。

示例 1：

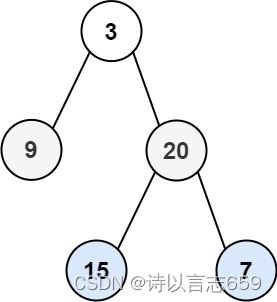
输入：root = [3,9,20,null,null,15,7]
输出：[[3],[9,20],[15,7]]

示例 2：

输入：root = [1]
输出：[[1]]

示例 3：

输入：root = []
输出：[]

解题思路：

·二叉树的层序遍历，可以理解为图的广度遍历，一层一层的向下遍历。所以我们之前学习过的三种遍历方式都无法使用了，因为之前学习的三种遍历方法相当于是深度遍历。

·我们在解这道题可以使用队列进行辅助，因为输出形式为二维数组，所以我们需要使用二维数组进行求解。

·我们先将一层的结点放入队列中，然后使用一个变量size记录下此时的队列长度（一定要记录因为队列长度是会改变的），再遍历看这个结点是否有左右孩子，如果有就放入队列中，如果没有就结束遍历，再将size中的数值取出，当size==0后，再重新记录队列的长度。直到size的值为0且不再改变后结束遍历。

代码如下：

class Solution {
public:
    vector> levelOrder(TreeNode* root) {
        queue que;
        if(root != NULL) que.push(root);
        vector> result;
        while(que.size() != 0){
            int size = que.size();
            vector vec;
            for(int i = 0;i < size;i++){//这里一定要使用size，如果使用que.size则会混乱
                TreeNode* node = que.front();
                que.pop();
                vec.push_back(node->val);
                if(node->left) que.push(node->left);
                if(node->right) que.push(node->right);
            }
            result.push_back(vec);
        }
        return result;
    }
};

·时间复杂度:O(n)

·空间复杂度:O(n)

难点：

·使用队列，可能无法想到使用

·循环遍历中的size一定不能使用成que.size()

总结：写题目需要和之前学过的知识融会贯通，这样才能正确的求解，这是一道非常经典的题目。

LeetCode226.翻转二叉树

题目描述：

给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

示例 1：

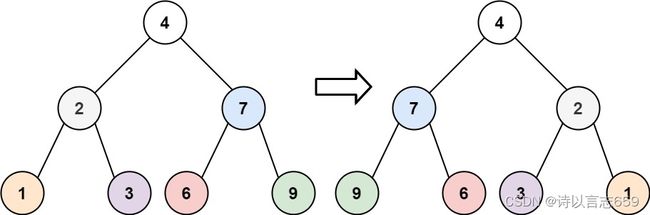
输入：root = [4,2,7,1,3,6,9]
输出：[4,7,2,9,6,3,1]

示例 2：

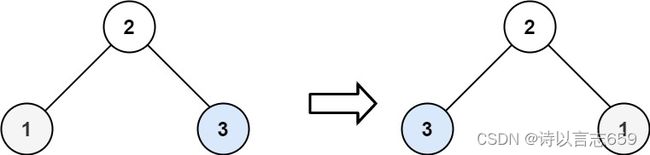
输入：root = [2,1,3]
输出：[2,3,1]

示例 3：

输入：root = []
输出：[]

解题思路：

·看到题目后不要被题目吓到，这道题其实没有想象中那么难，我们只需要找到准确的解题方法就可以轻松解开。这道题并不是将数值进行调换，而是对指针进行操作，所以我们就可以一层一层的将每个结点的左右孩子进行交互，从而解题。

代码如下：

class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        queue que;
        if(root != NULL) que.push(root);
        while(!que.empty()){
            int size = que.size();
            for(int i = 0;i < size;i++){
                TreeNode* node = que.front();
                que.pop();
                swap(node->left,node->right);//注意swap位置不能写错，只能写在left和right前或者后
                if(node->left) que.push(node->left);
                if(node->right) que.push(node->right);
            }
        }
        return root;
    }
};

易错点：

·会有同学认为一定要从下向上交换左右孩子，这样才能正确解开，但是题目说的是交换指针，并非交换数值，所以可以层层遍历

·swap函数的位置，可以写在left、right前或后，但是不能写在中间，写在中间可以正确解题，但是会多很多步骤，得不偿失

总结：这道题可以使用先序遍历或后续遍历再利用swap函数进行求解，但是由于前一题是层次遍历，所以选择使用层次遍历进行求解，其代码也未改变多少。

LeetCode101.对称二叉树

题目描述：

给你一个二叉树的根节点 root ， 检查它是否轴对称。

示例 1：

输入：root = [1,2,2,3,4,4,3]
输出：true

示例 2：

输入：root = [1,2,2,null,3,null,3]
输出：false

解题思路：

·这道题要比较的并不是左右，而是对称的结点，在遍历时，也需要仔细思考清楚。

·这道题所使用的是后序遍历，也一定是后序遍历，因为我们要通过递归函数的返回值，来判断两个子树的内测节点和外侧节点是否相等。正是因为要遍历两棵树而去要比较内侧和外侧节点，所以准确的来说是一个树的顺序遍历是左右中，一个树的遍历顺序是右左中。

·如何判断节点值是否相等，不需要很复杂，只用&&运算即可

代码如下：

class Solution {
public:
    bool compare(TreeNode* left,TreeNode* right){
        if(left == NULL && right != NULL) return false;
        else if(left != NULL && right == NULL) return false;
        else if(left == NULL && right == NULL) return true;//以后均为排除空节点
        else if(left->val != right->val) return false;//排除数值不同
        
        //左右节点都不为空，且数值相同
        bool outside = compare(left->left,right->right);//左子树：左，右子树：右
        bool inside = compare(left->right,right->left);//左子树：右，右子树：左
        bool inSame = outside&& inside;//判断结点是否相同
        return inSame;
    }
    bool isSymmetric(TreeNode* root) {
        if(root == NULL) return true;
        return compare(root->left,root->right);
    }
};

易错点：

·判断空结点失误

·递归针对的结点失误

·需要判断是否相等的节点错误

总结：这道题看代码十分的简洁，但是递归三部曲并没有很好的体现出来，大家在做题的时候，要想清楚逻辑，把所有的情况都想到位。尤其是递归的时候，要按照代码随想录day10的递归方法进行求解。