【深蓝学院】移动机器人运动规划--第2章 基于搜索的路径规划--作业

1. Assignment

先上A* 代码：

#include "Astar_searcher.h"

using namespace std;
using namespace Eigen;

//初始化grid map
void AstarPathFinder::initGridMap(double _resolution, Vector3d global_xyz_l, Vector3d global_xyz_u, int max_x_id, int max_y_id, int max_z_id)
{   
    gl_xl = global_xyz_l(0);//这个应该是左下边界
    gl_yl = global_xyz_l(1);
    gl_zl = global_xyz_l(2);

    gl_xu = global_xyz_u(0);
    gl_yu = global_xyz_u(1);
    gl_zu = global_xyz_u(2);
    
    GLX_SIZE = max_x_id;
    GLY_SIZE = max_y_id;
    GLZ_SIZE = max_z_id;
    GLYZ_SIZE  = GLY_SIZE * GLZ_SIZE;
    GLXYZ_SIZE = GLX_SIZE * GLYZ_SIZE;//计算出整个map的最大index

    resolution = _resolution;
    inv_resolution = 1.0 / _resolution;    

    data = new uint8_t[GLXYZ_SIZE];
    memset(data, 0, GLXYZ_SIZE * sizeof(uint8_t));

    //二重指针数组，这样理解：
    // int[5]是一个一维数组元素是int数，是一条线，
    // int*[5]是一个二维数组，元素是一维数组指针，首地址是第1条线的地址，+1访问下一条线，
    // int**[5]是3维数组，元素是2维数组指针，是一个矩形空间，首地址是第一个平面的地址，+1访问下一个平面
    GridNodeMap = new GridNodePtr ** [GLX_SIZE];//存放所有grid node 的数组
    for(int i = 0; i < GLX_SIZE; i++){
        GridNodeMap[i] = new GridNodePtr * [GLY_SIZE];
        for(int j = 0; j < GLY_SIZE; j++){
            GridNodeMap[i][j] = new GridNodePtr [GLZ_SIZE];
            for( int k = 0; k < GLZ_SIZE;k++){
                Vector3i tmpIdx(i,j,k);
                Vector3d pos = gridIndex2coord(tmpIdx);
                GridNodeMap[i][j][k] = new GridNode(tmpIdx, pos);
            }
        }
    }
    ROS_DEBUG("\nheuristic: %d, tie breaker: %d", heu_, tie_breaker_);
}

void AstarPathFinder::resetGrid(GridNodePtr ptr)
{
    ptr->id = 0;
    ptr->cameFrom = NULL;
    ptr->gScore = inf;
    ptr->fScore = inf;
}

void AstarPathFinder::resetUsedGrids()
{   
    for(int i=0; i < GLX_SIZE ; i++)
        for(int j=0; j < GLY_SIZE ; j++)
            for(int k=0; k < GLZ_SIZE ; k++)
                resetGrid(GridNodeMap[i][j][k]);
}

void AstarPathFinder::setObs(const double coord_x, const double coord_y, const double coord_z)
{
    if( coord_x < gl_xl  || coord_y < gl_yl  || coord_z <  gl_zl || 
        coord_x >= gl_xu || coord_y >= gl_yu || coord_z >= gl_zu )
        return;

    int idx_x = static_cast<int>( (coord_x - gl_xl) * inv_resolution);
    int idx_y = static_cast<int>( (coord_y - gl_yl) * inv_resolution);
    int idx_z = static_cast<int>( (coord_z - gl_zl) * inv_resolution);      

    data[idx_x * GLYZ_SIZE + idx_y * GLZ_SIZE + idx_z] = 1;
}

vector<Vector3d> AstarPathFinder::getVisitedNodes()
{   
    vector<Vector3d> visited_nodes;
    for(int i = 0; i < GLX_SIZE; i++)
        for(int j = 0; j < GLY_SIZE; j++)
            for(int k = 0; k < GLZ_SIZE; k++){   
                //if(GridNodeMap[i][j][k]->id != 0) // visualize all nodes in open and close list
                if(GridNodeMap[i][j][k]->id == -1)  // visualize nodes in close list only
                    visited_nodes.push_back(GridNodeMap[i][j][k]->coord);
            }

    ROS_WARN("visited_nodes size : %d", visited_nodes.size());
    return visited_nodes;
}

//idx to coord
Vector3d AstarPathFinder::gridIndex2coord(const Vector3i & index) 
{
    Vector3d pt;

    pt(0) = ((double)index(0) + 0.5) * resolution + gl_xl;
    pt(1) = ((double)index(1) + 0.5) * resolution + gl_yl;
    pt(2) = ((double)index(2) + 0.5) * resolution + gl_zl;

    return pt;
}

Vector3i AstarPathFinder::coord2gridIndex(const Vector3d & pt)
{
    Vector3i idx;
    idx <<  min( max( int( (pt(0) - gl_xl) * inv_resolution), 0), GLX_SIZE - 1),
            min( max( int( (pt(1) - gl_yl) * inv_resolution), 0), GLY_SIZE - 1),
            min( max( int( (pt(2) - gl_zl) * inv_resolution), 0), GLZ_SIZE - 1);

    return idx;
}

Eigen::Vector3d AstarPathFinder::coordRounding(const Eigen::Vector3d & coord)
{
    return gridIndex2coord(coord2gridIndex(coord));
}

inline bool AstarPathFinder::isOccupied(const Eigen::Vector3i & index) const
{
    return isOccupied(index(0), index(1), index(2));
}

inline bool AstarPathFinder::isFree(const Eigen::Vector3i & index) const
{
    return isFree(index(0), index(1), index(2));
}

inline bool AstarPathFinder::isOccupied(const int & idx_x, const int & idx_y, const int & idx_z) const 
{
    return  (idx_x >= 0 && idx_x < GLX_SIZE && idx_y >= 0 && idx_y < GLY_SIZE && idx_z >= 0 && idx_z < GLZ_SIZE && 
            (data[idx_x * GLYZ_SIZE + idx_y * GLZ_SIZE + idx_z] == 1));
}

inline bool AstarPathFinder::isFree(const int & idx_x, const int & idx_y, const int & idx_z) const 
{
    return (idx_x >= 0 && idx_x < GLX_SIZE && idx_y >= 0 && idx_y < GLY_SIZE && idx_z >= 0 && idx_z < GLZ_SIZE && 
           (data[idx_x * GLYZ_SIZE + idx_y * GLZ_SIZE + idx_z] < 1));
}

inline void AstarPathFinder::AstarGetSucc(GridNodePtr currentPtr, vector<GridNodePtr> & neighborPtrSets, vector<double> & edgeCostSets)
{   
    neighborPtrSets.clear();
    edgeCostSets.clear();
    /*
    *
    STEP 4: finish AstarPathFinder::AstarGetSucc yourself 
    please write your code below
    *
    *
    */
    //A*每次找26个neighbor node，判断是否occupied，如果不是，计算edge cost(g)，并加入到open list中
    Eigen::Vector3i tmp_index = currentPtr->index;
    Eigen::Vector3i tmp_lower, tmp_upper;
    tmp_lower <<    min( max( int( (tmp_index(0) - 1) ), 0), GLX_SIZE - 1),
                    min( max( int( (tmp_index(1) - 1) ), 0), GLY_SIZE - 1),
                    min( max( int( (tmp_index(2) - 1) ), 0), GLZ_SIZE - 1);
    tmp_upper <<    min( max( int( (tmp_index(0) + 1) ), 0), GLX_SIZE - 1),
                    min( max( int( (tmp_index(1) + 1) ), 0), GLY_SIZE - 1),
                    min( max( int( (tmp_index(2) + 1) ), 0), GLZ_SIZE - 1);
    for(int i = tmp_lower(0); i <= tmp_upper(0); i++){
        for(int j = tmp_lower(1); j <= tmp_upper(1); j++){
            for(int k = tmp_lower(2); k <= tmp_upper(2); k++){
                //free节点才加入扩展
                Eigen::Vector3i neighbor_idx(i,j,k);
                if(isFree(neighbor_idx) && neighbor_idx != tmp_index) {//只加入free node，且自己不加
                    neighborPtrSets.emplace_back(GridNodeMap[i][j][k]);
                    edgeCostSets.emplace_back(
                            sqrt(
                                std::pow((i - currentPtr->index(0)), 2)
                                + std::pow((j - currentPtr->index(1)), 2)
                                + std::pow((k - currentPtr->index(2)), 2))
                            );
                }
            }
        }
    }
}

double AstarPathFinder::getHeu(GridNodePtr node1, GridNodePtr node2)
{
    /* 
    choose possible heuristic function you want
    Manhattan, Euclidean, Diagonal, or 0 (Dijkstra)
    Remember tie_breaker learned in lecture, add it here ?
    *
    *
    *
    STEP 1: finish the AstarPathFinder::getHeu , which is the heuristic function
    please write your code below
    *
    *
    */
    if(!node1 || !node2) {
        ROS_ERROR("Invalid node pointer");
        return std::numeric_limits<double>::infinity(); // 或其他错误处理方式
    }
    double heuristic_value;
    if( heu_ == ZERO ) {
        return 0;
    } else if ( heu_ == L1 ) {
        heuristic_value = (node1->coord-node2->coord).lpNorm<1>();
    } else if ( heu_ == L2 ) {
        heuristic_value = (node1->coord-node2->coord).lpNorm<2>();
    } else if ( heu_ == DIAGONAL ) {//对角diagonal暂时先返回2D的diagonal的结果
        double dx = fabs(node1->coord.x() - node2->coord.x());
        double dy = fabs(node1->coord.y() - node2->coord.y());
        double dz = fabs(node1->coord.z() - node2->coord.z());
        double tmp_min = std::min(min(dx, dy), dz);
        heuristic_value = (dx + dy + dz) + (sqrt3_ - 3) * tmp_min;//助教给的答案公式
    }

    switch( tie_breaker_ ){
        case RULE_1:
            if(heu_== L1)
                tb_rule1_p_ = 1.0 / (Eigen::Vector3d(GLX_SIZE, GLY_SIZE, GLZ_SIZE)).lpNorm<1>();// 1.0/可能path的最大cost
            else if(heu_== L2) {
                tb_rule1_p_ = 1.0 / (Eigen::Vector3d(GLX_SIZE, GLY_SIZE, GLZ_SIZE)).lpNorm<2>();
            } else if(heu_== DIAGONAL) {
                tb_rule1_p_ = 1.0 / (GLX_SIZE + GLY_SIZE + GLZ_SIZE) + (sqrt3_ - 3) * std::min(min(GLX_SIZE, GLY_SIZE), GLZ_SIZE);
            }
            heuristic_value = heuristic_value * (1 + tb_rule1_p_);
//            ROS_DEBUG_STREAM("tie breaker RULE_0 p: " << tb_rule1_p_);//L2 tb_rule1_p_=0.0133333
            break;
        case RULE_2://未来可能的实现
            break;
        case RULE_3:
            break;
        case RULE_4:
            break;
        case RULE_NONE: default:
            break;
    }
    return heuristic_value;
}

void AstarPathFinder::AstarGraphSearch(Vector3d start_pt, Vector3d end_pt)
{   
    ros::Time time_1 = ros::Time::now();    

    //index of start_point and end_point
    Vector3i start_idx = coord2gridIndex(start_pt);
    Vector3i end_idx   = coord2gridIndex(end_pt);
    goalIdx = end_idx;

    //position of start_point and end_point
    start_pt = gridIndex2coord(start_idx);
    end_pt   = gridIndex2coord(end_idx);

    //Initialize the pointers of struct GridNode which represent start node and goal node
    GridNodePtr startPtr = new GridNode(start_idx, start_pt);
    GridNodePtr endPtr   = new GridNode(end_idx,   end_pt);

    //openSet is the open_list implemented through multimap in STL library
    openSet.clear();
    // currentPtr represents the node with lowest f(n) in the open_list
    GridNodePtr currentPtr  = NULL;
    GridNodePtr neighborPtr = NULL;

    //put start node in open set
    startPtr -> gScore = 0;
    startPtr -> fScore = startPtr -> gScore + getHeu(startPtr,endPtr);
    //STEP 1: finish the AstarPathFinder::getHeu , which is the heuristic function
    startPtr -> id = 1; 
    startPtr -> coord = start_pt;
    openSet.insert( make_pair(startPtr -> fScore, startPtr) );//默认按照key升序排序
    /*
    *
    STEP 2 :  some else preparatory works which should be done before while loop
    please write your code below
    *
    *
    */
    double tentative_gScore;
    vector<GridNodePtr> neighborPtrSets;
    vector<double> edgeCostSets;
    //计算graph中所有的node到start_pt的heuristic

    //将start node赋予地图(因为是刚才new出来的，不是直接从地图里面取出来的)
    GridNodeMap[start_idx(0)][start_idx(1)][start_idx(2)] = startPtr;
    // this is the main loop
    while ( !openSet.empty() ){
        /*
        *
        *
        step 3: Remove the node with lowest cost function from open set to closed set
        please write your code below
        
        IMPORTANT NOTE!!!
        This part you should use the C++ STL: multimap, more details can be find in Homework description
        *
        *
        */
        //弹出一个就要找到他所有的未被扩展的邻居
//        ROS_DEBUG("\nhere3");
        currentPtr = openSet.begin()->second;
        openSet.erase(openSet.begin());
        currentPtr->id = -1;//mark as visited

        // if the current node is the goal 
        if( currentPtr->index == goalIdx ){
            ros::Time time_2 = ros::Time::now();
            terminatePtr = currentPtr;
            ROS_WARN("[A*]{sucess}  Time in A*  is %f ms, path cost if %f m", (time_2 - time_1).toSec() * 1000.0, currentPtr->gScore * resolution );            
            return;
        }
        //get the succetion(找到currentPtr的neighbor nodes)
        AstarGetSucc(currentPtr, neighborPtrSets, edgeCostSets);  //STEP 4: finish AstarPathFinder::AstarGetSucc yourself     

        /*
        *
        *
        STEP 5:  For all unexpanded neigbors "m" of node "n", please finish this for loop
        please write your code below
        *        
        */
        //在这个循环里面，id只会为0/1，为-1的都是遍历完之后被erase掉了
        for(int i = 0; i < (int)neighborPtrSets.size(); i++){
            neighborPtr = neighborPtrSets[i];
            tentative_gScore = currentPtr->gScore + edgeCostSets[i];
//            ROS_DEBUG("\nneighborPtr->id: %d", neighborPtr->id);
            /*
            *
            *
            Judge if the neigbors have been expanded
            please write your code below
            
            IMPORTANT NOTE!!!
            neighborPtrSets[i]->id = -1 : expanded, equal to this node is in close set
            neighborPtrSets[i]->id = 1 : unexpanded, equal to this node is in open set
            *        
            */
            if(neighborPtr -> id == 0 ){ //discover a new node, which is not in the closed set and open set
                /*
                *
                *
                STEP 6:  As for a new node, do what you need do ,and then put neighbor in open set and record it
                please write your code below
                *        
                */

                if(neighborPtr -> gScore == inf) {
                    neighborPtr->cameFrom = currentPtr;
                    neighborPtr -> gScore = tentative_gScore;
                    neighborPtr -> fScore = neighborPtr -> gScore + getHeu(neighborPtr, endPtr); //getHeu(startPtr,neighborPtr);
                    neighborPtr -> id = 1;//标记为expanded
                    openSet.insert( make_pair(neighborPtr->fScore, neighborPtr) );//加入到open list中，注意，这里需要使用fscore，而不是gscore，如果是gscore，就成了Dijkstra了
//                    ROS_DEBUG("\nneighborPtr -> gScore is inf");
                    continue;//这里可以直接退出本轮循环，因为下面的条件不会满足
                } else {
                    ROS_DEBUG_STREAM("\nA* here neighborPtr -> gScore is not inf");
                }
            }
            //这里不能取等，去等了如果前面在找neighbors时没有去掉本身，就会陷入自己来自于自己的bug
            if(tentative_gScore < neighborPtr-> gScore){ //this node is in open set and need to judge if it needs to update, the "0" should be deleted when you are coding
                /*
                *
                *
                STEP 7:  As for a node in open set, update it , maintain the openset ,and then put neighbor in open set and record it
                please write your code below
                *        
                */
                neighborPtr -> cameFrom = currentPtr;
                neighborPtr -> gScore = tentative_gScore;
                neighborPtr -> fScore = neighborPtr -> gScore + getHeu(neighborPtr, endPtr);

            }
            //不满足条件的就是在close set中，不用处理，在下次的while循环中会被erase掉
        }      
    }
    //if search fails
    ros::Time time_2 = ros::Time::now();
    if((time_2 - time_1).toSec() > 0.1)
        ROS_WARN("Time consume in Astar path finding is %f", (time_2 - time_1).toSec() );
}


vector<Vector3d> AstarPathFinder::getPath()
{   
    vector<Vector3d> path;
    vector<GridNodePtr> gridPath;
    /*
    *
    *
    STEP 8:  trace back from the curretnt nodePtr to get all nodes along the path
    please write your code below
    *      
    */
    Vector3d end_pt   = gridIndex2coord(goalIdx);
    GridNodePtr tmpPtr = terminatePtr;
//    ROS_DEBUG_STREAM("terminatePtr->gscore: " << tmpPtr->gScore);

    while(tmpPtr->cameFrom != nullptr) { //这两种判断方式都可以，gscore为0或者cameFrome为空
//    while(tmpPtr->gScore != 0) {
        gridPath.emplace_back(tmpPtr);
        tmpPtr = tmpPtr->cameFrom;
    }
    ROS_DEBUG_STREAM("\nhas found start goal, coord: " << tmpPtr->coord.transpose());
    ROS_DEBUG_STREAM("\ninverse path:, gridPath.size()" << gridPath.size() );

    for (auto ptr: gridPath) {
        path.push_back(ptr->coord);
        ROS_DEBUG_STREAM("" << ptr->coord.transpose());
    }
        
    reverse(path.begin(),path.end());

    return path;
}

2. 解

2.1 A* 不同heuristic的对比

一些设置：

1. 在random_complex_generator.cpp固定随机种子固定生成的地图

void RandomMapGenerate()
{  
//   random_device rd;
//   default_random_engine eng(rd());
    default_random_engine eng(40); // 使用42作为种子(unsigned int类型),使得每次生成的地图是固定的
    ...
}

2. 由于每次手动点击设置goal会存在偏差，于是在demo_node.cpp中固定goal

void rcvWaypointsCallback(const nav_msgs::Path & wp)
{     
    if( wp.poses[0].pose.position.z < 0.0 || _has_map == false )
        return;

    Vector3d target_pt;
//    target_pt << wp.poses[0].pose.position.x,
//                 wp.poses[0].pose.position.y,
//                 wp.poses[0].pose.position.z;
    target_pt << 4.90,4.90,0; //设为固定的用于对比
    ROS_INFO("\n[node] receive the planning target, start is: (%f, %f, %f), target is: (%f, %f, %f)",
             _start_pt(0), _start_pt(1), _start_pt(2), target_pt(0), target_pt(1), target_pt(2));
    pathFinding(_start_pt, target_pt); 
}

3. 设置：无tie breaker，heuristic有四个：0，L1，L2，Diagonal
   2D Diagonal heuristic：$$h=(dx+dy)+D\ast (\sqrt{2}-2)\ast min(dx,dy)$$
   3D Diagonal heuristic：$$h=(dx+dy+dz)+D\ast (\sqrt{3}-3)\ast min(dx,dy,dz)$$
   其中
   $D$为沿着一个轴移动的成本（通常设为1），
   $$\begin{gathered} dx=|x_{node1}-x_{node2}| \\ dy=|y_{node1}-y_{node2}| \\ dz=|z_{node1}-z_{node2}| \end{gathered}$$
   运行结果实例截图：
   
   
   结果：
   虽然做了上述设置，但每次运行时间还是不同，所以多做几次取平均值：
4. 0 heuristic

组号	Heuristic	time(ms)	path cost
1	0	12.401852	9.106062
2	0	12.944236	9.106062
3	0	12.540016	9.106062
4	0	12.005185	9.106062
avg	0	12.47282225	9.106062

2. L1 heuristic

组号	Heuristic	time(ms)	path cost
1	L1	11.930942	9.106062
2	0	12.116784	9.106062
3	0	11.759542	9.106062
4	0	11.780423	9.106062
avg	0	11.89692275	9.106062

3. L2 heuristic

组号	Heuristic	time(ms)	path cost
1	L1	12.830061	9.106062
2	0	13.720000	9.106062
3	0	13.756997	9.106062
4	0	13.889060	9.106062
avg	0	13.5490295	9.106062

4. Diagonal heuristic

组号	Heuristic	time(ms)	path cost
1	L1	12.651738	9.106062
2	0	12.741407	9.106062
3	0	14.569988	9.106062
4	0	12.993555	9.106062
avg	0	13.239172	9.106062

5. avg对比
   path cost相同，都是最优，只比较时间：

Heuristic	time(ms)
0	12.47282225
L1	11.89692275
L2	13.5490295
Diagonal	13.239172

在这张地图和goal的设置中，使用L1 heuristic相较0 heuristic来说搜索时间有所缩短，L2和Diagonal都使搜索时间增加，这里仅作参考，具体heuristic的作用针对不同goal和地图可能不同。

2.2 Tie breaker对A* 的影响

同样按照2.1中的设置，heuristic固定为Diagonal，对A* 施加RULE_1的tie breaker：

在计算Heuristic时加入一个系数p，计算$h^{\prime }=h\ast (1+p)$$$p=\frac{一步的最小cost}{可能的path的最大cost(比如矩形地图的斜对角线cost)}$$

该部分代码如下：

double AstarPathFinder::getHeu(GridNodePtr node1, GridNodePtr node2)
{
    if(!node1 || !node2) {
        ROS_ERROR("Invalid node pointer");
        return std::numeric_limits<double>::infinity(); // 或其他错误处理方式
    }
    double heuristic_value;
    if( heu_ == ZERO ) {
        return 0;
    } else if ( heu_ == L1 ) {
        heuristic_value = (node1->coord-node2->coord).lpNorm<1>();
    } else if ( heu_ == L2 ) {
        heuristic_value = (node1->coord-node2->coord).lpNorm<2>();
    } else if ( heu_ == DIAGONAL ) {//对角diagonal暂时先返回2D的diagonal的结果
        double dx = fabs(node1->coord.x() - node2->coord.x());
        double dy = fabs(node1->coord.y() - node2->coord.y());
        double dz = fabs(node1->coord.z() - node2->coord.z());
        double tmp_min = std::min(min(dx, dy), dz);
        heuristic_value = (dx + dy + dz) + (sqrt3_ - 3) * tmp_min;
    }

    switch( tie_breaker_ ){
        case RULE_1:
            if(heu_== L1)
                tb_rule1_p_ = 1.0 / (Eigen::Vector3d(GLX_SIZE, GLY_SIZE, GLZ_SIZE)).lpNorm<1>();// 1.0/可能path的最大cost
            else if(heu_== L2) {
                tb_rule1_p_ = 1.0 / (Eigen::Vector3d(GLX_SIZE, GLY_SIZE, GLZ_SIZE)).lpNorm<2>();
            } else if(heu_== DIAGONAL) {
                tb_rule1_p_ = 1.0 / (GLX_SIZE + GLY_SIZE + GLZ_SIZE) + (sqrt3_ - 3) * std::min(min(GLX_SIZE, GLY_SIZE), GLZ_SIZE);
            }
            heuristic_value = heuristic_value * (1 + tb_rule1_p_);
//            ROS_DEBUG_STREAM("tie breaker RULE_0 p: " << tb_rule1_p_);//L2 tb_rule1_p_=0.0133333
            break;
        case RULE_2://未来可能的实现
            break;
        case RULE_3:
            break;
        case RULE_4:
            break;
        case RULE_NONE: default:
            break;
    }
    return heuristic_value;
}

1. 无tie breaker

组号	tie breaker	time(ms)	path cost
1	NO	13.050096	9.106062
2	NO	12.888861	9.106062
3	NO	13.205173	9.106062
4	NO	13.281006	9.106062
5	NO	12.602840	9.106062
6	NO	13.001383	9.106062
7	NO	12.626246	9.106062
8	NO	13.128497	9.106062
avg	NO	12.97301275	9.106062

2. RULE_1 tie breaker

组号	tie breaker	time(ms)	path cost
1	RULE_1	14.896261	9.106062
2	RULE_1	16.362376	9.106062
3	RULE_1	15.170169	9.106062
4	RULE_1	15.184500	9.106062
5	RULE_1	15.019135	9.106062
6	RULE_1	14.946042	9.106062
7	RULE_1	15.375405	9.106062
8	RULE_1	15.038559	9.106062
avg	RULE_1	15.249055875	9.106062

3. avg对比
   path cost同样都是最优。

tie breaker	time(ms)
NO	12.97301275
RULE_1	15.249055875

从本组实验中可以看出，加入tie breaker使A* 的搜索时间增加，但仍是最优路径，结果仅做参考。

2.3 A*与JPS对比

由于JPS部分比较复杂，课程作业给出了rules，主要是在JPSGetSucc()函数中判断是否jump成功以及使用Look ahead rules和Jumping rules，根据A的实现方法，我实现了JPS，但是在对比过程中经常发现JPS搜索耗时比A长，且path cost经常比A*稍微大一点，所以JPS可能是存在问题，但是由于最核心的rules不是自己实现的，所以debug起来有些困难，所以JPS部分实验没办法开展，贴个图：

来自GPT4.0的结论：

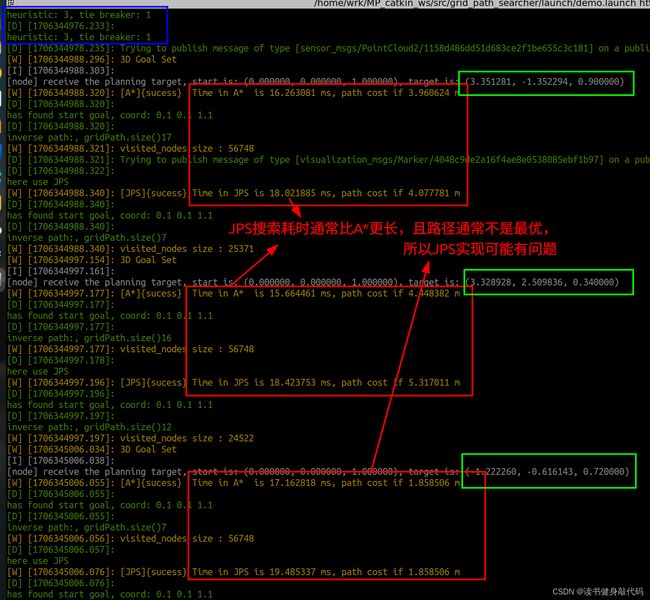
总结：

• 空旷场景JPS可坑更快，障碍物多；地形复杂时A* 可能更好，此时JPS优势可能不明显。
• JPS只能在D相同的grid map中使用，其他map无法使用，但是A*可以使用。

2.4 过程中遇到的问题

2.4.1 地图分辨率

motion planning中对于地图有分辨率(resolution)的概念

    nh.param("map/resolution",    _resolution,   0.2);
    _inv_resolution = 1.0 / _resolution;//分辨率0.2，逆分辨率即5
    
    _max_x_id = (int)(_x_size * _inv_resolution);
    _max_y_id = (int)(_y_size * _inv_resolution);
    _max_z_id = (int)(_z_size * _inv_resolution);

降低分辨率会导致空间开销进一步减小，算法速度加快，但精度会降低，例如，如果将 _resolution 的值从0.2降低到0.1，那么每个栅格代表的实际世界空间的大小就从5格降低到10格。修改分辨率是精度与效率的trade-off。

---

2.4.2 JPS粗略理解

JPSGetSucc函数用于进行jump，并判断是否jump成功。
其中，JPS3DNeib是重要的数据结构，

• ns 总会被add的node
• f1：可能是force neighbor的节点
• f2：这个应该是straight recall的要被扩展的节点
• nsz：4种L1 norm对应的{always added, neighbors to add if forced}

jump函数是递归函数，如果发现存在isOccupied的neighbor，则jump返回true，

num_neib + num_fneib = always added+ neighbors to add if forced是一次扩展最多query的node个数

先query所有always added node，再query所有neighbors to add if forced。
在过程中如果发现了forced neighbor(即jump返回true，即发现了occupied)，则记录扩展的方向(从currentPtr的index三个方向上个增加了多少，这个增加量就是expandDir扩展方向)，并且将这个存在force neighbor的node(index为neighborIdx)加到open list中，并计算edgeCostSets（当前节点indexcurrentPtr->index和存在forced node的indexneighborIdx的欧氏距离），即g。

2.4.3 some bugs

四个错误：

1. openSet.insert( make_pair(neighborPtr->fScore, neighborPtr) )这里我用的是gscore，应该用fscore
2. 算hscore的时候，应该是当前node到end node，而不是start node到当前node
   我的错误代码：

neighborPtr -> fScore = neighborPtr -> gScore + getHeu(startPtr,neighborPtr); //getHeu(startPtr,neighborPtr);

正确代码：

neighborPtr -> fScore = neighborPtr -> gScore + getHeu(neighborPtr, endPtr); //getHeu(startPtr,neighborPtr);

3. 计算gscore进行更新时计算错误，要从curPtr加上edgeCost与之前的neighborPtr中保存的从别的路径到的cost相比，意思是：从curPtr到neighborPtr有不止一条路，现在尝试的这条路与之前保存的进行相比，不要比错了。我用了下面的错误的代码

tentative_gScore = neighborPtr->gScore + edgeCostSets[i];
if(tentative_gScore < neighborPtr-> gScore){ 
	neighborPtr -> cameFrom = currentPtr;
	neighborPtr -> gScore = tentative_gScore;
	neighborPtr -> fScore = neighborPtr -> gScore + getHeu(neighborPtr, endPtr);
}

我这样写，下面那个if永远进不去。
上面第一句应该改为

tentative_gScore = currentPtr->gScore + edgeCostSets[i];

对算法理解不深入。

4. 一个bug，在main中，忘了对JPS设置heuristic。