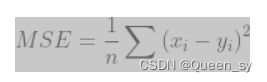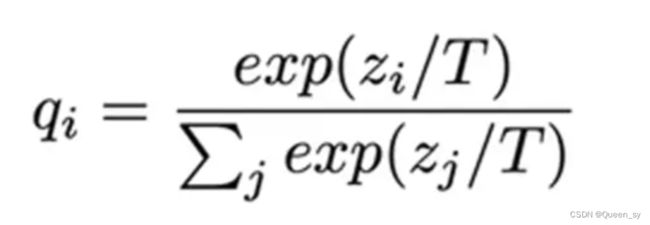【论文解读】Document-Level Relation Extraction with Adaptive Focal Loss and Knowledge Distillation
目录
1 Introduction
1 Docre任务比句子级任务更具挑战性:
2 现有的Docre方法:
3 现有的Docre方法存在三个局限性
2 Methodology
1 使用轴向注意力模块作为特征提取器:
2 第二,提出适应性焦距损失
3 第三用知识蒸馏
相关知识
类别不平衡问题
长尾类分布
交叉熵损失和二元交叉熵损失
二元交叉熵损失定义为
知识蒸馏
全文翻译![]() https://baijiahao.baidu.com/s?id=1737867122728782568&wfr=spider&for=pc
https://baijiahao.baidu.com/s?id=1737867122728782568&wfr=spider&for=pc
Document-Level Relation Extraction with Adaptive Focal Loss and Knowledge Distillation
文档级关系抽取(DocRE) 目的是同时从多个句子中提取关系/文档中多个实体之间的关系
半监督框架,并且有三个新颖点。
第一,使用了一个轴向注意力模块来学习实体对的相关性;
轴向注意模块学习实体对之间的相互依赖关系提高了两跳关系的性能
第二,提出了一个适应性焦距损失来解决DocRE的类不平衡问题;
第三,使用知识蒸馏来克服人类标注数据与远程监督数据的差异性。
1 Introduction
1 Docre任务比句子级任务更具挑战性:
- Docre的复杂度随实体数量的增加呈二次增长。 如果一个文档包含n个实体,则必须对n(n-1)个实体对进行分类决策,并且大多数实体对不包含任何关系。
- 除了正反例不平衡外,正实体对的关系类型分布也高度不平衡。
2 现有的Docre方法:
利用依赖信息来构造DocumentLevel图(Zeng et al.,2021;Zeng et al.,2020),然后使用图神经网络进行推理。 该领域的另一个流行趋势是使用仅transformer(Vaswani et al.,2017)体系结构(Zhou et al.,2021;Xu et al.,2021;Zhang et al.,2021)。 这种模型不需要显式的图推理就能实现状态的性能,表明预训练语言模型能够隐式地捕捉远距离关系。
3 现有的Docre方法存在三个局限性
- 首先,现有的方法主要关注PRLMS的句法特征,而忽略了实体对之间的交互作用。 张等人。 (2021)和李等人 (2021)已经使用CNN结构来编码实体对之间的相互作用,但CNN结构不能捕获两跳推理路径内的所有元素。 (论文中的句法特征就是对句子进行依存句法分析(分析词汇间的依存关系,如并列、从属、递进等),得到一条依存句法路径,再把依存句法路径中的各成分作为向量,拼接起来。)
- 其次,以前没有明确地解决Docre的类不平衡问题的工作。 现有的研究(Zhou et al.,2021;Zhang et al.,2021;Zeng et al.,2020)只关注阈值学习在正反例中的平衡,而没有解决正例中的类不平衡问题。
- 最后,针对Docre任务,很少有人讨论采用远距离监督数据的方法。 徐等人。 (2021)已经表明,远距离监督数据能够提高文档级关系抽取的性能。 然而,它只是使用远距离监督的数据以朴素适应对RE模型进行预训练。
2 Methodology
1 使用轴向注意力模块作为特征提取器:
目的:为了提升对两跳信息的推断。这个模块使我们能够处理两跳逻辑路径内的元素,并捕获关系三元组之间的相互依赖关系。
2 第二,提出适应性焦距损失
来解决类不平衡问题,这个损失函数能够让长尾分布的类别贡献更多的损失,即更关注这些类别。
3 第三用知识蒸馏
来克服人类标注数据与远程监督数据的差异性。具体来说,首先用少批量的标注数据训练一个教师模型,然后用这个模型来在大批量的远程监督数据上做预测。这些生成的预测作为软标签来预训练学生模型。最后,这个预训练的学生模型在人工标注的数据中做微调。
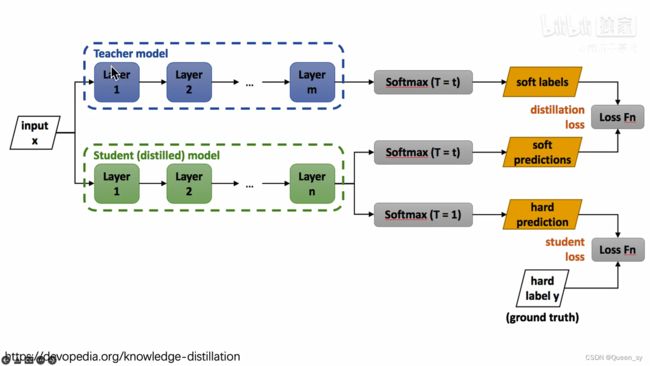
首先有一个已经训练好的教师网络(Teacher model),把很多数据(input)喂给教师网络,教师网络会给每个数据都给一个温度为T的时候的softmax(文中soft labels);同时把数据(input)喂给学生网络(student model),也给学生网络一个温度T获得softmax(文中soft predictions),对soft labels和soft predictions做一个损失函数L(distillation loss也叫soft loss),让他们两个越接近越好,解释就是学生在模拟老师的预测结果;学生网络经过一个T=1的普通的softmax(文中的hard prediction)和hard label再做一个损失函数(student loss也叫hard loss),让他们两个越接近越好。所以这个学生网络既要在温度为T的预测结果和教师网络的预测结果尽可能接近,又要在温度为1的预测结果和标准答案更可能接近。
相关知识
类别不平衡问题
训练数据中某些类别的样本数量极多,而有些类别的样本数量极少,就是所谓的类不平衡(class-imbalance)问题。
比如说一个二分类问题,1000个训练样本,比较理想的情况是正类、负类样本的数量相差不多;而如果正类样本有995个、负类样本仅5个,就意味着存在类不平衡。
在后文中,把样本数量过少的类别称为“少数类”。
但实际上,数据集上的类不平衡到底有没有达到需要特殊处理的程度,还要看不处理时训练出来的模型在验证集上的效果。有些时候是没必要处理的。
长尾类分布
在实际应用中,训练样本通常表现为长尾类分布。位于曲线头部的一小部分类别含有较多数量的样本,剩下的类别含有较少数量的样本。那么,为什么会出现样本数据不平衡的问题呢?例如,在医学图像诊断问题中,需要对CT图像进行识别和分类,较为常见的病症拥有大量的临床实例,因而能够获取大量病症的CT图像,而对于罕见病来说,发病率低,患病人数占比少,相应的CT图像数量就十分匮乏;在自动驾驶问题中,通常情况下的路况都是正常的,很少遇到不正常或者不常见的路况。在这些情况下想要采集大量数据就比较困难。
数据的长尾分布会大大降低模型的泛化性能,出现过拟合的问题。试想一下,如果将分布不均衡的数据不加以任何处理直接输入到模型中进行训练,那么模型必定会在数量较多的样本上学习效果更好,而在数量较小的样本上学习效果更差。
交叉熵损失和二元交叉熵损失
交叉熵损失和二元交叉熵损失
二元交叉熵损失定义为
其中是二元标签值0或者1,是属于标签值的概率。
可以轻易地分析出来,当标签值时,;当标签值时,。也就是说,在二元交叉熵损失函数第一项和第二项之中,必定有一项的值为0。我们再来看第一项和第二项的函数图像(横坐标为,纵坐标为):
当标签值时 ,,如果接近1,接近0;如果接近0, 则变得无穷大。
当标签值时,,如果接近1,变得无穷大;如果接近0,接近0。
通过以上的简单分析,当预测值接近标签值时损失很小,当预测值远离标签值时损失很大,这一特性是有利于模型的学习的。
二元交叉熵(BCE)
这个函数是对数的似然损失的修正。对数列的叠加可以惩罚那些非常自信但是却错误的预测。二元交叉熵损失函数的一般公式为:
— (y . log (p) + (1 — y) . log (1 — p))
让我们继续使用上面例子的值:
输出概率= [0.3、0.7、0.8、0.5、0.6、0.4]
实际的类= [0,1,1,0,1,0]
— (0 . log (0.3) + (1–0) . log (1–0.3)) = 0.155
— (1 . log(0.7) + (1–1) . log (0.3)) = 0.155
— (1 . log(0.8) + (1–1) . log (0.2)) = 0.097
— (0 . log (0.5) + (1–0) . log (1–0.5)) = 0.301
— (1 . log(0.6) + (1–1) . log (0.4)) = 0.222
— (0 . log (0.4) + (1–0) . log (1–0.4)) = 0.222
那么代价函数的结果为:
(0.155 + 0.155 + 0.097 + 0.301 + 0.222 + 0.222) / 6 = 0.192
Python的代码如下:
def BCE (y, y_predicted):
ce_loss = y*(np.log(y_predicted))+(1-y)*(np.log(1-y_predicted))
total_ce = np.sum(ce_loss)
bce = - total_ce/y.size
return bce
损失函数——均方误差(Mean Squared Error,MSE)
均方误差(Mean Squared Error,MSE):MSE是回归任务中常用的损失函数,它衡量模型预测值与实际值之间的平均平方误差。
具体来说,MSE的计算公式如下:
其中,n是样本数量,xi是第i个样本的真实值,yi是模型对第i个样本的预测值。
MSE的值越小,说明模型的预测值与真实值之间的差异越小,模型的性能越好。MSE可以被视为模型对预测值误差的平方的平均值,因此它对离群值(Outlier)比较敏感。如果样本中存在离群值,MSE可能会受到它们的影响而导致模型性能下降。
MSE广泛应用于线性回归和多元线性回归等任务中。在深度学习中,MSE也被用于衡量神经网络在回归任务中的性能,并作为损失函数进行优化。在使用MSE作为损失函数进行优化时,通常会采用梯度下降等优化算法来最小化MSE的值,从而提高模型的性能。
知识蒸馏
知识蒸馏算法原理+综述
举个例子:
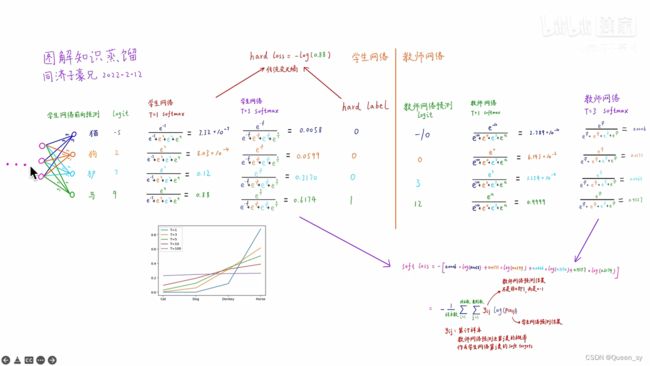
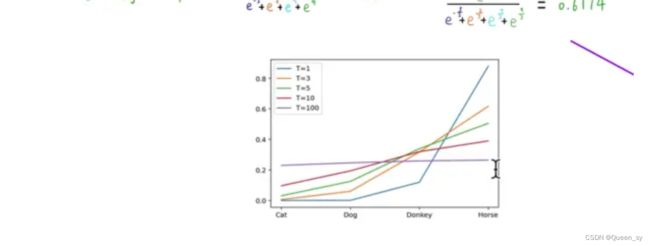
左侧学生网络是个神经网络,四个类别有一个线性分类层,猫的类别给出的分数logit为-5,狗的类别给出的分数logit为2,驴的类别给出的分数logit为7,马的类别给出的分数logit为9
原来的softmax在图中是当T=1时的计算,从计算结果可以看出,有不同数量级,贫富差异较大;
当T=3时,得到的分布就更软了,基本是同一个数量级。但是还是几个数值均分布在0-1之间且和为1
右侧教师网络也是
知识蒸馏的过程
首先有一个已经训练好的教师网络(Teacher model),把很多数据(input)喂给教师网络,教师网络会给每个数据都给一个温度为T的时候的softmax(文中soft labels);同时把数据(input)喂给学生网络(student model),也给学生网络一个温度T获得softmax(文中soft predictions),对soft labels和soft predictions做一个损失函数L(distillation loss也叫soft loss),让他们两个越接近越好,解释就是学生在模拟老师的预测结果;学生网络经过一个T=1的普通的softmax(文中的hard prediction)和hard label再做一个损失函数(student loss也叫hard loss),让他们两个越接近越好。所以这个学生网络既要在温度为T的预测结果和教师网络的预测结果尽可能接近,又要在温度为1的预测结果和标准答案更可能接近。
计算hard loss:学生网络和hard label之间的传统交叉熵为-log(0.88)
计算soft loss:如图
将两个损失函数求和,作为最终学生网络的损失函数,去训练学生网络
知识蒸馏有一个附带的效果:假如用没有3的minist手写数据集去训练学生网络,但是训练教师网络的时候是用的所有类别去训练的,教师网络也会将3的知识迁移给学生网络,虽然学生网络从来没见过3这个类别样本,但是最终学生网络也能预测3。
二、知识蒸馏核心算法
(一)算法
1.问题分析
我们的目标是将大模型的知识迁移到小模型中。那么模型中的“知识”具体是什么呢?
通常认为模型的参数代表知识,但是参数无法迁移,因此需要更加隐式的知识——一种观点是各个类别概率之间的相对大小。相对大小包含了类间关系等更多的隐式信息。
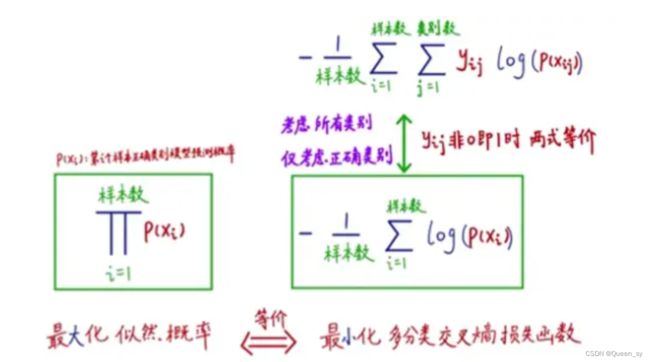
多分类交叉熵损失函数,因为针对每个标签可以给出它属于各个类别的具体概率(而非简单的0-1),因此有助于表示不同类别概率的相对大小。
多分类交叉熵损失函数需要最大化似然概率(所有分类正确)。
数学表示和转化如下:
可知最大化似然概率和最小化多分类交叉熵损失函数是等价的。
为了让学生网络拥有良好的泛化性能,必须学到教师网络中的核心“知识”。
2.思路
参考思路:直接将教师网络预测出的结果作为标签,供学生网络训练。
这种由教师网络生成的标签称为soft targets。相比直接的人工标注,soft targets包含了各个类别的概率,隐含了概率的相对大小、相似性等信息。这种方法学生网络的交叉熵损失函数形式如下:
当类别差别较大时,正确类别和错误类别、错误类别之间概率可能出现相差几个数量级的情况。这时会出现置信度很低(如10^-7或10^-9)的类别,过低的置信度无法表示这些类别之间的相似性。这就需要使置信度的分布更加均匀(所谓soft),不要出现大概率类别和小概率类别集中在两端的情况(所谓hard)。
这种思路的总损失函数由两部分组成:一是soft_loss,表示对教师网络中知识的学习效果;另一种是hard_loss,表示分类效果。
示例如下:
计算学生网络的softmax计算结果和教师网络产生soft target之间的误差即得到soft loss:
3.知识蒸馏算法
(1)T参数
softmax操作:
T是softmax中指数的分母部分,不同T值得到的类别softmax之间的区别如下图:
可见T值越大,越能反映类间的相似性;T值越小,极大概率类别和极小概率类别的差距越明显。
(2)算法结构
上图很清晰地说明了知识蒸馏的算法结构。前面已经知道,总损失=soft_loss+hard_loss。soft_loss的计算方法是增大soft_max中的T以获得充分的类间信息,再计算学生网络softmax和soft target之间的误差(二者T相等)。Hard loss选择较小的T,直接计算分类损失。二者共同构成训练阶段的总损失。
测试阶段只有分类任务、没有学习任务,因此使用hard loss作为损失函数。