【论文精读】RetNet

摘要

       Transformer是大型语言模型的主流架构。然而，transformer的训练并行性是以低效的推理为代价，这使得transformer对部署不友好。不断增长的序列长度会增加GPU内存消耗和延迟，并降低推理速度。许多算法都在继续开发下一代架构，旨在保持训练并行性和transformer的竞争性能，同时具有高效的$O(1)$推理复杂度。但同时实现上述目标是具有挑战性的，即所谓的不可能三角形（如下图）。

       本文提出的算法同时具备低成本的推理、高效的长序列建模、与transformer相当的性能，并同时进行并行模型训练。引入了一种Multi-Scale Retention机制来替代多头注意力，该机制有三种计算范式，即并行、循环和chunkwise循环表示。

• 并行表示使训练并行性能够充分利用GPU设备

• 递归表示能够在内存和计算方面有效地进行O(1)推理。这样可以显著降低部署成本和延迟

• 块递归表示可以进行高效的长序列建模。并行编码每个局部块以提高计算速度，同时反复编码全局块以节省GPU内存

框架

Retention

       给定输入序列$\{x_i{\}}_{i=1}^{|x|}$，经过embedding层得到词嵌入向量$[x_1,\dots ,x_{|x|}]\in {\mathbb{R}}^{|x|\times d}$，$d$为词嵌入维度。对词嵌入向量$X\in {\mathbb{R}}^{|x|\times d}$中的时间步$n$的向量$X_n\in {\mathbb{R}}^{1\times d}$乘以权值$w_v\in {\mathbb{R}}^{d\times d}$得到$v_n\in {\mathbb{R}}^{1\times d}$：

$$v_n=X_n\cdot w_v$$

       乘以可学习权值$W_Q\in {\mathbb{R}}^{d\times d}$、$W_K\in {\mathbb{R}}^{d\times d}$得到query、key向量$Q\in {\mathbb{R}}^{|x|\times d}$、$K\in {\mathbb{R}}^{|x|\times d}$：

$$Q=X{W}_Q，K=X{W}_K$$

       假设上述计算为序列建模问题，通过状态转移迭代计算，状态$s_n\in {\mathbb{R}}^{d\times d}$将$v_n$映射为$o_n$向量，则有：

$$s_n=A{s}_{n-1}+K_n^T{v}_n$$

$$\begin{gathered} o_n=Q_n{s}_n \\ =Q_n(A{s}_{n-1}+K_n^T{v}_n) \\ =Q_n(A(A{s}_{n-2}+K_{n-1}^T{v}_{n-1})+K_n^T{v}_n) \\ =Q_n(A^2{s}_{n-2}+A^1{K}_{n-1}^T{v}_{n-1}+A^0{K}_n^T{v}_n) \\ =Q_n(A^2(A{s}_{n-3}+K_{n-2}^T{v}_{n-2})+A^1{K}_{n-1}^T{v}_{n-1}+A^0{K}_n^T{v}_n) \\ =Q_n(A^3{s}_{n-3}+A^2{K}_{n-2}^T{v}_{n-2}+A^1{K}_{n-1}^T{v}_{n-1}+A^0{K}_n^T{v}_n) \end{gathered}$$

       其中$A\in {\mathbb{R}}^{d\times d}$为位置嵌入矩阵，$Q_n\in {\mathbb{R}}^{1\times d}$、$K_n\in {\mathbb{R}}^{1\times d}$为时间步$n$的query、key投影向量。因为$A^0$为单位阵，假设初始状态$s_0$为全0矩阵，则有：

$$s_1=A{s}_0+K_1^T{v}_1=K_1^T{v}_1$$

       则：

$$\begin{gathered} o_n=Q_n(A^3{s}_{n-3}+A^2{K}_{n-2}^T{v}_{n-2}+A^1{K}_{n-1}^T{v}_{n-1}+A^0{K}_n^T{v}_n) \\ =Q_n(A^{n-(n-3)}{s}_{n-3}+A^{n-(n-2)}{K}_{n-2}^T{v}_{n-2}+A^{n-(n-1)}{K}_{n-1}^T{v}_{n-1}+A^{n-n}{K}_n^T{v}_n) \end{gathered}$$

       归纳得：

$$\begin{gathered} o_n=Q_n(A^{n-1}{K}_1^T{v}_1+A^{n-2}{K}_2^T{v}_2+\cdots +A^{n-(n-2)}{K}_{n-2}^T{v}_{n-2}+A^{n-(n-1)}{K}_{n-1}^T{v}_{n-1}+A^{n-n}{K}_n^T{v}_n) \\ =\sum _{m=1}^n{Q}_n{A}^{n-m}{K}_m^T{v}_m \end{gathered}$$

       给定对角化相对位置嵌入矩阵$A=\Lambda (\gamma e^{i\theta }){\Lambda }^{-1}$，其中$\gamma ,\theta \in {\mathbb{R}}^d$，$\Lambda$为可逆矩阵，$e^{i\theta }=cosx+isinx$，因为$\theta =[{\theta }_1,\dots ,{\theta }_d]$，则有：

$$e^{i\theta }=[cos{\theta }_1,sin{\theta }_2,\dots ,cos{\theta }_{d-1},sin{\theta }_d]$$

       $\gamma e^{i\theta }$是对角阵，对角元素的值为对应将$\gamma$和$e^{i\theta }$转成复数向量相乘再将结果转回实数向量的结果。又因为$\Lambda$为可逆矩阵有${\Lambda }^{-1}\Lambda =I$，则有：

$$\begin{gathered} A^{n-m}=(\Lambda (\gamma e^{i\theta }){\Lambda }^{-1}{)}^{n-m} \\ =\Lambda (\gamma e^{i\theta }){\Lambda }^{-1}\Lambda (\gamma e^{i\theta }){\Lambda }^{-1}\dots \Lambda (\gamma e^{i\theta }){\Lambda }^{-1}\Lambda (\gamma e^{i\theta }){\Lambda }^{-1} \\ =\Lambda (\gamma e^{i\theta }{)}^{n-m}{\Lambda }^{-1} \end{gathered}$$

       则有：

$$\begin{gathered} o_n=\sum _{m=1}^n{Q}_n{A}^{n-m}{K}_m^T{v}_m \\ =\sum _{m=1}^n{Q}_n(\Lambda (\gamma e^{i\theta }{)}^{n-m}{\Lambda }^{-1})K_m^T{v}_m \\ =\sum _{m=1}^n{X}_n{W}_Q\Lambda (\gamma e^{i\theta }{)}^{n-m}{\Lambda }^{-1}{W}_K^T{X}_m^T{v}_m \end{gathered}$$

       因为$\Lambda$、$W_Q$、$W_K$都为可学习向量，故融合得：

$$\begin{gathered} o_n=\sum _{m=1}^n{Q}_n(\gamma e^{i\theta }{)}^{n-m}{K}_m^T{v}_m \\ =\sum _{m=1}^n{Q}_n(\gamma e^{i\theta }{)}^n(\gamma e^{i\theta }{)}^{-m}{K}_m^T{v}_m \\ =\sum _{m=1}^n{Q}_n(\gamma e^{i\theta }{)}^n(K_m(\gamma e^{i\theta }{)}^{-m}{)}^T{v}_m \\ =\sum _{m=1}^n{Q}_n({\gamma }^n{e}^{in\theta })(K_m({\gamma }^{-m}{e}^{i(-m)\theta }){)}^T{v}_m \end{gathered}$$

       设$\gamma$为实数常量，则有：

$$o_n=\sum _{m=1}^n{\gamma }^{n-m}(Q_n{e}^{in\theta })(K_m{e}^{i(-m)\theta }{)}^T{v}_m$$

       因为$cos(-\theta )=cos\theta$、$sin(-\theta )=-sin\theta$，则：

$$\begin{gathered} e^{i(-m)\theta }=[cos-m{\theta }_1,sin-m{\theta }_2,\dots ,cos-m{\theta }_{d-1},sin-m{\theta }_d] \\ =[cosm{\theta }_1,-sinm{\theta }_2,\dots ,cosm{\theta }_{d-1},-sinm{\theta }_d] \end{gathered}$$

       复数形式为：

$$e^{i(-m)\theta }=[cosm{\theta }_1-sinm{\theta }_2,\dots ,cosm{\theta }_{d-1}-sinm{\theta }_d]$$

       因为：

$$e^{im\theta }=[cosm{\theta }_1+sinm{\theta }_2,\dots ,cosm{\theta }_{d-1}+sinm{\theta }_d]$$

       即$e^{i(-m)\theta }$为$e^{im\theta }$的共轭。故得：

$$o_n=\sum _{m=1}^n{\gamma }^{n-m}(Q_n{e}^{in\theta })(K_m{e}^{im\theta }{)}^{†}{v}_m$$

Retention的并行训练表示

       单个时间步$n$得输出为：

$$o_n=\sum _{m=1}^n{\gamma }^{n-m}(Q_n{e}^{in\theta })(K_m{e}^{im\theta }{)}^{†}{v}_m$$

       转换为矩阵的并行表示为：

$$Q=(X{W}_Q)\odot \Theta ，K=(X{W}_K)\odot \bar{\Theta }，V=X{W}_V$$

$${\Theta }_n=e^{in\theta }，D_{nm}=\{\begin{array}{l}{\gamma }^{n-m},n\ge m\\ 0,n<m\end{array}$$

$$Retention(X)=(Q{K}^T\odot D)V$$

       其中$V，Q，K，\Theta \in {\mathbb{R}}^{|x|\times d}$，$D\in {\mathbb{R}}^{|x|\times |x|}$为下三角阵，$\odot$为点乘。该并行表示能够有效地使用gpu训练模型。

       $\Theta ，\tilde{\Theta }$为相对位置嵌入，其通过向量旋转将相对位置信息编码到$Q$和$K$矩阵的每个向量中。

       $D$为因果遮蔽，可作为过去位置的指数衰减加权方案。对于$n<m$的位置，$Q{K}^T$的向量被乘以0，以确保序列处理的因果假设得以实现，不会泄露未来时间步的信息。对于$n\ge m$的位置，$Q{K}^T$的向量被一个指数衰减因子$\gamma$加权，意味着一个标记在过去越远，对于当前的时间步的结果就越不重要，实现了以不同方式权衡前一时间步信息的任务。

Retention的推理循环表示

       因为：

$$\begin{gathered} o_n=\sum _{m=1}^n{\gamma }^{n-m}(Q_n{e}^{in\theta })(K_m{e}^{im\theta }{)}^{†}{v}_m \\ =Q_n{e}^{in\theta }(\sum _{m=1}^n{\gamma }^{n-m}(K_m{e}^{im\theta }{)}^{†}{v}_m) \\ =Q_n{e}^{in\theta }({\gamma }^{n-n}(K_n{e}^{in\theta }{)}^{†}{v}_n+\sum _{m=1}^{n-1}{\gamma }^{n-m}(K_m{e}^{im\theta }{)}^{†}{v}_m) \\ =Q_n{e}^{in\theta }((K_n{e}^{in\theta }{)}^{†}{v}_n+{\gamma }^{n-(n-1)}(K_{n-1}{e}^{i(n-1)\theta }{)}^{†}{v}_{n-1}+\sum _{m=1}^{n-2}{\gamma }^{n-m}(K_m{e}^{im\theta }{)}^{†}{v}_m) \\ =Q_n{e}^{in\theta }((K_n{e}^{in\theta }{)}^{†}{v}_n+\gamma ((K_{n-1}{e}^{i(n-1)\theta }{)}^{†}{v}_{n-1}+\sum _{m=1}^{n-2}{\gamma }^{n-m-1}(K_m{e}^{im\theta }{)}^{†}{v}_m)) \end{gathered}$$

       令：

$$Q_n=Q_n{e}^{in\theta }$$

$$S_{n-1}=(K_{n-1}{e}^{i(n-1)\theta }{)}^{†}{v}_{n-1}+\sum _{m=1}^{n-2}{\gamma }^{n-m-1}(K_m{e}^{im\theta }{)}^{†}{v}_m$$

$$K_n^T{V}_n=(K_n{e}^{in\theta }{)}^{†}{v}_n$$

       则有循环表示：

$$S_n=\gamma S_{n-1}+K_n^T{V}_n$$

$$Retention(X_n)=Q_n{S}_n,n=1,\dots ,|x|$$

       即为下图过程，先计算$K_n$和 $V_n$相乘然后一直累加到状态矩阵$S_n$ 上，最后再和$Q_n$ 相乘，这有利于推理。

Chunkwise递归表示

       并行表征和循环表征的混合形式可以加速训练，将输入序列划分为若干小块。块内按照并行表示进行计算。跨块信息则按照循环表示进行传递。令$B$表示块长度，通过以下方式计算第$i$个分块$x_{[i]}=[x_{(i-1)B+1},\dots ,x_{iB}]$的retention输出：

$$Q_{[i]}=Q_{Bi:B(i+1)}，K_{[i]}=K_{Bi:B(i+1)}，V_{[i]}=V_{Bi:B(i+1)}$$

$$R_i=K_{[i]}^T(V_{[i]}\odot \zeta )+{\gamma }^B{R}_{i-1}，{\zeta }_{ij}={\gamma }^{B-i-1}$$

$$Retention(X_{[i]})=\underset{Inner-Chunk}{(Q_{[i]}{K}_{[i]}^T\odot D)V_{[i]}}+\underset{Cross-Chunk}{(Q_{[i]}{R}_{i-1})\odot \xi }，{\xi }_{ij}={\gamma }^{i+1}$$

Gated Multi-Scale Retention

       Multi-Scale Retention（MSR）每层中可以使用$h=d_{model}/d$个Retention head，其中$d$是head的维度，每个head使用不同的参数矩阵$W_Q,W_K,W_V\in {\mathbb{R}}^{d\times d}$。为每个head分配不同的$\gamma$，不同层之间$\gamma$相同。此外，添加swish gate来增加保留层的非线性。给定输入$X$，将单一层定义为:

$$\gamma =1-2^{-5-arange(0,h)}\in {\mathbb{R}}^h$$

$$hea{d}_i=Retention(X,{\gamma }_i)$$

$$Y=GroupNor{m}_h(Concat(hea{d}_1,\dots ,hea{d}_h))$$

$$MSR(X)=(swish(X{W}_G)\odot Y)W_O$$

       $W_G,W_O\in {\mathbb{R}}^{d_{model}\times d_{model}}$为可学习参数，head使用多个$\gamma$尺度，这将导致不同的方差，故用GroupNorm对每个头的输出分别标准化。整体流程如如下伪代码。

Retention Score 标准化

       可以利用GroupNorm的尺度不变性来提高rentention层的数值精度。因为$GroupNorm(\alpha \ast hea{d}_i)=GroupNorm(hea{d}_i)$，在GroupNorm内乘以标量值不会影响输出和反向梯度。故对并行表示中的三个归一化因子，将$Q{K}^T$标准化为 $Q{K}^T/\sqrt{d}$ ，将$D$替换为${\tilde{D}}_{nm}=D_{nm}/\sqrt{{\sum }_{i=1}^n{D}_{ni}}$ 。令$R=Q{K}^T\odot D$表示Retention Score，将其标准化为${\tilde{R}}_{nm}=R_{nm}/max(|{\sum }_{i=1}^n{R}_{ni}|,1)$，则rentention输出变为$Retention(X)=\tilde{R}V$。由于尺度不变性，上述技巧不会影响最终结果，同时能稳定前向和后向传递的数值流。

Retention 网络总体结构

       对于$L$层retnet，将MSR和FFN堆叠起来构建模型。形式上，输入序列$\{x_i{\}}_{i=1}^{|x|}$通过词嵌入层转换为向量。使用打包的嵌入$X^0=[x_1,\dots ,x_{|x|}]\in {\mathbb{R}}^{|x|\times d}$作为输入并计算模型输出$X^L$:

$$Y^l=MSR(LN(X^l))+X^l$$

$$X^{l+1}=FFN(LN(Y^l))+Y^l$$

       其中$LN(\cdot )$使LayerNorm，$FFN(X)=gelu(X{W}_1)W_2$，$W_1,W_2$为参数矩阵。

训练

       采用并行表示和Chunkwise递归表示训练。序列或块内的并行化可有效地利用gpu来加速计算。chunkwise递归对于长序列训练特别有用，在计算量和内存消耗方面都很高效。

推理

       在推理过程中使用递归表示，可拟合自回归解码，$O(1)$复杂性度降低了内存和推理延迟。

实验

参数分配

       论文重新分配MSR和FFN中的参数以进行公平的比较。在Transformers中，自注意力机制大约有$4d^2$个参数，其中$W_Q,W_K,W_V,W_O\in {\mathbb{R}}^{d\times d}$。FFN中有$8d^2$个参数，中间维度为$4d$。RetNet中的rentention有 $8d^2$个参数，其中$W_Q,W_K\in {\mathbb{R}}^{d\times d}$，$W_G,W_V\in {\mathbb{R}}^{d\times 2d}$，$W_O\in {\mathbb{R}}^{2d\times d}$。$V$的头部维度是$Q,K$的两倍。加宽的维度通过$W_O$投影回$d$。为了保持参数数量与Transformer相同，RetNet中FFN的中间维度为$2d$。同时，论文在实验中将头维度设置为256，即queries和keys为256，values为512。在不同模型大小之间保持$\gamma$ 相同，其中$\gamma =1-e^{linspace(log1/32,log1/512,h)}\in {\mathbb{R}}^h$。

       上图显示了不同尺度模型的训练配置，从零开始训练各种大小的语言模型(即1.3B, 2.7B和6.7B)。 训练语料库是从ThePile，C4和TheStack的精选的数据集，开头附加标记来表示序列的开始。训练batch size为4M token，最大长度为2048，用100B个token训练模型，即25k步。使用AdamW优化器$\beta 1=0.9$，$\beta 2=0.98$，权重衰减设置为0.05。 预热步骤为375步，学习率呈线性衰减。参数按照DeepNet进行初始化，以保证训练的稳定性。

       上图为更详细的训练配置。

对比试验

       上图显示了transformer和retnet的各项性能对比，对于7B参数的模型和8k的输入序列长度，可以看到相比于transformer，retnet实现了8.4倍的吞吐量，节省了3.4倍的显存占用，降低了15.6倍的推理延迟。右图可见随着模型参数的增大，retnet具有更小的预测困惑度。

       上图为RetNet与过往骨干网络的对比，可以看到算法同时实现了以往算法无法同时实现的训练并行化、推理低代价、长序列线性存储复杂度。

       上图实验对比了基于Transformer和RetNet的语言模型验证集的困惑度。给出了三种模型尺寸的缩放曲线，即1.3B、2.7B和6.7B，RetNet与transformer取得了相当的结果。除性能外，RetNet训练在实验中相当稳定。实验结果表明，在大型语言模型方面，RetNet是Transformer的有力竞争对手。从经验上看，当模型大小大于2B时，RetNet的性能开始超过Transformer。

       上图进一步比较了不同上下文长度的语言建模结果。使用2048个文本块作为评估数据，并仅计算最后128个单词的困惑度。实验结果表明，RetNet在不同上下文长度下的性能优于Transformer。此外，RetNet可以利用更长的上下文来获得更好的结果。

       上图为retnet在下游任务用6.7B模型评估了零样本和少样本学习。数据集包括HellaSwag（HS）、BoolQ、COPA、PIQA、Winograd、Winogrande和StoryCloze （SC）。准确率数字与图5所示的语言建模困惑度一致。RetNet在零样本和上下文学习上与Transformer取得了相当的性能。

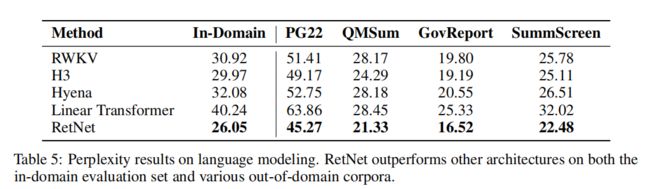
       上图为将RetNet与各种高效的Transformer变体进行了比较，实验在域内验证集和其他域外语料库上计算困惑度，包括Project Gutenberg 2019-2022（PG22），QMSum, GovReport，SummScreen数据集。总的来说，RetNet在不同数据集上的表现优于之前的方法。RetNet不仅在领域内语料上取得了较好的评测结果，而且在多个域外数据集上也获得了较低的困惑度。

此外，比较方法的训练和推理效率，设d表示隐藏维度，n表示序列长度。

• 在训练方面，RWKV的token混合复杂度是$O(dn)$，而Hyena的复杂度是$O(dnlogn)$。上述两种方法通过使用元素操作符来权衡建模容量来减少训练FLOPS。与 Retnet相比，分块循环表示复杂度是$O(dn(b+h))$，通常设置块大小b = 512, 头尺寸h = 256。对于较大的模型大小(即较大的d)或序列长度，额外的b + h的影响可以忽略不计。因此，RetNet训练在不牺牲建模性能的情况下非常高效。

• 推理方面，在比较的高效架构中，Hyena具有与Transformer相同的复杂度$O(n)$，而其他架构为$O(1)$。

训练成本

       上图比较了Transformer和RetNet的训练速度和内存消耗，训练序列长度为8192。还将其与FlashAttention进行了比较，该方法通过重新计算和核融合提高了速度并减少了GPU内存IO。使用chunkwise递归表示留存率，块大小设置为512。

       实验结果表明，RetNet在训练过程中比transformer具有更高的内存效率和吞吐量。即使与FlashAttention相比，RetNet在速度和内存成本上仍然具有竞争力。此外，在不依赖特定内核的情况下，很容易在其他平台上高效地训练RetNet。RetNet具有通过高级实现(如内核融合)进一步降低成本的潜力。

推理成本

       上图在推理期间比较Transformer和RetNet的内存成本、吞吐量和延迟。transformer用解码过的KV标记缓存，RetNet使用循环表 示推理。观察到RetNet在推理成本方面优于Transformer。

       内存成本：由于KV缓存，Transformer的内存成本呈线性增长。相比之下 ，RetNet的内存消耗即使对于长序列也保持一致，只需更少的GPU内存t。RetNet的额外内存消耗几乎可以忽略不计(即大约3％)，而模型权重占97％。

       吞吐量：随着译码长度的增加，Transformer的吞吐量下降。相比之下，RetNet通过利用保留的循环表示，在解码过程中具有更高的长度不变的吞吐量。

       延迟：随着输入的增加，transformer的延迟增长得很快。相比之下，RetNet的解码延迟优于transformer，并在不同的批大小和输入长度上保持几乎相同。

消融实验

       swish gate和GroupNorm：行2、3显示swish gate和GroupNorm两个组件提高RetNet的最终性能。实验表明swish gate模块是增强非线性和改善模型性能的关键。GroupNorm平衡了多头输出的方差，提高了训练稳定性和语言建模结果。

       多尺度衰减：Gated Multi-Scale Retention使用不同的$\gamma$作为保留头的衰减率。行4显示衰减机制和使用多个衰减率都可以提高语言建模的性能。

       head尺寸：head维度暗示了隐藏状态的记忆容量。在消融研究中，将默认头部维度从256减少到64，即query和key为64，value为128，隐藏层维度不变。行5表明，head尺寸越大，性能越好。

reference

Yutao, S. , Li, D. , Shaohan, H. , Shuming, M. , Yuqing, Xia. , Jilong, X. , Jianyong, W. , & Furu, W. . (2023). Retentive Network: A Successor to Transformer for Large Language Models.