2023年十四届蓝桥杯省赛大学B组真题(Java完整版)
2023年十四届蓝桥杯省赛大学B组真题
试题A:阶乘求和
本题总分:5 分
【问题描述】
令 S = 1! + 2! + 3! + … + 202320232023!,求 S 的末尾 9 位数字。 提示:答案首位不为 0。
【答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一 个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
答案:420940313
【解题思路】
对于数据量大的计算题,可以先尝试把每一步的数据结果展示出来,分析规律,而这题恰巧在某一个位置后,末尾9位数字全为0,在此之前的结果就是答案,过程中记得对每个值都进行取余,否则可能会导致数值出错,得不到正确答案。
【代码】
package zhenti_2023_jiechengqiuhe;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
// 在此输入您的代码...
long sum = 0;// 数据量较大,用long
long num = 1;
for (int i = 1; true; i++) {
// 当阶乘后九位为0时,相加无意义
if (num % 1e9 == 0)
break;
num *= i;
// num结果除余对最终结果无影响,不除余会造成数据错误
num %= 1e9;
sum += num;
sum %= 1e9;
}
System.out.println(sum);
scan.close();
}
}
试题 B: 幸运数字
本题总分:5 分
【问题描述】
哈沙德数是指在某个固定的进位制当中,可以被各位数字之和整除的正整 数。例如 126 是十进制下的一个哈沙德数,因为 (126)10 mod (1+2+6) = 0;126也是八进制下的哈沙德数,因为 (126)10 = (176)8,(126)10 mod (1 + 7 + 6) = 0; 同时 126 也是 16 进制下的哈沙德数,因为 (126)10 = (7e)16,(126)10 mod (7 + e) = 0。小蓝认为,如果一个整数在二进制、八进制、十进制、十六进制下均为 哈沙德数,那么这个数字就是幸运数字,第 1 至第 10 个幸运数字的十进制表示 为:1 , 2 , 4 , 6 , 8 , 40 , 48 , 72 , 120 , 126 . . . 。现在他想知道第 2023 个幸运数 字是多少?你只需要告诉小蓝这个整数的十进制表示即可。
【答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一 个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
答案:215040
【解题思路】
给出一个判断是否为哈沙德数的判断式,从1开始一直循环遍历下去,并为符合条件的数标记个数,直到2023个被标记数时,获取当前值,即为答案。
【代码】
package zhenti_2023_xingyunshuzi;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
// 在此输入您的代码...
Main m1 = new Main();
int count = 0;
for (int i = 1; true; i++) {
// 判断是否为幸运数字,是则标记count
if (m1.sfhasha(i, 2) && m1.sfhasha(i, 8) && m1.sfhasha(i, 10) && m1.sfhasha(i, 16))
count++;
else {
continue;
}
// 当count为2023时,输出结果
if (count == 2023) {
System.out.println(i);
break;
}
}
scan.close();
}
/**
*
* @param i 判断是否为哈沙德数的数
* @param mod 判断的进制
* @return 判断i在mod进制下是否为哈沙德数
*/
public boolean sfhasha(int i, int mod) {
int num = i, sum = 0;
boolean sf;
while (i != 0) {
sum += i % mod;// sum为i在mod进制时的值各个位上的数之和
i /= mod;
}
sf = (num % sum) == 0;
return sf;
}
}
试题 C: 数组分割
时间限制: 2.0s 内存限制: 512.0MB 本题总分:10 分
【问题描述】
小蓝有一个长度为 N 的数组 A = [A0, A1, . . . , AN−1]。现在小蓝想要从 A 对应的数组下标所构成的集合 I = 0, 1, 2, . . . , N − 1 中找出一个子集 R1,那么 R1 在 I 中的补集为 R2。记 S 1 = ∑r∈R1 Ar,S 2 = ∑r∈R2 Ar,我们要求 S 1 和 S 2 均为 偶数,请问在这种情况下共有多少种不同的 R1。当 R1 或 R2 为空集时我们将S 1 或 S 2 视为 0。
【输入格式】
第一行一个整数 T,表示有 T 组数据。 接下来输入 T 组数据,每组数据包含两行:第一行一个整数 N,表示数组A 的长度;第二行输入 N 个整数从左至右依次为 A0, A1, . . . , AN−1,相邻元素之 间用空格分隔。
【输出格式】
对于每组数据,输出一行,包含一个整数表示答案,答案可能会很大,你 需要将答案对 1000000007 进行取模后输出。
【样例输入】
2
2
6 6
2
1 6
【样例输出】
4
0
【样例说明】
对于第一组数据,答案为 4。(注意:大括号内的数字表示元素在数组中的 下标。)
R1 = {0}, R2 = {1};此时 S 1 = A0 = 6 为偶数, S 2 = A1 = 6 为偶数。
R1 = {1}, R2 = {0};此时 S 1 = A1 = 6 为偶数, S 2 = A0 = 6 为偶数。
R1 = {0, 1}, R2 = {};此时 S 1 = A0 + A1 = 12 为偶数, S 2 = 0 为偶数。
R1 = {}, R2 = {0, 1};此时 S 1 = 0 为偶数, S 2 = A0 + A1 = 12 为偶数。 对于第二组数据,无论怎么选择,都不满足条件,所以答案为 0。
【评测用例规模与约定】
对于 20% 的评测用例,1 ≤ N ≤ 10。
对于 40% 的评测用例,1 ≤ N ≤ 1 0 2 10^2 102。
对于 100% 的评测用例,1 ≤ T ≤ 10, 1 ≤ N ≤ 1 0 3 10^3 103 , 0 ≤ A i A_i Ai ≤ 1 0 9 10^9 109。
【解题思路】
通过分析,R1需要取一部分的数值,R2则取余下的部分,要想两边和都为偶数需要满足无奇数或奇数个数为偶数个,即题中奇数总个数要为偶数个,否则返回结果0,由于偶数组和奇数组相互独立,根据乘法法则,最终结果为偶数组合数乘以奇数组合数,偶数组合数=pow(2,偶数个数),奇数组合数=pow(2,奇数个数)。
【代码】
package zhenti_2023_shuzufenge;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
// 在此输入您的代码...
int T;// 接收有几组数据
T = scan.nextInt();
int N;// 接收数组A的长度
int[][] A = new int[T][];// 用于存放数组内容
int[] count = new int[T];// 用于存放各组符合条件的个数,即结果答案
// 获取用户输入内容,为数组赋值,并计算结果
for (int i = 0; i < T; i++) {
int i0 = 0, i1 = 0;// i0为偶数个数,i1为奇数个数
N = scan.nextInt();
A[i] = new int[N];
//获取数组中一共有几个奇数和偶数
for (int j = 0; j < N; j++) {
A[i][j] = scan.nextInt();
if (A[i][j] % 2 != 0) {
i1++;
} else {
i0++;
}
}
//一、经对结果进行分析,发现只有当数组奇数个数为偶数个时,才符合结果所需要求
//二、经对结果进行分析,发现结果规律为下列表达式:结果=pow(2,偶数个数)*pow(2,奇数个数-1) 如果奇数个数为0,则pow(2,0)
if(i1%2!=0) {
count[i]=0;
continue;
}else {
count[i]=(int)(Math.pow(2,i0)*Math.pow(2, i1==0?0:i1-1)%1000000007);
}
}
for (int i : count) {
System.out.println(i);
}
}
}
试题 D: 矩形总面积
时间限制: 2.0s 内存限制: 512.0MB 本题总分:10 分
【问题描述】
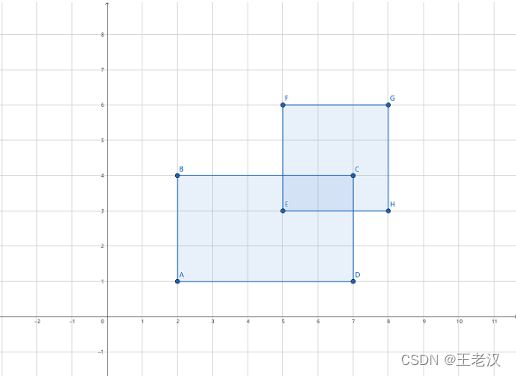
平面上有个两个矩形 R1 和 R2,它们各边都与坐标轴平行。设 (x1, y1) 和(x2, y2) 依次是 R1 的左下角和右上角坐标,(x3, y3) 和 (x4, y4) 依次是 R2 的左下 角和右上角坐标,请你计算 R1 和 R2 的总面积是多少?
注意:如果 R1 和 R2 有重叠区域,重叠区域的面积只计算一次。
【输入格式】
输入只有一行,包含 8 个整数,依次是:x1,y1,x2,y2,x3,y3,x4 和 y4。
【输出格式】
一个整数,代表答案。
【样例输入】
2 1 7 4 5 3 8 6
【样例输出】
22
【样例说明】
【评测用例规模与约定】
对于 20% 的数据,R1 和 R2 没有重叠区域。
对于 20% 的数据,其中一个矩形完全在另一个矩形内部。
对于 50% 的数据,所有坐标的取值范围是 [0, 1 0 3 10^3 103]。
对于 100% 的数据,所有坐标的取值范围是 [0, 1 0 5 10^5 105]。
【解题思路】
求两个矩形合并后的面积,很容易想到先对两个矩形的面积进行求和,再减去重叠部分的面积,如果没重叠,重叠部分面积则为0,如何判断是否重叠,当最小的右上角点坐标的x,y值减去最大左下角点坐标的x,y结果>0即重叠,反之未重叠。
【代码】
package zhenti_2023_juxingzongmianji;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
// 在此输入您的代码...
int x1 = scan.nextInt(), y1 = scan.nextInt();
int x2 = scan.nextInt(), y2 = scan.nextInt();
int x3 = scan.nextInt(), y3 = scan.nextInt();
int x4 = scan.nextInt(), y4 = scan.nextInt();
// 计算面积并且减去重叠部分的面积
long area = (long) (x2 - x1) * (y2 - y1) + (long) (x4 - x3) * (y4 - y3);
int overlapWidth = Math.max(0, Math.min(x2, x4) - Math.max(x1, x3)); // 重叠部分宽度
int overlapHeight = Math.max(0, Math.min(y2, y4) - Math.max(y1, y3)); // 重叠部分高度
if (overlapWidth > 0 && overlapHeight > 0) { // 存在重叠部分
area -= (long) overlapWidth * overlapHeight;
}
System.out.println(area);
}
}
试题 E: 蜗牛
时间限制: 2.0s 内存限制: 512.0MB 本题总分:15 分
【问题描述】
这天,一只蜗牛来到了二维坐标系的原点。 在 x 轴上长有 n 根竹竿。它们平行于 y 轴,底部纵坐标为 0,横坐标分别 为 x1, x2, …, xn。竹竿的高度均为无限高,宽度可忽略。蜗牛想要从原点走到第n 个竹竿的底部也就是坐标 (xn, 0)。它只能在 x 轴上或者竹竿上爬行,在 x 轴 上爬行速度为 1 单位每秒;由于受到引力影响,蜗牛在竹竿上向上和向下爬行 的速度分别为 0.7 单位每秒和 1.3 单位每秒。 为了快速到达目的地,它施展了魔法,在第 i 和 i + 1 根竹竿之间建立了传 送门(0 < i < n),如果蜗牛位于第 i 根竹竿的高度为 ai 的位置 (xi , ai),就可以 瞬间到达第 i + 1 根竹竿的高度为 bi+1 的位置 (xi+1, bi+1),请计算蜗牛最少需要 多少秒才能到达目的地。
【输入格式】
输入共 1 + n 行,第一行为一个正整数 n; 第二行为 n 个正整数 x1, x2, . . . , xn; 后面 n − 1 行,每行两个正整数 ai , bi+1。
【输出格式】
输出共一行,一个浮点数表示答案(四舍五入保留两位小数)。
【样例输入】
3
1 10 11
1 1
2 1
【样例输出】
4.20
【样例说明】
蜗牛路线:
(0, 0) → (1, 0) → (1, 1) → (10, 1) → (10, 0) → (11, 0),花费时间为 1 + 1 /0.7 + 0 + 1 /1.3 + 1 ≈ 4.20
【评测用例规模与约定】
对于 20% 的数据,保证 n ≤ 15;
对于 100% 的数据,保证 n ≤ 1 0 5 10^5 105 ,ai , bi ≤ 1 0 4 10^4 104,xi ≤ 1 0 9 10^9 109。
【解题思路】
这题主要是运用dp算法的思维来解,分析得到两种情况,一种是走到竹竿底部,一种是走到竹竿传送门起点:
dp[0][i]表示从起点走到第i根竹竿底部的时间,
dp[1][i]表示从起点走到第i根竹竿传送门起点的时间。
到达竹竿底部的关系式为
dp[0][i] = Math.min(dp[0][i - 1] + s[i], dp[1][i - 1] + y_end[i] / 1.3);
到达传送门起点要分两种情况讨论,一种是传送门终点在起点上方,另一种则是在下方,关系式为
if (y_end[i] > y_start[i]) {
dp[1][i] = Math.min(dp[0][i] + y_start[i] / 0.7, dp[1][i - 1] + (y_end[i] - y_start[i]) / 1.3);
} else {
dp[1][i] = Math.min(dp[0][i] + y_start[i] / 0.7, dp[1][i - 1] + (y_start[i] - y_end[i]) / 0.7);
}
(s[]存放竹竿间的距离,s[3]为第2根竹竿到第3根竹竿的距离,y_start[i]、y_end[i]分别为第i根竹竿传送门起点、终点在y轴的坐标)
【代码】
package zhenti_2023_woniu;
import java.text.DecimalFormat;
import java.util.Scanner;
//1:无需package
//2: 类名必须Main, 不可修改
public class Main {
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
// 在此输入您的代码...
int n = scan.nextInt();// 存放竹竿总数
int[] x = new int[n + 1];// 存放竹竿在x轴的位置
int[] s = new int[n + 1];// 存放竹竿间的距离,s[3]为第2根竹竿到第3根竹竿的距离
int[] y_start = new int[n + 1];// 存放竹竿传送门起点在y轴的位置
int[] y_end = new int[n + 1];// 存放竹竿传送门终点在y轴的位置
// dp[0][i]表示从起点走到第i根竹竿底部的时间,dp[1][i]表示从起点走到第i根竹竿传送门起点的时间
double[][] dp = new double[2][n + 1];
for (int i = 1; i <= n; i++) {
x[i] = scan.nextInt();
s[i] = x[i] - x[i - 1];
}
for (int i = 1; i < n; i++) {
y_start[i] = scan.nextInt();
y_end[i + 1] = scan.nextInt();
}
// y_end[1]、dp[1][0]均为不存在的值,初始化为integer的最大值
y_end[1] = Integer.MAX_VALUE;
dp[1][0] = Integer.MAX_VALUE;
// dp算法
for (int i = 1; i <= n; i++) {
dp[0][i] = Math.min(dp[0][i - 1] + s[i], dp[1][i - 1] + y_end[i] / 1.3);
// 当终点在起点上方,向下爬,反之向上爬
if (y_end[i] > y_start[i]) {
dp[1][i] = Math.min(dp[0][i] + y_start[i] / 0.7, dp[1][i - 1] + (y_end[i] - y_start[i]) / 1.3);
} else {
dp[1][i] = Math.min(dp[0][i] + y_start[i] / 0.7, dp[1][i - 1] + (y_start[i] - y_end[i]) / 0.7);
}
}
// 保留小数点后两位
// DecimalFormat用于格式化十进制数字。
DecimalFormat df = new DecimalFormat("#.00");
System.out.println(df.format(dp[0][n]));
scan.close();
}
}
试题 F: 合并区域
时间限制: 3.0s 内存限制: 512.0MB 本题总分:15 分
【问题描述】
小蓝在玩一款种地游戏。现在他被分配给了两块大小均为 N × N 的正方形 区域。这两块区域都按照 N × N 的规格进行了均等划分,划分成了若干块面积 相同的小区域,其中每块小区域要么是岩石,要么就是土壤,在垂直或者水平 方向上相邻的土壤可以组成一块土地。现在小蓝想要对这两块区域沿着边缘进 行合并,他想知道合并以后可以得到的最大的一块土地的面积是多少(土地的 面积就是土地中土壤小区域的块数)? 在进行合并时,小区域之间必须对齐。可以在两块方形区域的任何一条边 上进行合并,可以对两块方形区域进行 90 度、180 度、270 度、360 度的旋转, 但不可以进行上下或左右翻转,并且两块方形区域不可以发生重叠。
【输入格式】
第一行一个整数 N 表示区域大小。 接下来 N 行表示第一块区域,每行 N 个值为 0 或 1 的整数,相邻的整数 之间用空格进行分隔。值为 0 表示这块小区域是岩石,值为 1 表示这块小区域 是土壤。 再接下来 N 行表示第二块区域,每行 N 个值为 0 或 1 的整数,相邻的整 数之间用空格进行分隔。值为 0 表示这块小区域是岩石,值为 1 表示这块小区 域是土壤。
【输出格式】
一个整数表示将两块区域合并之后可以产生的最大的土地面积。
【样例输入】
4
0 1 1 0
1 0 1 1
1 0 1 0
1 1 1 0
0 0 1 0
0 1 1 0
1 0 0 0
1 1 1 1
【样例输出】
15
【样例说明】
第一张图展示了样例中的两块区域的布局。第二张图展示了其中一种最佳 的合并方式,此时最大的土地面积为 15。

【评测用例规模与约定】
对于 30% 的数据,1 ≤ N ≤ 5。
对于 60% 的数据,1 ≤ N ≤ 15。
对于 100% 的数据,1 ≤ N ≤ 50。
【解题思路】
对两个土地面积的旋转、位移等所有情况进行比对,取出最大面积。
将两个小区域合并成大区域后,空位处默认为0,对每个符合条件的点进行dfs算法,求出本次土地面积(已经探索过的点无需再进行dfs)。
【代码】
package zhenti_2023_hebingquyu;
import java.util.Scanner;
//1:无需package
//2: 类名必须Main, 不可修改
public class Main {
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
// 在此输入您的代码...
Main m = new Main();
int N = scan.nextInt();// 获取N的大小
int[][] land1 = new int[N][N];// 区域1的初始
int[][] land2 = new int[N][N];// 区域2的初始
// 获取两块土地中小区域的规划
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
land1[i][j] = scan.nextInt();
}
}
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
land2[i][j] = scan.nextInt();
}
}
// 分别存放区域1顺时针旋转90、180、270度后的结果
int[][] land1_90 = m.clockwise_90(land1);
int[][] land1_180 = m.clockwise_90(land1_90);
int[][] land1_270 = m.clockwise_90(land1_180);
// 分别存放区域2顺时针旋转90、180、270度后的结果
int[][] land2_90 = m.clockwise_90(land2);
int[][] land2_180 = m.clockwise_90(land2_90);
int[][] land2_270 = m.clockwise_90(land2_180);
// 合并1、2区域后,多余的位置补上0,合并成一个大矩形
// 定义二维数组行为y坐标,列为x坐标,大矩形左上角为(0,0),视作第一象限在(0,0)右下方向
// 区域1的每个角度都要与区域2的每个角度的不同位置进行组合,获得大矩形,相同的两面一共要进行2N-1次不同位置组合
int count = 2 * N - 1;// 区域1右上角与区域2的左下角的偏移量
int max = 0;// 用于存放最大土地面积
// 创建三维数组存放二维数组
int[][][] lands1 = { land1, land1_90, land1_180, land1_270 };
int[][][] lands2 = { land2, land2_90, land2_180, land2_270 };
// 创建四维数组存放数组数据进行操作
int[][][][] lands = { lands1, lands2 };
// 循环调用求土地面积方法,并通过比对求得最大面积max
while (count > 0) {
for (int i = 0; i < 4; i++) {
for (int j = 0; j < 4; j++) {
if (max < m.max_arer(m.combine(lands[0][i], lands[1][j], count))) {
max = m.max_arer(m.combine(lands[0][i], lands[1][j], count));
}
}
}
count--;
}
System.out.println(max);
scan.close();
}
/**
* 求顺时针旋转九十度后的结果
*
* @param land 需要顺时针旋转九十度的区域
* @return 顺时针旋转九十度后的结果
*/
public int[][] clockwise_90(int[][] land) {
int N = land.length;
int[][] land_90 = new int[N][N];
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
land_90[i][j] = land[N - j - 1][i];
}
}
return land_90;
}
/**
* 求两个小区域组合后的大区域,空位补0,凑成大矩形
*
* @param land1 区域1
* @param land2 区域2
* @param count 区域1右上角与区域2的左下角的偏移量
* @return 组合后的大矩形
*/
public int[][] combine(int[][] land1, int[][] land2, int count) {
int N = land1.length;
int[][] land;
// count>=N时,区域1位于大矩形的左上角
if (count >= N) {
land = new int[count][2 * N];
for (int i = 0; i < count; i++) {
for (int j = 0; j < 2 * N; j++) {
if (i < N && j < N) {
land[i][j] = land1[i][j];
} else if (i >= count - N && j >= N) {
land[i][j] = land2[i - count + N][j - N];
}
}
}
}
// count
else {
land = new int[2 * N - count][2 * N];
for (int i = 0; i < 2 * N - count; i++) {
for (int j = 0; j < 2 * N; j++) {
if (i < N && j >= N) {
land[i][j] = land2[i][j - N];
} else if (i >= N - count && j < N) {
land[i][j] = land1[i - (N - count)][j];
}
}
}
}
return land;
}
/**
* 求该区域的最大土地面积
*
* @param land 需要求的区域
* @return 该区域的最大土地面积
*/
public int max_arer(int[][] land) {
int max = 0;
int[][] land_fj = new int[land.length][land[0].length];
for (int i = 0; i < land.length; i++) {
for (int j = 0; j < land[0].length; j++) {
land_fj[i][j] = land[i][j];
}
}
for (int i = 0; i < land.length; i++) {
for (int j = 0; j < land[0].length; j++) {
if (land_fj[i][j] == 1) {
int num = land_dfs(i, j, land_fj);
if (max < num) {
max = num;
}
}
}
}
return max;
}
/**
* 求一个区域从(x,y)点起始的最大土地面积
*
* @param y 数组行坐标
* @param x 数组列坐标
* @param land 所求区域
* @return 该区域从(x,y)点起始的最大土地面积
*/
public int land_dfs(int y, int x, int[][] land) {
int num = 0;
if (land[y][x] == 0) {
return num;
} else if (land[y][x] == 1) {
land[y][x] = 0;
num++;
}
if (y > 0 && land[y - 1][x] == 1) {
num += land_dfs(y - 1, x, land);
}
if (y < land.length - 1 && land[y + 1][x] == 1) {
num += land_dfs(y + 1, x, land);
}
if (x > 0 && land[y][x - 1] == 1) {
num += land_dfs(y, x - 1, land);
}
if (x < land[0].length - 1 && land[y][x + 1] == 1) {
num += land_dfs(y, x + 1, land);
}
return num;
}
}
试题 G: 买二赠一
时间限制: 2.0s 内存限制: 512.0MB 本题总分:20 分
【问题描述】
某商场有 N 件商品,其中第 i 件的价格是 Ai。现在该商场正在进行 “买二 赠一” 的优惠活动,具体规则是: 每购买 2 件商品,假设其中较便宜的价格是 P(如果两件商品价格一样, 则 P 等于其中一件商品的价格),就可以从剩余商品中任选一件价格不超过 P/2的商品,免费获得这一件商品。可以通过反复购买 2 件商品来获得多件免费商品,但是每件商品只能被购买或免费获得一次。 小明想知道如果要拿下所有商品(包含购买和免费获得),至少要花费多少 钱?
【输入格式】
第一行包含一个整数 N。 第二行包含 N 个整数,代表 A1, A2, A3, . . . ,AN。
【输出格式】
输出一个整数,代表答案。
【样例输入】
7
1 4 2 8 5 7 1
【样例输出】
25
【样例说明】
小明可以先购买价格 4 和 8 的商品,免费获得一件价格为 1 的商品;再后 买价格为 5 和 7 的商品,免费获得价格为 2 的商品;最后单独购买剩下的一件 价格为 1 的商品。总计花费 4 + 8 + 5 + 7 + 1 = 25。不存在花费更低的方案。
【评测用例规模与约定】
对于 30% 的数据,1 ≤ N ≤ 20。
对于 100% 的数据,1 ≤ N ≤ 5 × 1 0 5 10^5 105,1 ≤ Ai ≤ 1 0 9 10^9 109 。
【解题思路】
运用贪心算法计算,最优解为优先赠送现存最贵的商品,无法赠送时优先购买最贵的商品,以获取最大赠送金额
【代码】
package zhenti_2023_maierzengyi;
import java.util.Arrays;
import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;
//1:无需package
//2: 类名必须Main, 不可修改
public class Main {
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
// 在此输入您的代码...
Main m = new Main();
int N = scan.nextInt();
int[] prices = new int[N];// int足以存放商品单价的大小
for (int i = 0; i < N; i++) {
prices[i] = scan.nextInt();
}
System.out.println(m.minimum_cost(prices));
scan.close();
}
/**
* 贪心算法计算,最优解为优先赠送现存最贵的商品,无法赠送时优先购买最贵的商品,以获取最大赠送金额
*
* @param prices 单价数组
* @return 最低花费金额
*/
public long minimum_cost(int[] prices) {
long cost = 0;// 存放总花费金额,数值较大用long
boolean second = false;// 判断是否为第二件购买的商品
Queue<Integer> queue = new LinkedList<Integer>();// 创建队列存放可免费赠送商品的最大价格
Arrays.sort(prices);// 对价格数组进行升序排序
int len = prices.length - 1;// 存放数组最大下标,进行逆序访问
while (len >= 0) {
if (!queue.isEmpty() && prices[len] <= queue.peek()) {
// 当队列不为空且当前商品满足免费赠送条件时,对赠送商品进行出队操作
queue.poll();
} else {
// 当当前商品无法赠送时,进行购买操作
cost += prices[len];
if (second) {
// 当商品是第二件购买的商品,符合赠送条件,入队可赠送价格
queue.add(prices[len] / 2);
second = false;
} else {
second = true;
}
}
len--;
}
return cost;
}
}
试题 H: 合并石子
时间限制: 2.0s 内存限制: 512.0MB 本题总分:20 分
【问题描述】
在桌面从左至右横向摆放着 N 堆石子。每一堆石子都有着相同的颜色,颜 色可能是颜色 0,颜色 1 或者颜色 2 中的其中一种。 现在要对石子进行合并,规定每次只能选择位置相邻并且颜色相同的两堆 石子进行合并。合并后新堆的相对位置保持不变,新堆的石子数目为所选择的 两堆石子数目之和,并且新堆石子的颜色也会发生循环式的变化。具体来说: 两堆颜色 0 的石子合并后的石子堆为颜色 1,两堆颜色 1 的石子合并后的石子 堆为颜色 2,两堆颜色 2 的石子合并后的石子堆为颜色 0。本次合并的花费为所 选择的两堆石子的数目之和。 给出 N 堆石子以及他们的初始颜色,请问最少可以将它们合并为多少堆石 子?如果有多种答案,选择其中合并总花费最小的一种,合并总花费指的是在 所有的合并操作中产生的合并花费的总和。
【输入格式】
第一行一个正整数 N 表示石子堆数。 第二行包含 N 个用空格分隔的正整数,表示从左至右每一堆石子的数目。 第三行包含 N 个值为 0 或 1 或 2 的整数表示每堆石头的颜色。
【输出格式】
一行包含两个整数,用空格分隔。其中第一个整数表示合并后数目最少的 石头堆数,第二个整数表示对应的最小花费。
【样例输入】
5
5 10 1 8 6
1 1 0 2 2
【样例输出】
2 44
【样例说明】
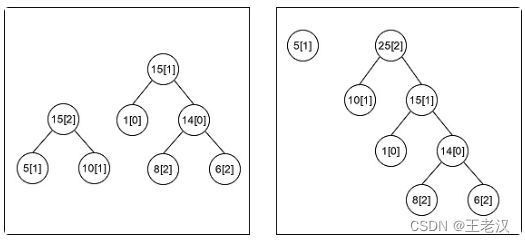
上图显示了两种不同的合并方式。其中节点中标明了每一堆的石子数目, 在方括号中标注了当前堆石子的颜色属性。左图的这种合并方式最终剩下了两 堆石子,所产生的合并总花费为 15 + 14 + 15 = 44;右图的这种合并方式最终 也剩下了两堆石子,但产生的合并总花费为 14 + 15 + 25 = 54。综上所述,我 们选择合并花费为 44 的这种方式作为答案。
【评测用例规模与约定】
对于 30% 的评测用例,1 ≤ N ≤ 10。
对于 50% 的评测用例,1 ≤ N ≤ 50。
对于 100% 的评测用例,1 ≤ N ≤ 300, 1 ≤ 每堆石子的数目 ≤ 1000。
【解题思路】
这题是在基础的合并石子动态规划问题上多了一个颜色转换的问题,需要考虑在i到j之间能否合并出一堆颜色为所标记的一堆,详细步骤看代码注释
【代码】
package zhenti_2023_hebingshizi;
import java.util.Scanner;
//1:无需package
//2: 类名必须Main, 不可修改
public class Main {
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
// 在此输入您的代码...
int N = scan.nextInt();
int[][][] min_sums = new int[3][N + 1][N + 1];// 存放不同颜色left~right区间合并的最小值
int[][] mins = new int[N + 1][N + 1];// 存放left~right区间合并的最小值
int[] nums = new int[N + 1];// 接收石子数据
int[] sums = new int[N + 1];// 存放前n堆石子数的总和
int[] clrs = new int[N + 1];// 接收颜色数据
int[][] min_nums = new int[N + 1][N + 1];// 存放left~right区间合并的最少堆数
// 为各颜色左右任意两点内的区间合并最小值赋值为int的最大值
for (int i = 1; i <= N; i++) {
for (int j = i; j <= N; j++) {
min_sums[0][i][j] = Integer.MAX_VALUE;
min_sums[1][i][j] = Integer.MAX_VALUE;
min_sums[2][i][j] = Integer.MAX_VALUE;
}
}
// 接收石子数目,并为sums赋值
for (int i = 1; i <= N; i++) {
nums[i] = scan.nextInt();
sums[i] = sums[i - 1] + nums[i];
}
// 接收颜色数据,并为石堆与自己合并值为0
for (int i = 1; i <= N; i++) {
clrs[i] = scan.nextInt();
min_sums[clrs[i]][i][i] = 0;
}
// 为区间最小堆数初始化赋值为原有堆数
for (int i = 1; i <= N; i++) {
for (int j = i; j <= N; j++) {
min_nums[i][j] = j - i + 1;
}
}
// len为区间长度
for (int len = 2; len <= N; len++) {
for (int left = 1; left <= N - len + 1; left++) {
// 利用左端点和区间长度求得右端点
int right = left + len - 1;
for (int k = left; k < right; k++) {
// 合并前的颜色clr_a
for (int clr_a = 0; clr_a < 3; clr_a++) {
int clr_l = (clr_a + 1) % 3;// 合并后的颜色clr_l
// 当dp[i][k]与dp[i+k][j]存在有效值时,dp[i][j]有值,进行对比赋值操作
// dp[i][j]=min(dp[i][j],dp[i][k]+dp[i+k][j]+(sum[j]-sum[i-1]))
// dp为区间合并最小石子数,i为左端点,j为右端点,k区间为i<=k
// sum为前n堆石子的和,则sum[j]-sum[i-1]为j~i区间石子的和
if (min_sums[clr_a][left][k] != Integer.MAX_VALUE
&& min_sums[clr_a][k + 1][right] != Integer.MAX_VALUE) {
min_sums[clr_l][left][right] = Math.min(min_sums[clr_l][left][right],
min_sums[clr_a][left][k] + min_sums[clr_a][k + 1][right]
+ (sums[right] - sums[left - 1]));
}
}
}
// 任一颜色的left~right区间有最小值,区间最少堆数为1,对区间合并后的最小值进行比对赋值,取最小
if (min_sums[0][left][right] != Integer.MAX_VALUE || min_sums[1][left][right] != Integer.MAX_VALUE
|| min_sums[2][left][right] != Integer.MAX_VALUE) {
min_nums[left][right] = 1;
mins[left][right] = Math.min(Math.min(min_sums[0][left][right], min_sums[1][left][right]),
min_sums[2][left][right]);
}
}
}
// 将最终结果进行比对,求得结果min_nums[1][N]、mins[1][N]
for (int left = 1; left <= N; left++) {
for (int k = left; k <= N; k++) {
for (int right = k + 1; right <= N; right++) {
// 当区间存在更小的堆数时,获取更小堆数,并存入与之对应的最小值
if (min_nums[left][right] > min_nums[left][k] + min_nums[k + 1][right]) {
min_nums[left][right] = min_nums[left][k] + min_nums[k + 1][right];
mins[left][right] = mins[left][k] + mins[k + 1][right];
} else if (min_nums[left][right] == min_nums[left][k] + min_nums[k + 1][right]) {
// 堆数相同时,获取更小的区间合并最小值
mins[left][right] = Math.min(mins[left][right], mins[left][k] + mins[k + 1][right]);
}
}
}
}
// 最终1~N区间的最小堆数与最小值为所求结果
System.out.println(min_nums[1][N] + " " + mins[1][N]);
scan.close();
}
}
试题 I: 最大开支
时间限制: 2.0s 内存限制: 512.0MB 本题总分:25 分
【问题描述】
小蓝所在学校周边新开业了一家游乐园,小蓝作为班长,打算组织大家去 游乐园玩。已知一共有 N 个人参加这次活动,游乐园有 M 个娱乐项目,每个 项目都需要买门票后才可进去游玩。门票的价格并不是固定的,团购的人越多 单价越便宜,当团购的人数大于某个阈值时,这些团购的人便可以免费进入项 目进行游玩。这 M 个娱乐项目是独立的,所以只有选择了同一个项目的人才可 以参与这个项目的团购。第 i 个项目的门票价格 Hi 与团购的人数 X 的关系可 以看作是一个函数:
Hi(X) = max(Ki × X + Bi , 0)
max 表示取二者之中的最大值。当 Hi = 0 时说明团购人数达到了此项目的 免单阈值。 这 N 个人可以根据自己的喜好选择 M 个娱乐项目中的一种,或者有些人 对这些娱乐项目都没有兴趣,也可以选择不去任何一个项目。每个人最多只会 选择一个娱乐项目,如果多个人选择了同一个娱乐项目,那么他们都将享受对 应的团购价格。小蓝想知道他至少需要准备多少钱,使得无论大家如何选择, 他都有能力支付得起所有 N 个人购买娱乐项目的门票钱。
【输入格式】
第一行两个整数 N、M,分别表示参加活动的人数和娱乐项目的个数。 接下来 M 行,每行两个整数,其中第 i 行为 Ki、Bi,表示第 i 个游乐地点 的门票函数中的参数。
【输出格式】
一个整数,表示小蓝至少需要准备多少钱,使得大家无论如何选择项目, 自己都支付得起。
【样例输入】
4 2
-4 10
-2 7
【样例输出】
12
【样例说明】
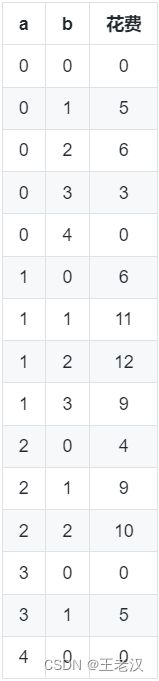
样例中有 4 个人,2 个娱乐项目,我们用一个二元组 (a, b) 表示 a 个人选 择了第一个娱乐项目,b 个人选择了第二个娱乐项目,那么就有 4 − a − b 个 人没有选择任何项目,方案 (a, b) 对应的门票花费为 max(−4 × a + 10, 0) × a + max(−2 × b + 7, 0) × b,所有的可能如下所示:
其中当 a = 1, b = 2 时花费最大,为 12。此时 1 个人去第一个项目,所以第一个项目的单价为 10 − 4 = 6,在这个项目上的花费为 6 × 1 = 6;2 个人去 第二个项目,所以第二个项目得单价为 7 − 2 × 2 = 3,在这个项目上的花费为2 × 3 = 6;还有 1 个人没去任何项目,不用统计;总花费为 12,这是花费最大 的一种方案,所以答案为 12。
【评测用例规模与约定】
对于 30% 的评测用例,1 ≤ N, M ≤ 10。
对于 50% 的评测用例,1 ≤ N, M ≤ 1000。
对于 100% 的评测用例,1 ≤ N, M, Bi ≤ 1 0 5 10^5 105,− 1 0 5 10^5 105≤ Ki < 0。
【解题思路】
本题运用贪心算法,通过计算增加到当前人数与之前的总价变化量,分析结果情况为:人数越多,变化量越小,因此只需求得两个项目变化量最大的几个总价变化量和,即为最大花费(每个项目变化量最大的必然是只有一个人玩时),不明白的可以看我的代码注释
【代码】
package zhenti_2023_zuidakaizhi;
import java.util.PriorityQueue;
import java.util.Scanner;
//1:无需package
//2: 类名必须Main, 不可修改
public class Main {
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
// 在此输入您的代码...
Main m = new Main();
int N = scan.nextInt();
int M = scan.nextInt();
int[] K = new int[M];
int[] B = new int[M];
for (int i = 0; i < M; i++) {
K[i] = scan.nextInt();
B[i] = scan.nextInt();
}
PriorityQueue<Integer> pq = new PriorityQueue<Integer>();// 默认从小到大排序
// 获取M个娱乐项目不同人数的总价变化量
for (int i = 0; i < M; i++) {
for (int j = 1; j <= N; j++) {
// 当总价变化量有效时,存入优先队列pq
if (m.price_changes(K[i], B[i], j) > 0) {
// 最大值取负号为最小值
pq.offer(-m.price_changes(K[i], B[i], j));
} else {
break;
}
}
}
int num = Math.min(pq.size(), N);// 取得最终游玩人数
long sum = 0;
// 取前num个最大变化量,即为最终解
for (int i = 0; i < num; i++) {
sum += (-pq.poll());
}
System.out.println(sum);
scan.close();
}
/**
* 计算增加到当前人数与之前的总价变化量
*
* !!!通过分析题目可知,人数越多,变化量越小!!!
*
* @param K 系数K
* @param B 系数B
* @param X 人数
* @return 人数变化量
*/
public int price_changes(int K, int B, int X) {
int change;
change = Math.max(X * (K * X + B) - (X - 1) * (K * (X - 1) + B), 0);
return change;
}
}
试题 J: 魔法阵
时间限制: 2.0s 内存限制: 512.0MB 本题总分:25 分
【问题描述】
魔法师小蓝为了营救自己的朋友小 Q,来到了敌人布置的魔法阵。魔法阵 可以看作是一幅具有 N 个结点 M 条边的无向图,结点编号为 0, 1, 2, . . . , N − 1, 图中没有重边和自环。敌人在每条边上都布置了陷阱,每条边都有一个伤害属 性 w,每当小蓝经过一条边时就会受到这条边对应的 w 的伤害。小蓝从结点 0出发,沿着边行走,想要到达结点 N − 1 营救小 Q。
小蓝有一种特殊的魔法可以使用,假设一条路径按照顺序依次经过了以下L 条边:e1, e2, . . . , eL(可以出现重复的边),那么期间小蓝受到的总伤害就是P = ∑L i=1 w(ei),w(ei) 表示边 ei 的伤害属性。如果 L ≥ K,那么小蓝就可以从 这 L 条边当中选出连续出现的 K 条边 ec , ec+1, . . . , ec+K−1 并免去在这 K 条边行 走期间所受到的伤害,即使用魔法之后路径总伤害变为 P ′ = P − ∑ i = c c + K − 1 \sum_{i=c}^{c+K−1} ∑i=cc+K−1 w(ei)。 注意必须恰好选出连续出现的 K 条边,所以当 L < K 时无法使用魔法。
小蓝最多只可以使用一次上述的魔法,请问从结点 0 出发到结点 N − 1 受 到的最小伤害是多少?题目保证至少存在一条从结点 0 到 N − 1 的路径。
【输入格式】
第一行输入三个整数,N, K, M,用空格分隔。 接下来 M 行,每行包含三个整数 u, v,w,表示结点 u 与结点 v 之间存在一 条伤害属性为 w 的无向边。
【输出格式】
输出一行,包含一个整数,表示小蓝从结点 0 到结点 N − 1 受到的最小伤 害。
【样例输入 1】
4 2 3
0 1 2
1 2 1
2 3 4
【样例输出 1】
2
【样例输入 2】
2 5 1
0 1 1
【样例输出 2】
0
【样例说明】
样例 1,存在路径:0 → 1 → 2 → 3,K = 2,如果在 0 → 1 → 2 上使用魔 法,那么答案就是 0 + 0 + 4 = 4;如果在 1 → 2 → 3 上使用魔法,那么答案就 是 2 + 0 + 0 = 2。再也找不到比 2 还小的答案了,所以答案就是 2。
样例 2,存在路径:0 → 1 → 0 → 1 → 0 → 1,K = 5,这条路径总计恰好 走了 5 条边,所以正好可以用魔法消除所有伤害,答案是 0。
【评测用例规模与约定】
对于 30% 的评测用例,1 ≤ N ≤ 20。
对于 50% 的评测用例,1 ≤ N ≤ 100。
对于 100% 的评测用例,1 ≤ N ≤ 1000, 1 ≤ M ≤ N×(N−1)/2 ,1 ≤ K ≤ 10, 0 ≤ u, v ≤ N − 1,1 ≤ w ≤ 1000。
【解题思路】
先通过dijkstra算法求得起点到终点的最小伤害(最短路径),再通过关系式子dp[y][j] = dp[x][j - 1]逐步求得使用魔法后的最小伤害,最后比对不使用魔法与使用魔法的最小伤害,输出最小值。
【代码】
package zhenti_2023_mofazhen;
import java.util.Vector;
import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;
//1:无需package
//2: 类名必须Main, 不可修改
public class Main {
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
// 在此输入您的代码...
Main ma = new Main();
int n = scan.nextInt();
int k = scan.nextInt();
int m = scan.nextInt();
// 创建一个动态扩容的存储空间ve,该存储空间存放着 动态扩容存放node的空间 的数据类型
Vector<Vector<node>> ve = new Vector<Vector<node>>();
// 根据结点数n传入n个数据类型为node的动态存储空间
for (int i = 0; i < n; i++)
ve.add(new Vector<node>());
// 获取各行对应的u、v、w,并存入对应的node数据(无向图可双向前进,即u可到v,v可到u)
for (int i = 1; i <= m; i++) {
int u = scan.nextInt();
int v = scan.nextInt();
int w = scan.nextInt();
ve.get(u).add(new node(v, w));
ve.get(v).add(new node(u, w));
}
System.out.println(ma.dij(ve, n, k));
scan.close();
}
// 结点对象
static class node {
// 可前往的结点
int to;
// 到to这个结点受到的的伤害
int w;
// 构造方法
public node(int a, int b) {
to = a;
w = b;
}
}
// 运用Dijkstra、Dp算法进行求解
public int dij(Vector<Vector<node>> ve, int n, int k) {
// 创建一个运用dp算法的二维数组d,dp[i][j]表示从0跑到i,且消除j条连续边伤害的最小伤害。
int dp[][] = new int[1001][11];
// 为dp中的每个数据初始化为一个较大值,不能为int最大值,后面比较会超出范围
for (int i = 0; i < n; i++)
for (int j = 0; j <= k; j++)
dp[i][j] = (int) 1e9;
// 不使用魔法且到达出发点,受到的最小伤害为0
dp[0][0] = 0;
// 创建队列q存储类型为integer
Queue<Integer> q = new LinkedList<Integer>();
// 将出发点入队
q.add(0);
// 当队列不为空时继续循环,为空退出循环
while (!q.isEmpty()) {
// 将队头出队,且赋值给x
// 利用队列先入先出原则,从头结点一步步往目标结点比对,实现Dijkstra算法
int x = q.poll();
// 逐一获取x对应的动态存储空间内的node进行操作
for (node o : ve.get(x)) {
// 获取当前node中的to、w,对y、w进行赋值
int y = o.to, w = o.w;
// 判断是否进行过操作,默认false
boolean f = false;
// 不使用魔法,0到y有比原先更小伤害(即0到y最短路径),进行赋值操作,f改为true
if (dp[y][0] > dp[x][0] + w) {
dp[y][0] = dp[x][0] + w;
f = true;
}
// 得到公式dp[y][j]=dp[x][j-1]
// 使用魔法j,0到y有比原先更小伤害,进行赋值操作,f改为true
for (int j = 1; j <= k; j++) {
if (dp[y][j] > dp[x][j - 1]) {
dp[y][j] = dp[x][j - 1];
f = true;
}
}
// 使用题目给定魔法k,0到y有比原先更小伤害,进行赋值操作,f改为true
if (dp[y][k] > dp[x][k] + w) {
dp[y][k] = dp[x][k] + w;
f = true;
}
// 当进行过操作时,将下一结点下标y入队
if (f)
q.add(y);
}
}
return Math.min(dp[n - 1][0], dp[n - 1][k]);
}
}