盘点一些著名的树型结构习题和图的分类

在前面学过的存放数据的容器有：数组、链表、栈、队列等，这些都是线性结构，数据元素之间存在一对一的线性关系。但在实际生活中，往往是非线性关系，数据元素之间的关系通常可以一对多。所以必须要把这些数据关系储存下来：

—.树的概念

树形结构

树的初始起点：我们定义为根。

递归树中，都只能从父节点走到子节点。

我们只需要记录每个父节点有哪些子节点，那么就可以遍历整个递归树。

我们可以用动态数组(vector)来记录每个节点的子节点。这就是树的孩子表示法

---

1.根节点：最顶层的节点就是根结点，它是整棵树的源头，一般用root表示。

2.叶子节点：在树最底端的节点，就是其子节点个数为0的节点

3.叶子节点：5，6，7，9，10节点的度：指定节点有子节点的个数。节点3的度为2。

4.树的度：只看根结点，树的度等价于根节点的度。例如根节点的度为3，因此树的度为3

5.无根树：没有指定根节点的树，树的形态多样。明显这里以1为根和以5为根，树的形态不一样。

6.有根树：指定了根节点的树，树的形态唯一。

7.森林：由多棵树构成

例12.1-1 树的统计

描述

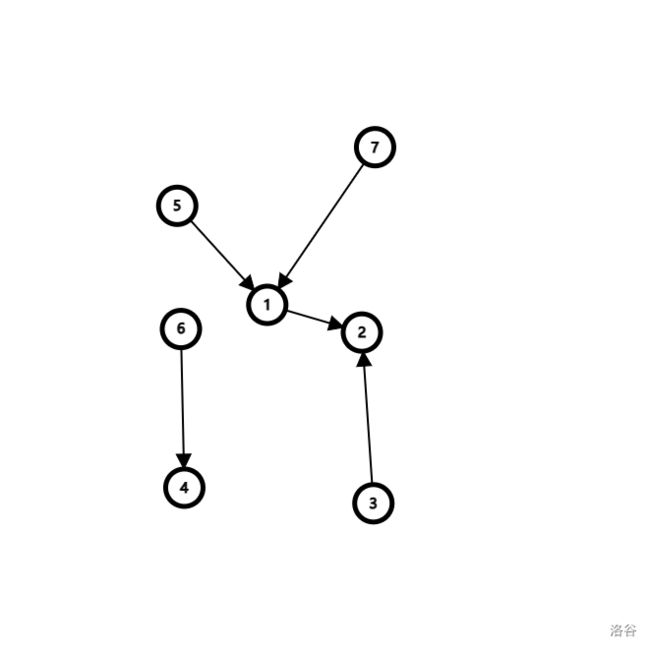
输入森林中的结点关系，统计森林中树的数量，输出树的根。

输入描述

第一行：n：结点数量；k：边数；（n,k<=100）

以下k行：每行两个结点编号：i，j：i是j的父结点(I,j<=100)。

输出描述

第一行：树的数量。
第二行：依次输出森林中树的根结点编号（从小到大）。

#include
using namespace std;
int fa[1010];
int main(){
	int n,k;
    cin>>n>>k;
    for(int i=0;i<k;i++){
        int x,y;
        cin>>x>>y;
        fa[y]=x;
    }
    cout<<n-k<<endl;
    for(int i=1;i<=n;i++){
        if(fa[i]==0) cout<<i<<" ";//根节点的父亲为0
    }
	return 0;
}

这道题通过简单的树状存储，实现了查找等功能…

当然，我提倡用vector来代替int,这样不会浪费过多的空间

---

例12.1-2 找树根和孩子

描述

给定一棵树，输出树的根root，孩子最多的结点max（该节点保证唯一）以及他的孩子.

输入描述

第一行：n（结点个数≤100），m（边数≤200）。

以下m行：每行两个结点x和y，表示y是x的孩子(x,y≤1000)。

输出描述

第一行：树根：root；
第二行：孩子最多的结点max；
第三行：max的孩子（按编号由小到大输出）。

#include
using namespace std;
int fa[1010];
vector <int> ms[1001];
int main(){
	int n,m;
    cin>>n>>m;
    for(int i=0;i<m;i++){
        int x,y;
        cin>>x>>y;
        fa[y]=x;
        ms[x].push_back(y);
    }
    for(int i=1;i<=n;i++){
        if(fa[i]==0) cout<<i<<endl;
    }
    int max,sh;
	for(int i=1;i<=n;i++){
        if(max<ms[i].size()){
            sh=i;
            max=ms[i].size();
        }
    }//和例1几乎一样
    cout<<sh<<endl;
    for(int i=0;i<ms[sh].size();i++){
        cout<<ms[sh][i]<<" ";
    }
	return 0;
}

这一颗有向的树形结构。

如上

我建立fa[1010]记录父亲从而找到根节点。使用vector将每个节点的子节点进行存储，最后遍历找到哪个节点的子节点最多，输出即可。

---

前两道例题都是有向的边，所以不担心会从子节点重新走到父亲节点。

但是通常来讲，树的边都是双向的,我们在遍历的时候不希望一个点遍历多次。

那有什么办法呢？

这时我突然想起了想起dfs()

方法1. 用bool数组进行标记。

方法2. dfs()中记录由父亲节点，这样可以阻止走回去。

---

所以按照以上的思路,下面的那道题不就是轻轻松松吗?

例12.1-3 树的遍历

描述

给定一棵树，默认根节点为编号为1号的那一个节点，输出树的深度优先遍历结果。

输入描述

第一行：n（结点个数≤100），m（边数≤200）。

第二行为：n个结点，从编号1~n 每个结点存放的数据。

以下m行：每行两个结点编号x和y，表示x与y相连(x,y≤1000)

注意：先连的边先输出。

输出描述

一行，数据域的遍历结果，空格隔开。

#include
using namespace std;
int fa[1010];
int a[10001];
vector <int> w[1001];
void dfs(int n,int f){
    cout<<a[n]<<" ";
    for(int i=0;i<w[n].size();i++){
        int y=w[n][i];
        if(y==f) continue;
        dfs(y,n);
    }
}

int main(){
    int n,k;
    cin>>n>>k;
    for(int i=1;i<=n;i++){
        cin>>a[i];
    }
    for(int i=0;i<k;i++){
        int x,y;
        cin>>x>>y;
        w[x].push_back(y);
        w[y].push_back(x);
    }
    dfs(1,0);
	return 0;
}

与上一题不同，本题 未说明 父子关系，是一颗普通树(双向)。

所以存放当前节点的子节点时，需要特别注意只要某个节点与当前节点相连，都可视为它的子节点。

我从根节点出发，为了不重复遍历，可以在dfs中带入父亲节点编号，从而防止再次访问到父节点。

---

例12.1-4 最大链长

描述

给定一棵有n个点的树（结点个数≤100），指定根节点为1.

输入描述

第一行为n.

后面n-1行，每行三个数a,b,c，分别表示节点a,b之间存在边，边权为c.(1<=a,b,c<=n)

输出描述

输出距离根的最大链长，以及最大链长数目

#include
using namespace std;
vector <int> fa[10001];
vector <int> coin[10001];
int discoin[1001];//累计
void dfs(int x,int f){
    for(int i=0;i<fa[x].size();i++){
        int ch=fa[x][i];
        if(f==ch) continue;
        discoin[ch]=discoin[x]+coin[x][i];
        dfs(ch,x);
    }
}
int maxn=0,cnt=0;
int main(){
	int n;
    cin>>n;
    for(int i=1;i<n;i++){
        int x,y,z;
        cin>>x>>y>>z;
        fa[x].push_back(y);
        coin[x].push_back(z);
        fa[y].push_back(x);//没有指定方向
        coin[y].push_back(z);//边权
    }
 	dfs(1,0);
    
    for(int i=1;i<=n;i++) maxn=max(maxn,discoin[i]);//求最大值
    for(int i=1;i<=n;i++) if(discoin[i]==maxn) cnt++;//个数
    cout<<maxn<<" "<<cnt;
	return 0;
}

---

这是一道简单的模板题，通过性质：任意点的最长链端点一定是直径端点来求解

这道题可以先用dfs求出每个点与根的距离，找到最大值maxn，再看有几个点的距离为maxn

我随意找一个点x,进行dfs找到最长链的端点s,再以端点s做第二遍dfs，此时可以找到直径的第二个端点t。

此时端点s到t的距离就是树的直径

---

练12.1-7 树的分解

二.树的直径及其性质

描述

给出 N 个点的树和K，问能否把树划分成 N/K

个连通块，且每个连通块的点数都是 K。

输入描述

第一行，一个整数 T，表示数据组数。接下来 T 组数据，对于每组数据：

第一行，两个整数 N,K。

接下来 N−1 行，每行两个整数 Ai,Bi ，表示边 (Ai,Bi)。点用 1,2,…,N 编号。

输出描述

对于每组数据，输出 YES 或NO。

#include
#pragma GCC target("avx")
#pragma GCC optimize(2)
#pragma GCC optimize(3, "Ofast", "inline")
#pragma GCC optimize("-fcse-skip-blocks")
#pragma GCC optimize("-fcse-follow-jumps")
#pragma GCC optimize("-fsched-interblock")
#pragma GCC optimize("-fpartial-inlining")
using namespace std;
const int N=1e5+10,M=N*2;
int n,k;
int h[N],e[M],ne[M],idx,cnt;
int st[N];
void add(int a,int b){e[idx]=b,ne[idx]=h[a],h[a]=idx++;}
void dfs(int x,int s)
{
    st[x]=1;
    for(int i=h[x];~i;i=ne[i])
    {
        int j=e[i];
        if(j!=s)
        {
            dfs(j,x);
            st[x]+=st[j];
        }
    }   
    if(st[x]==k){st[x]=0;cnt++;}  
}
int main()
{
	ios::sync_with_stdio(false);
    cin.tie(0);
    int t;
    scanf("%d",&t);
    while(t--)
    {
        int a,b;
        memset(h,-1,sizeof h);
        memset(st,0,sizeof st);
        idx=0;cnt=0;
        scanf("%d%d",&n,&k);
        for(int i=1;i<n;i++)
        {
            scanf("%d%d",&a,&b);
            add(a,b),add(b,a);
        }
        if(n%k!=0){puts("NO");continue;}
        dfs(1,0);
        if(cnt==n/k) puts("YES");
        else puts("NO");
    }
    return 0;
}

这道题通过特判和路径压缩,不断地更新节点的父亲节点,将树不断地分割,代码原理很简单.

例12.2-1 树的直径

#include
using namespace std;
vector <int> fa[10001];
vector <int> coin[10001];
int discoin[10001];//累计
int maxele=0,s;
void dfs(int x,int f){
    for(int i=0;i<fa[x].size();i++){
        int ch=fa[x][i];
        if(f==ch) continue;
        discoin[ch]=discoin[x]+coin[x][i];
        if(discoin[ch]>maxele) maxele=discoin[ch],s=ch;
        dfs(ch,x);
    }
}
int main(){
	int n;
    cin>>n;
    for(int i=0;i<n;i++){
        int x,y,z;
        cin>>x>>y>>z;
        fa[x].push_back(y);coin[x].push_back(z);
        fa[y].push_back(x);coin[y].push_back(z);
    }
    dfs(1,0);
    memset(discoin,0,sizeof discoin);
    maxele=0;
    dfs(s,0);
    cout<<maxele;
	return 0;
}

其实这道题和最大链长一模一样[doge].

---

例12.2-2 左右端点距离

描述

输入一颗无根树，输出各个点到左右端点的距离。(默认左端点为编号小的点，右端点为编号大的点。)

输入描述

第一行为一个正整数n,表示这颗树有n个节点

接下来的n−1行,每行三个正整数u,v,w，表示u,v（u,v<=n）有一条权值为w的边相连

输出描述

输入有n行，每行三个数字，分别表示节点编号,到左端点距离与到右端点距离。

#include
using namespace std;
vector <int> fa[10001];
vector <int> coin[10001];
int discoin[10001];//累计
int try_;
int maxele=0,s;
int ld[114514],rd[114514];
int lp,rp;
void dfs(int x,int f,int cnt){
    for(int i=fa[x].size()-1;i>=0;i--){
        int ch=fa[x][i];
        if(f==ch) continue;
        discoin[ch]=discoin[x]+coin[x][i];
        if(discoin[ch]>maxele) maxele=discoin[ch],try_=ch;
        if(cnt==2) ld[ch]=discoin[ch];//
        if(cnt==3) rd[ch]=discoin[ch];//
        dfs(ch,x,cnt);
        
    }
}
int main(){
	int n;
    cin>>n;
    for(int i=1;i<n;i++){
        int x,y,z;
        cin>>x>>y>>z;
        fa[x].push_back(y);coin[x].push_back(z);
        fa[y].push_back(x);coin[y].push_back(z);
    }
    try_=1;
    for(int i=1;i<=3;i++){
        maxele=0;
        memset(discoin,0,sizeof discoin);
        dfs(try_,0,i);
        if(i==1) lp=try_;
        if(i==2) rp=try_;
    }
    if(rp>lp) swap(rd,ld);//左端点小于右端点
    for(int i=1;i<=n;i++){
        cout<<i<<" "<<rd[i]<<" "<<ld[i]<<endl;;
    }
	return 0;
}

这道题和上道题一样，只是要加两个数组来存储此节点距离左端点和右端点的长度。

---

例12.2-3 树的中心

描述

给定一棵树，树中包含 n个结点（编号1~n）和 n−1 条无向边，每条边都有一个权值。

请你在树中找到一个点，使得该点到树中其他结点的最远距离最近。

输入描述

第一行包含整数 n。

接下来 n−1行，每行包含三个整数 ai,bi,ci，表示点 ai 和 bi 之间存在一条权值为 ci 的边。

输出描述

输出两个整数，第一个整数表示树的中心的节点编号，第二个整数表示所求点到树中其他结点的最远距离。(如果存在两个中心，则输出节点编号较小的一个）

#include
using namespace std;
vector <int> fa[10001];
vector <int> coin[10001];
int discoin[10001];//累计
int try_;
int maxele=0,s;
int maxn=INT_MAX;
int lp,rp;
int dis[10001];
void dfs(int x,int f,int cnt){
    for(int i=fa[x].size()-1;i>=0;i--){
        int ch=fa[x][i];
        if(f==ch) continue;
        discoin[ch]=discoin[x]+coin[x][i];
        dis[ch]=max(dis[ch],discoin[ch]);
        if(cnt==3) maxn=min(maxn,dis[ch]);
        if(discoin[ch]>maxele) maxele=discoin[ch],try_=ch;
        dfs(ch,x,cnt);
        
    }
}
int main(){
	int n;
    cin>>n;
    for(int i=1;i<n;i++){
        int x,y,z;
        cin>>x>>y>>z;
        fa[x].push_back(y);
        coin[x].push_back(z);
        fa[y].push_back(x);
        coin[y].push_back(z);
    }
    try_=1;
    for(int i=1;i<=3;i++){
        maxele=0;
        memset(discoin,0,sizeof discoin);
        dfs(try_,0,i);
    }
    for(int i=1;i<=n;i++){
        if(dis[i]==maxn){ cout<<i<<" "<<maxn;break;}
    }
	return 0;
}

---

数组表述每个点出发的最大距离，因此我们在第2次和第3次dfs的过程中，与dis数组比较即可。并且在第3次dfs时，把最小距离求出来

---

三.树的重心及其性质

使得最大子树大小最小。那么这个点叫就被叫做树的重心

例12.3-1 找出树的重心

描述

给定一个n(n<=1e5)个点的树，找出树的重心(重心不止一个，则输出编号较小的那个)，以及当前重心下的最大子树大小。

输入描述

第一行一个数字n

第二行n-1个数字，表示两点之间存在一条边相连

输出描述

按要求输出两个整数，用空格隔开

#include
using namespace std;
const int N=1e5+5;
int n;
vector <int > v[N];
int sz[N]; 
int lop=N;
int lol;
int dfs(int x,int fa){
    sz[x]=1;
    int maxn=0;
    for(int i=0;i<v[x].size();i++){
        int m=v[x][i];
        if(m==fa) continue;
        dfs(m,x);
        sz[x]+=sz[m];
        maxn=max(maxn,sz[m]);
    }
    maxn=max(maxn,n-sz[x]);
     if(lop>maxn) lop=maxn,lol=x;
    else if(lop==maxn && lol>x) lol=x;
    return lol;
}
int main(){
    cin>>n;
    for(int i=1;i<n;i++){
        int x,y;
        cin>>x>>y;
        v[x].push_back(y);
        v[y].push_back(x);
    }
    dfs(1,0);
    cout<<lol<<" "<<lop;
	return 0;
}

显然，要求树的重心，我枚举出每个点为断点时，所产生的最大子树大小。

某断点求当前最大子树大小的方法： 对该点进行dfs，找到以i为根节点的子树的大小记录到sz[i]中，接着在该点的儿子中

找sz[i]最大的一个。复杂度为O(n2)

十分简单对吧[doge]

但我又在下一题中被啪啪打脸了。

---

例12.3-2 子树的重心

描述

输入一棵树,判断每一棵子树的重心是哪一个节点。

输入描述

第一行输入n,q。n表示树的节点个数，q表示询问次数

第二行n-1个数，分别表示从节点2开始，各节点的父亲节点。

后面q行，每行一个数x，表示询问当前以x为根的子树中，树的重心位置。

输出描述

q行，每行表示一个答案

#include
using namespace std;
#pragma once
#pragma GCC diagnostic error "-std=c++11"
#pragma GCC target("avx")
#pragma GCC optimize(2)
#pragma GCC optimize(3, "Ofast", "inline")
#pragma GCC optimize("Ofast")
#pragma GCC optimize("inline")
#pragma GCC optimize("-fgcse")
#pragma GCC optimize("-fgcse-lm")
#pragma GCC optimize("-fipa-sra")
#pragma GCC optimize("-ftree-pre")
int fa[10000000];
vector <int> v[10000001];
int n,m;
#define int long long
int tp[111110100],sz[100000001],id[10000000];
inline void dfs(int x){
    sz[x]=1;
    for(int i=0;i<v[x].size();i++){
        int ch=v[x][i];
        dfs(ch);
        sz[x]+=sz[ch];
        if(sz[ch]>sz[id[x]]) id[x]=ch;
    }
    if(id[x]==0){
        tp[x]=x;
        return;
    }
    tp[x]=tp[id[x]];
    while(sz[tp[x]]*2<sz[x]) tp[x]=fa[tp[x]];
}
signed main(){
    scanf("%d %d",&n,&m);
    for(register int i=2;i<=n;i++){
        int x;
        scanf("%lld",&x);
        fa[i]=x;
        v[x].push_back(i);
    }
    dfs(1);
    for(register int i=1;i<=m;i++){
        int x;
        scanf("%lld",&x);
        cout<<tp[x]<<endl;;
    }
}

@我差点没看懂题@
开了一大堆的优化才勉强没TLE

本题若对每一次询问都查询一遍子树的重心，那么复杂度为O(nq)。

在我们求一颗树T的重心时，根据中心公理知道，重心一定在最大子树的重心到该树的根这一条链上.

所以我们如果知道最大子树的重心，

此时就可以遍历这一条链上的点，

只要该点满足其最大子树大小不超过n/2，那么一定是重心。

所以我们可以dfs下去，先求出小的子树重心，回溯时再把当前的重心进行记录即可。复杂度O(n+q)

---

现在来科普几个重心的性质

1. 重心点的最大子树大小不大于整棵树大小的一半。

2.非空树有且仅有1-2个重心。

3.树中所有点到重心的距离和最小，反过来距离和最小的点一定是重心.

---

四.树的集合性质与并查集

1.树的集合性质

//树具备连通性
//我们可以将一棵树当成一个集合，
//集合中的元素就是树上的节点。
//在树中的任意两点，也就是集合内部的两个元素一定能相互连通。
//此时若要查询两点是否属于同一个集合，只需要查询两点是否连通即可。

例12.4-1 团队关系

描述

有n个人，m条两两关系，组成若干个团队，保证每个团队都是一个树形结构，给出q个询问，对于每个询问进行回答(n,q<=1e5,m<n)。

输入描述

第一行输入n,m,q

随后m行，每行输入a,b表示a与b是一个团队
。
最后q行，每行输入两个数c,d，如果c,d属于一个团队，则输出YES,否则输出NO。

输出描述

q行，每一行表示一个答案。

#include
using namespace std;
const int N=1E5+5;
vector <int> v[N];
int p[N];
int n,m,q;
void dfs(int x,int fa,int idx){
    p[x]=idx;
    for(int i=0;i<v[x].size();i++){
        int y=v[x][i];
        if(y==fa) continue;
		dfs(y,x,idx);
    }
}
int main(){
    cin>>n>>m>>q;
    for(int i=1;i<=m;i++) {
        int x,y;
        cin>>x>>y;
        v[x].push_back(y);
        v[y].push_back(x);
    }
    for(int i=1;i<=n;i++){
        if(p[i]==0) dfs(i,0,i);
        
    }
    for(int i=0;i<q;i++){
        int x,y;
        cin>>x>>y;
        if(p[x]==p[y]) cout<<"YES\n";
        else cout<<"NO\n";
    }
	return 0;
}

数据范围较大，显然不能询问一次就进行一次dfs。

这道题我通过更新子节点的父亲为根节点，时间复杂度降为O(n+q)

我的想法类似于这样:

---

例12.4-2 并查集操作

描述

如题，现在有一个并查集，你需要完成合并和查询操作。

输入描述

第一行包含两个整数 N,M ,表示共有 N 个元素和 M个操作。

接下来 M 行，每行包含三个整数 Zi ,Xi ,Yi 。

当 Zi=1 时将Xi与Yi所在的集合合并。

当 Zi=2 时，输出 Xi与Yi是否在同一集合内，是的输出 Y ；否则输出 N 。

输出描述

对于每一个 Zi=2 的操作，都有一行输出，每行包含一个大写字母，为 Y 或者 N。

#include
using namespace std;
const int N=1E5+5;
int fa[N];
int p[N];
int n,m,q;
int ask(int x){
    if(x==fa[x]) return x;
    return fa[x]=ask(fa[x]);
}
int main(){
    cin>>n>>m;
    for(int i=1;i<=n;i++) fa[i]=i;
    while(m--){
        int z,x,y;
        cin>>z>>x>>y;
        int i=ask(x),j=ask(y);
        if(z==1){
            if(i==j) continue;
            fa[i]=j;
        }
        if(z==2){
            if(i==j) cout<<"Y\n";
            else cout<<"N\n";
        }
    }
}

这道题不仅和上一道题几乎一摸一样,居然还是到模板题

但却需要一点优化

现在我要来说说并查集的两个优化方式

---

1.路径压缩优化

这个和我刚才讲的是一个东西

只要给ask()加一个记忆化就行了

这样可以保证，每个点遍历一次后，他们就一定直接连到树根上。再查询x树根时，可以很轻松获得。

---

2.按秩合并优化

路径压缩能起到非常好的优化效果，但是破坏了原树的形态。

优化的核心点是在于降低树的高度，使得查询根节点更快。那我们在合并时注意到，每次合并树的高度有可能增加非常多。

如果降低合并两颗树的新树高，也能起到优化作用。这个思想就是按秩合并(秩：树高)

我们只需要用一个merge()将原树高与新树高融合

---

例12.4-3 银河英雄传说

描述

公元 5801 年，地球居民迁至金牛座 α 第二行星，在那里发表银河联邦创立宣言，同年改元为宇宙历元年，并开始向银河系深处拓展。

宇宙历 799 年，银河系的两大军事集团在巴米利恩星域爆发战争。泰山压顶集团派宇宙舰队司令莱因哈特率领十万余艘战舰出征，气吞山河集团点名将杨威利组织麾下三万艘战舰迎敌。

杨威利擅长排兵布阵，巧妙运用各种战术屡次以少胜多，难免恣生骄气。在这次决战中，他将巴米利恩星域战场划分成 30000 列，每列依次编号为 1,2,…,30000。之后，他把自己的战舰也依次编号为 1,2,…,30000，让第 i 号战舰处于第 i 列，形成“一字长蛇阵”，诱敌深入。这是初始阵形。当进犯之敌到达时，杨威利会多次发布合并指令，将大部分战舰集中在某几列上，实施密集攻击。合并指令为 M i j，含义为第 i 号战舰所在的整个战舰队列，作为一个整体（头在前尾在后）接至第 j 号战舰所在的战舰队列的尾部。显然战舰队列是由处于同一列的一个或多个战舰组成的。合并指令的执行结果会使队列增大。

然而，老谋深算的莱因哈特早已在战略上取得了主动。在交战中，他可以通过庞大的情报网络随时监听杨威利的舰队调动指令。

在杨威利发布指令调动舰队的同时，莱因哈特为了及时了解当前杨威利的战舰分布情况，也会发出一些询问指令：C i j。该指令意思是，询问电脑，杨威利的第 i 号战舰与第 j 号战舰当前是否在同一列中，如果在同一列中，那么它们之间布置有多少战舰。

作为一个资深的高级程序设计员，你被要求编写程序分析杨威利的指令，以及回答莱因哈特的询问。

输入描述

第一行有一个整数 T(1≤T≤5×10e5),表示总共有 T 条指令。

以下有T 行，每行有一条指令。指令有两种格式：

M i j：i 和j 是两个整数（1≤i,j≤30000），表示指令涉及的战舰编号。该指令是莱因哈特窃听到的杨威利发布的舰队调动指令，并且保证第 i号战舰与第 j 号战舰不在同一列。

C i j：i 和 j 是两个整数（1≤i,j≤30000），表示指令涉及的战舰编号。该指令是莱因哈特发布的询问指令。

输出描述

依次对输入的每一条指令进行分析和处理：

如果是杨威利发布的舰队调动指令，则表示舰队排列发生了变化，你的程序要注意到这一点，但是不要输出任何信息。
如果是莱因哈特发布的询问指令，你的程序要输出一行，仅包含一个整数，表示在同一列上，第 i 号战舰与第 j 号战舰之间布置的战舰数目。如果第 i 号战舰与第 j 号战舰当前不在同一列上，则输出 −1。

#include
#pragma GCC diagnostic error "-std=c++11"
#pragma GCC target("avx")
#pragma GCC optimize(2)
using namespace std;
const int P=5e5+5;
int fa[P],sz[P];
int d[P];
int n;
int ask(int x){
    if(x==fa[x]) return x;
    int root=ask(fa[x]);
    d[x]+=d[fa[x]];
    return fa[x]=root;
}
void marge(int x,int y){
    x=ask(x),y=ask(y);
    fa[x]=y,d[x]=sz[y],sz[y]+=sz[x];
}
int main(){
    std::ios::sync_with_stdio(false);
	cin.tie(NULL); cout.tie(NULL);
	cin>>n;
    for(int i=1;i<=n;i++) fa[i]=i,sz[i]=1;
    while(n--){
        char ch;int x,y;
       	cin>>ch>>x>>y;
        if(ch=='M') marge(x,y);
        if(ch=='C'){
            int i=ask(x),j=ask(y);
            if(i!=j){
                cout<<-1<<endl;
                continue;
            }
            cout<<abs(d[x]-d[y])-1<<endl;
        }
        
    }
}

这道题前面一大堆的废话,绕来绕去

其实这道题十分简单

用数组d表示每个点到当前根节点的距离。那么：同一集合内i,j之间的战舰数量等于abs(d[i]-d[j])-1。

我们用并查集维护集合关系，由于数据范围较大，需要路径压缩优化，加快查询速度。

因此原有树形结构被破坏，我们还需要 维护任意到到根节点的距离不变 ，也就是数组d。

---

练12.4-5 找亲戚

描述

或许你并不知道，你的某个朋友是你的亲戚。他可能是你的曾祖父的外公的女婿的外甥女的表姐的孙子。
如果能得到完整的家谱，判断两个人是否是亲戚应该是可行的，但如果两个人的最近公共祖先与他们相隔好几代，使得家谱十分庞大，那么检验亲戚关系实非人力所能及。在这种情况下，最好的帮手就是计算机。
为了将问题简化，你将得到一些亲戚关系的信息，如Marry和Tom是亲戚，Tom和Ben是亲戚，等等。从这些信息中，你可以推出Marry和Ben是亲戚。
请写一个程序，对于我们的关于亲戚关系的提问，以最快的速度给出答案。

输入描述

输入由两部分组成。

第一部分以N,M开始.N为问题涉及的人的个数(1≤N≤2×10e4)。
这些人的编号为1,2,3,…,N。下面有M行(1≤M≤10e6)，每行有两个数ai,bi,表示已知ai和bi是亲戚。

第二部分以Q开始。表示有Q个询问(1≤Q≤10e6 )
每行为ci,di，表示询问ci和di是否为亲戚。

输出描述

对于每个询问ci,di，输出一行：若ci和di为亲戚，则输出Yes，否则输出NO。

#include
#pragma GCC target("avx")
#pragma GCC optimize(2)
#pragma GCC optimize(3, "Ofast", "inline")
#pragma GCC optimize("inline")
using namespace std;
int fa[20005];
int n,m,a,b,q,s,f;
char ch;
int read(){
    s=0,f=1;ch=getchar();
    while(!isdigit(ch)){if(ch=='-') f=-1;ch=getchar();}
    while(isdigit(ch)) s=s*10+ch-'0',ch=getchar();
    return s*f;
}
int ask(int x){
    if(x==fa[x]) return x;
    return fa[x]=ask(fa[x]);
}
int main(){
    n=read(),m=read();
    while(n--) fa[n]=n;
    while(m--) a=ask(read()),b=ask(read()),fa[a]=b;
    q=read();
    while(q--){
        a=ask(read()),b=ask(read());
        a==b?printf("Yes\n"):printf("No\n");
    }
    return 0;
}

并查集的模板非常简单，主要难点在于应用。我们知道，具有关系传递性质的题目我们都可以往树上思考。并查集在树的基础上进行升级，不仅可以维护一个集合，还可以维护集合中任意两点的关系。

这道题主要考的是对压缩树的熟练程度

但这道题也有找规律的成分在里面,所以我的代码十分精简

---

练12.4-6 犯罪团伙

描述

警察抓到了n个罪犯,警察根据经验知道他们属于不同的犯罪团伙,却不能判断有多少个团伙,但通过警察的审讯,知道其中的一些罪犯之间相互认识。

已知同一犯罪团伙的成员之间直接或间接认识。有可能一个犯罪团伙只有一个人。

请你根据已知罪犯之间的关系,确定犯罪团伙的数量。已知罪犯的编号从1至n。

输入描述

第一行：n(n<=1000,罪犯数量),
第二行：m(m<5000,关系数量)
以下若干行：每行两个数：I 和j,中间一个空格隔开,表示罪犯i和罪犯j相互认识。

输出描述

一个整数,犯罪团伙的数量

#include
#pragma GCC optimize(2)
using namespace std;
vector<int> v[100005];
int fa[100005];
int vis[100005];
int n,m,ans;
int ask(int x){
	if(x==fa[x])	return x;
	return fa[x]=ask(fa[x]);
}
int main(){
	cin>>n>>m;
	for(int i=1;i<=n;i++)	fa[i]=i;
	for(int i=1;i<=m;i++){
		int x,y;
		scanf("%d%d",&x,&y);
		int a=ask(x),b=ask(y);
		fa[a]=b;	
	}
	for(int i=2;i<=n;i++){
		int a=ask(1);
		int b=ask(i);
		vis[a]++;
		vis[b]++;
	}
	for(int i=1;i<=n;i++){
		if(vis[i]!=0)	ans++;
	}
	cout<<ans;
}

这道题我用的是路径压缩, 只要与根结点有关系，就把其设为根节点，再逐次枚举。

---

练12.4-7 朋友和敌人

描述

在某城市里住着n个人，任何两个认识的人不是朋友就是敌人，而且满足：

1、我朋友的朋友是我的朋友；

2、我敌人的敌人是我的朋友；

所有是朋友的人组成一个团伙。告诉你关于这n个人的m条信息，即某两个人是朋友，或者某两个人是敌人，请你编写一个程序，计算出这个城市最多可能有多少个团伙？

输入描述

第1行为n和m，1

以下m行，每行为p x y，p的值为0或1，p为0时，表示x和y是朋友，p为1时，表示x和y是敌人。

输出描述

一个整数，表示这n个人最多可能有几个团伙。

---

这道题我就先不展示代码了,但我说一下我的思路(其实上是我懒得再打一遍 )

先看一下这张图;

我的思路你们大概应该知道了吧(敌人的敌人是朋友)

---

五.二叉树的存储遍历和转化

二叉树是什么东东？

二叉树（binary tree,简写成BT）是一种特殊的树型结构，保证了每个结点最多有两个子结点。

每个结点的子结点分别称为左孩子、右孩子，它的两棵子树分别称为左子树、右子树

---

例12.5-1 二叉树遍历

描述

建立二叉树，然后实现：输出先序遍历、中序遍历、后序遍历的结果。

输入描述

第一行：结点个数n（n<=100)。

以下行：每行3个数，第一个是父亲，后两个依次为左右孩子，0表示空。

输出描述

三行分别为先、 中、后序 遍历结果

#include
using namespace std;
int rs[105],ls[105],fa[105];
int n;
void dfs1(int x){
    cout<<x<<" ";
    if(ls[x]) dfs1(ls[x]);
    if(rs[x]) dfs1(rs[x]);
}
void dfs2(int x){
    if(ls[x]) dfs2(ls[x]);
    cout<<x<<" ";
    if(rs[x]) dfs2(rs[x]);
    
}
void dfs3(int x){
    
    if(ls[x]) dfs3(ls[x]);
    if(rs[x]) dfs3(rs[x]);
    cout<<x<<" ";
}
int main(){
    cin>>n;
    for(int i=1;i<=n;i++){
        int x,y,z;
        cin>>x>>y>>z;
        ls[x]=y,rs[x]=z;
        fa[y]=x;
        fa[z]=x;
    }
    int root;
    for(int i=1;i<=n;i++) if(fa[i]==0) root=i;
    dfs1(root);cout<<"\n";
    dfs2(root);cout<<"\n";
    dfs3(root);cout<<"\n";
	return 0;
}

这道题，我的想法是找到根节点，做三次dfs。

先序，中序，后序都是按照根与左右子树的顺序进行区分。

比如中序遍历：当没有节点左子树，此时应当输出根，再去遍历右子树。

---

接下来说一说二叉树的性质

二叉树中有两种特别的树：满二叉树，完全二叉树

满二叉树：

一棵深度为k且有2k–1个结点的二叉树,称为满二叉树。

通常来说我们对满二叉树的结点进行连续编号，约定从根结点起，自上而下，从左到右进行编号

完全二叉树：

深度为k，有n个结点的二叉树

仅当其每一个结点都与深度为k的满二叉树中编号从1到n的结点一一对应时，称为完全二叉树。

特点：k-1层以前是满二叉树，最后 一层节点从左到右连续出现

---

这一章我只挑重点的来讲qwq

小球和FBI都是找规律,并没有太大的意义（事实上是我懒得从打一遍）

---

例12.5-2 二叉树遍历转化

描述

一棵二叉树有不超26个节点，每个几点用大写字母表示，现在给定树的中序遍历和先序遍历结果，请输出该树的后序遍历结果。

输入描述

第一行： 树的中序遍历结果
第二行： 树的前序遍历结果

输出描述

单独的一行表示该树的后序遍历。

#include
using namespace std;
string z,q;
#pragma once
#pragma GCC diagnostic error "-std=c++11"
#pragma GCC target("avx")
#pragma GCC optimize(2)
#pragma GCC optimize(3, "Ofast", "inline")
#pragma GCC optimize("Ofast")
#pragma GCC optimize("inline")
#pragma GCC optimize("-fgcse")
#pragma GCC optimize("-fgcse-lm")
#pragma GCC optimize("-fipa-sra")
#pragma GCC optimize("-ftree-pre")
#pragma GCC optimize("-ftree-vrp")
#pragma GCC optimize("-fpeephole2")
#pragma GCC optimize("-ffast-math")
#pragma GCC optimize("-fsched-spec")
#pragma GCC optimize("unroll-loops")
#pragma GCC optimize("-falign-jumps")
#pragma GCC optimize("-falign-loops")
inline void dfs(int x,int l,int r){
    if(l>r) return;
    int tot=z.find(q[x]);
    dfs(x+1,l,tot-1);
    dfs(x+tot+1-l,tot+1,r);
    printf("%c",z[tot]);
}
int main(){
	cin>>z>>q;
   dfs(0,0,z.size()-1);
	return 0;
}

为什么我能求出来呢？

一颗二叉树如果知道中序遍历，以及先序(或后序)，我们就能清晰的知道树的结构。

所以在打CSP的时候,经常出这种题~

直接懒得画了图了~

---

例12.5-4 二叉树点值修改

描述

有一颗n(n<=1e5)个点的二叉树，初始点权为0。保证根节点为1，现在进行m次(m<=2e5)修改。
每次修改均给定x,k（k={1，2，3}）两个数。

k=1：表示将节点以及左子树中每一个左儿子的点值都加上1；
k=2：表示将节点以及右子树中每一个右儿子的点值都加上1；
k=3：表示将节点以及左右子树中所有的儿子都加上1。

请问：经过修改后这棵树的所有点值和是多少？

输入描述

第一行两个整数n,m
接下来n行每行三个整数a,b,c表示节点a的左儿子b和右儿子c。
随后m行表示若干次修改。

输出描述

一个整数

#include
using namespace std;
const int N =1e5+5;
#pragma GCC optimize(3)
#pragma GCC optimize(2)
#pragma GCC optimize(1)
#pragma GCC optimize("inline")
#pragma GCC optimize("Ofast")
int rs[N],ls[N],fa[N];
int n,m;
long long tr[N],tl[N],t[N],ans;
inline void f (int x){
    if(x==0) return;
    ans+=tr[x]+tl[x]+t[x];
    tl[ls[x]]+=tl[x],t[ls[x]]+=t[x];
    tr[rs[x]]+=tr[x],t[rs[x]]+=t[x];
}
inline void dfs1(int x){
    if(0==x) return;
    f(x);
    dfs1(ls[x]);
    dfs1(rs[x]);
}
int main(){
    scanf("%d %d",&n,&m);
    for(register int i=1;i<=n;i++){
        int x,y,z;
        scanf("%d %d %d",&x,&y,&z);
        ls[x]=y,rs[x]=z;
        fa[y]=fa[z]=x;
        ;
    }
    for(register int i=0;i<m;i++){
        int x,y;
        scanf("%d %d",&x,&y);
        if(x==2) tr[y]++;
        if(x==1) tl[y]++;
        if(x==3) t[y]++; 
    }
    dfs1(1);
    printf("%lld",ans);
}

敲黑板!!!

这道题引入了一个新的知识点

‘懒标记’

懒标记也叫延迟标记，顾名思义，我们再修改这个区间的时候给这个区间打上一个标记，这样就可以做到区间修改的的O(nlogn)时间复杂度。

我在每一次DFS时才会更新一次,大大的节省了时间

---

六.图的概念及储存遍历

图（Graph）是由若干给定的顶点及连接两顶点的边所构成的图形，通常表示为G={V,E}。

其中，G表示一个图，V是图G中顶点的非空集合，E是图G中边的集合。我们前面说过的树则是一张特殊的图

这是一幅图：

//图与树的区别：
//树中任意两点只有一条路径连通，而图没有这个限制。这个区别使得节点不再具备父子关系，图中也可能存在环。
//所以无根有环，使得图没有树中层次关系，多用来表示某些事物的网络关系，在现实生活中，十分常见。

图的常见分类

1.无向图：图的边没有方向，可以双向。

2.有向图：图的边有方向，只能按箭头方向从一点到另一点。稠密图：一个边数接近完全图的图。

3.稀疏图：一个边数远远少于完全图的图。

4.完全图：一个n 阶的完全无向图含有n*(n-1)/2 条边；一个n 阶的完全有向图含有n*(n-1)条边；

5.竞赛图：一个n 阶的竞赛图的意思去掉方向后是一个无向完全图。(不便展示)

制作不易 点个赞再走吧