BFS与DFS初级练习(排列数字，n-皇后，走迷宫)

BFS与DFS初步了解

DFS（深度优先搜索）和BFS（广度优先搜索）是两种常用的图遍历算法。

DFS是一种递归的搜索算法，它从起始节点开始，沿着路径依次访问与当前节点相邻的未访问节点，直到无法继续访问时回溯到上一个节点，并选择另一个未访问节点进行访问，直到所有节点都被访问完毕或者找到目标节点。DFS的特点是先深度后广度，即优先探索深度方向的节点。

BFS是一种迭代的搜索算法，它从起始节点开始，依次访问与当前节点相邻的未访问节点，并将这些节点按照访问的顺序加入一个队列中，然后再按照队列中节点的顺序依次访问队列中的节点，直到队列为空或者找到目标节点。BFS的特点是先广度后深度，即优先探索广度方向的节点。

这两种算法的实际中运用十分多，在竞赛中很多题也能用搜索解决，所以对DFS,BFS的掌握就十分重要。下面是一些dfs,bfs经典但是难度又不高的例题

BFS

排列数字​​​​​​

给定一个整数 n，将数字 1∼n排成一排，将会有很多种排列方法。

现在，请你按照字典序将所有的排列方法输出。

输入格式

共一行，包含一个整数 n。

输出格式

按字典序输出所有排列方案，每个方案占一行。

数据范围

1≤n≤7

输入样例：

3

输出样例：

1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1

DFS关键在于递归结束条件的选择，状态标记，递归后的恢复。

像这道题就可以使用深搜解决

我们可以构造如图的一颗树，每次选择一个数都是往下，如果往下没有路了，则回溯到上一步，经典的DFS操作。

想要实现上图的操作，我们需要一个st数组，用于记录每个点是否被访问过，辅助搜索。

此题中还需要递归后恢复标记，不然回溯之后没有未被访问的点可以使用。

#include
using namespace std;
const int N = 10;
int n;
//用于记录路径
int path[N];
//记录某个点是否使用过 用于辅助dfs操作
bool st[N];

void dfs(int u)
{
    //如果到了末尾 第N层 则是一个答案 return
    if(u == n) 
    {
        for(int i = 0;i>n;
    dfs(0);
    return 0;
}

n-皇后问题

n−皇后问题是指将 n 个皇后放在 n×n的国际象棋棋盘上，使得皇后不能相互攻击到，即任意两个皇后都不能处于同一行、同一列或同一斜线上。

现在给定整数 n，请你输出所有的满足条件的棋子摆法。

输入格式

共一行，包含整数 n。

输出格式

每个解决方案占 n行，每行输出一个长度为 n的字符串，用来表示完整的棋盘状态。

其中 . 表示某一个位置的方格状态为空，Q 表示某一个位置的方格上摆着皇后。

每个方案输出完成后，输出一个空行。

注意：行末不能有多余空格。

输出方案的顺序任意，只要不重复且没有遗漏即可。

数据范围

1≤n≤9

输入样例：

4

输出样例：

.Q..
...Q
Q...
..Q.

..Q.
Q...
...Q
.Q..

n皇后是非常经典的一道DFS题，学会这道题对DFS的理解会更加透彻。

首先理解什么是n皇后问题，即在一个nxn的棋盘上放置皇后，其中任意两个皇后都不能在同一行，同一列，同一正对角线，同一负对角线上。

棋盘是个矩阵，我们一行一行的继续计算，还是核心思想：递归结束条件的选择，状态标记，递归后的恢复。

状态标记:

因为我们是一行一行进行计算，每行我们只放一个，所以行的状态我们不用进行标记。所以我们需要三个数组进行标记状态：

行，列，对角线我们都从 0 ~n进行编号

col[N]   用于标记某列上是否有皇后 有为1 没有为0

dg[N]    用于标记某正对角线上是否有皇后 有为1 没有为0

udg[N]  用于标记某负对角线上是否有皇后 有为1 没有为0

对列的标记十分简单，但是对角线的标记不是很好理解，下面利用画图辅助理解

我们将棋盘放到坐标系，以正对角线为例，用图中的画法，我们可以发现，每条对角线的编号正好是直线在y轴上的截距，直线方程为: y = -x + b

我们需要的是b，所以 b = y + x   这样我们就得到了正对角线的编号方程,代码中y轴对应行u，x轴对应 y轴 i ,所以正对角线的编号方程为 u+i

同理可以得到副对角线方程 u-i,因为是相减，可能会有负数出现，所以加上偏移量n，防止负数出现

准备工作已经完成，接下来是DFS的思路

递归结束条件的选择：

要求col[N]，dg[N]，udg[N]三个数组同时为0，即都没有使用过时，放置皇后。  

递归后的恢复:

递归结束后要恢复状态，以便下一次递归

​
#include
using namespace std;
const int N = 20;
//dg[N]记录正对角线上元素是否被使用过 udg记录负对角线上元素是否被使用过 col记录列
int dg[N],col[N],udg[N];
//记录操作
char path[N][N];
int n;

void dfs(int u)
{
    //u表示行 到最后一行输出
    if(u == n)
    {
        //输出
        for(int i = 0;i>n;
    //初始化为.
    for(int i = 0;i

BFS

 迷宫问题

给定一个 n×m的二维整数数组，用来表示一个迷宫，数组中只包含 0 或 1，其中 0 表示可以走的路，11表示不可通过的墙壁。

最初，有一个人位于左上角 (1,1)处，已知该人每次可以向上、下、左、右任意一个方向移动一个位置。

请问，该人从左上角移动至右下角 (n,m) 处，至少需要移动多少次。

数据保证 (1,1)处和 (n,m) 处的数字为 0，且一定至少存在一条通路。

输入格式

第一行包含两个整数 n 和 m。

接下来 n 行，每行包含 m个整数（0 或 1），表示完整的二维数组迷宫。

输出格式

输出一个整数，表示从左上角移动至右下角的最少移动次数。

数据范围

1≤n,m≤100

输入样例：

5 5
0 1 0 0 0
0 1 0 1 0
0 0 0 0 0
0 1 1 1 0
0 0 0 1 0

输出样例：

8

迷宫问题也是一种最短路问题，解决方法很多，这里我们利用BFS解决。

BFS因为是一层一层搜索，所以到图中权值都为1时，每第一次搜到这个点，一定是最短路径

BFS通常使用队列辅助计算

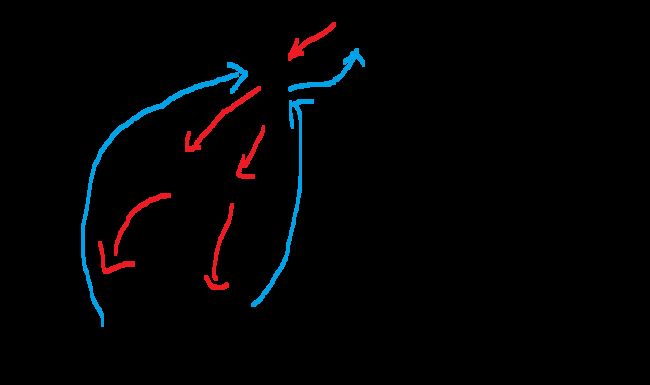
如图是BFS的思路 也是模板，我们可以将迷宫看成图，从左上角开始移动，可以上下左右移动，所以我们可以将这点的上下左右看成一层，我们一直枚举一层中的所有元素，如果符合条件，就入队，往下一层枚举。 总的来说 BFS难度要比DFS低，也更加容易理解

图中数字表示层数

题解中利用了STL中的queue与pair,如果stl不熟练可以自行上网搜索

代码中注释写的十分详细，所以也不过多赘述。

#include
#include
#include
using namespace std;
const int N = 110;
int n,m;

//用于存储地图 0可以通过 -1表示路障
int g[N][N];
//用于存储每个点的距离 为-1表示没到过这个点
int d[N][N];
typedef pair PII;
queue q;
//记录下这个点是从哪个点走过来的，保存路径
PII Prev[N][N];

int bfs()
{
    //从左上角0,0开始走
    q.push({0,0}); 
    //刚开始每个点的距离要初始化为-1 因为每个点都没到过
    memset(d,-1,sizeof d);
    //从左上角0开始走
    d[0][0] = 0;
    //用dx dy数组表示在地图中往上下左右走的坐标变化
    int dx[4] = {1,0,-1,0},dy[4] = {0,1,0,-1};
    //队列不为空
    while(!q.empty())
    {
        //从队列中弹出队头 t
        auto t = q.front();
        q.pop();
        //表示往上下左右走四个方向试探
        for(int i = 0;i<4;i++)
        {
            //通过四次循环列出四个方向走的坐标，后面再进行判断 这样可以剩下4个判断
            int x = dx[i]+t.first,y = dy[i]+t.second;
            //x,y坐标要在图内,图上为0才能走(-1表示路障),d[x][y]要为-1(表示未到过这个点)
            if(x >= 0 && x=0 && y>n>>m;
    for(int i = 0;i>g[i][j];
        }
    }
    
    cout<

此篇为新手学习总结用，为了加深记忆，所以有错误可以指出，谢谢大家观看