算法day11

算法day11

• 239 滑动窗口最大值
• 237 前K个高频元素
• 栈与队列总结

---

滑动窗口最大值

第一想法，暴力解：这个解法会超时。（这就是为啥是困难题）
思路：每到一个新的窗口，就重新进行一次窗口中的max迭代，迭代完成后把max的值加入，结果集中，注意每次迭代完之后都需要重置max的值，因为不重置可能会保留上一个窗口的结果。

import "math"
func maxSlidingWindow(nums []int, k int) []int {
    
    res:=[]int{}
    
    for i:=0;i<=len(nums)-k;i++{
        var max int = math.MinInt32
        for j:=i;j<i+k;j++{
            if nums[j]>max{
                max = nums[j]
            }
        }
        res = append(res,max)
    }

    return res
}

解题解法（最优解）：单调队列，而且这个队列还是个双端队列
我当时看讲解，逻辑搞懂了，代码突然给我来个从队尾删除元素给我整傻了。这里非常要注意。它用了但是题解没说，我真无语了。

对于做这个题来说，如果要用队列来做，那我们想要一个怎样的队列：
那你可以想想这个场景，往后滑动的过程中，实际上是元素出队列，和元素进队列，然后获取一次队列中最大值的过程。
通过对这个场景的思考，那显然这个队列有这三个功能：
1.pop：如果移除的元素value等于单调队列的出口元素，那么队列弹出元素，否则不用任何操作
注意这个说法是在遍历这个数组这种情形下来说的。
2.push：如果push的元素value大于入口元素的数值，那么就将队列入口的值弹出，直到push元素的值小于等于队列入口元素的数值为止。
3.getMaxValue：得到队列中的最大值（而且得到队列中最大值的操作的时间复杂度是o(1)，如果是o(n)量级那就和暴力解没太大区别了）

那这个队列的功能需要我们自己去实现，这里就可以引出啥叫单调队列了，满足上面这三个功能的队列就叫单调队列。由于我们的操作导致，我们维护的这个队列会具有单调性，所以被称为单调队列。

这个队列应该长这个样子：

class MyQueue {
public:
void pop(int value) {
}
void push(int value) {
}
int front() {
return que.front();
}
};

其实我个人认为这个描述，本身上没啥问题，但是你就是看不懂，甚至写不出代码。

经过思考我这里再做一个解读和举个例子
我发现一件事，这个滑动窗口和我们维护的队列千万别混为一回事，你模拟归模拟，但是实际的操作会很不一样。
通过模拟的过程，我会一直进行遍历nums，然后从滑动窗口中找最大值，如果我们把这个模拟的过程当成入队和出队的过程，那对于这个滑动窗口来说显然是这么回事。
但对于维护的单调队列而言，我的pop操作的执行是有条件的，不是像下面模拟的滑动窗口一样无脑出队入队。

例子：

单调队列的队头就是这个滑动窗口区间的最大值。 这个是核心

看了很多题解我觉得这个例子拿来讲这个单调队列的维护操作是最好的。由于我们维护的是单调队列，刚开始队列为空，那么2先入队，然后1比2小入队没问题，然后4进行入队。此时2和1这两个元素要进行出队，因为在后续的过程中，2和1是不可能超过这个1的，所以队列中维护2和1将没有意义，此时队列中只有一个4.
然后2进行入队，3入队后这个2将出队，因为只要有3在，在后续的过程中2就不可能成为最大值。此时的模拟区间是4，2，3.但我维护的单调队列的内部是4，3。
然后窗口再后移，4就要进行出队了，4往后滑动就不在我模拟的这个窗口中了，此时把4pop出队列的条件就是当队头元素等于我们滑动的这个模拟窗口的最前面的元素。
4pop出去后，我现在模拟区间窗口到了2 3 2，此时队列中只有一个3.

上面的例子是讲如何维护我们的队列的。
现在我认为看完这个过程可以直到push和pop为啥要这么设计了。
我甚至可以根据这个逻辑直接写出push和pop的代码
push(val int) : 插入的这个元素就是区间往后之后新加入区间的那个元素， 插入这个元素，要将这个元素从队列的尾部依次进行比较删除操作，当一旦元素比插入的这个小队尾的这个元素要大，那么队尾的这个元素就必须要删除，（这个为什么我解释过了，就是上面说的，后面这个元素进来，前面比它小的元素就没有当老大的机会了。）直到找不到比它小的元素删除，那就把这个元素插入到队尾。

pop(val int)：仍然是针对队列的，参数是区间最前面的元素，这个元素要与队列的队头进行相等判断，如果相等，那么pop掉这个队头元素，如果不相等 ，pop啥也没干。为什么要这么做，这么做的原因是我也在上面的过程中说了，区间423 向232 转化的时候，4已经要划出去了，而窗口是和队列是对应的，那么队头肯定要把这个元素干掉。

那代码该怎么写：这里还是要做解读，因为我当时还是搞混了，看到题解代码还是一脸懵。

代码思维讲解：
用个例子来说明这个过程：

每次窗口移动的时候，调用que.pop(滑动窗口中移除元素的数值)，que.push(滑动窗口添加元素的数值)，然后que.front()就返回我们要的最大值。 这是代码的整体逻辑。

现在我来完整的用代码逻辑来讲一遍：
1.初始状态，滑动窗口在1 3 -1，队列为空
2.先处理前k个，这个过程我称之为讲窗口与队列先完成初步匹配，这个对于代码来说就是先进行三个push操作。因为窗口一开始已经有了。
3.由于队列本身为空，1先加入队列，然后3加入时，由于3比1大，所以1没必要存直接出队，然后-1再入队，由于-1比3小，满足单调队列的单调性。此时队列的状态是3 -1。这个步骤3做完了，这个队列就和滑动窗口的初始状态匹配上了。由于队头元素就是区间最大值，此时就把队头元素加入结果集。
4.现在窗口就要开始滑动了，对于我的窗口来说，一直要滑动到这个序列的末尾，在这个过程中每滑动一次窗口就一次调用que.pop(滑动窗口中移除元素的数值)，que.push(滑动窗口添加元素的数值)，然后que.front()就返回我们要的最大值，然后把这个值加入结果集。这么做的原因就是我必须伴随滑动窗口的变化更新这个维护单调队列。
5.注意我的pop操作和push操作的实现逻辑上是针对队列的，但是再整体代码逻辑上又像是对滑动窗口这个类似像队列一样的东西在搞pop和push。
6.对于队列的pop和push的逻辑我在上面已经说明了。就是这样的逻辑。
7.这样的过程一直伴随着滑动到末尾的过程中一直处理就完事了。

现在我感觉我无敌了代码那可以说是随便写：
整体逻辑：
1.先把这个队列实现了，它的相关操作也实现了
2.main函数就是先三个入队，存依次结果集，然后后面的窗口每滑动一次，就更新一次pop的状态：pop一次和map一次，然后取队头元素加入结果集。
3.返回结果集

type MyQueue struct {
    queue []int
}

func NewMyQueue() *MyQueue {
    return &MyQueue{
        queue: make([]int, 0),
    }
}

func (m *MyQueue) Front() int {
    return m.queue[0]
}

func (m *MyQueue) Back() int {
    return m.queue[len(m.queue)-1]
}

func (m *MyQueue) Empty() bool {
    return len(m.queue) == 0
}

func (m *MyQueue) Push(val int) {
    for !m.Empty() && val > m.Back() {
        m.queue = m.queue[:len(m.queue)-1]
    }
    m.queue = append(m.queue, val)
}

func (m *MyQueue) Pop(val int) {
    if !m.Empty() && val == m.Front() {
        m.queue = m.queue[1:]
    }
}

func maxSlidingWindow(nums []int, k int) []int {
    queue := NewMyQueue()
    length := len(nums)
    res := make([]int, 0)
   
    for i := 0; i < k; i++ {
        queue.Push(nums[i])
    }
    
    res = append(res, queue.Front())

    for i := k; i < length; i++ {
        queue.Pop(nums[i-k])
        queue.Push(nums[i])
        res = append(res, queue.Front())
    }
    return res
}

思考的难点：
1.把区间移动的过程和维护队列理解成一回事，把自己整懵了。
2.看代码的时候我看到有一个从队列的尾部删除元素的操作，我当时寻思我的队列怎么能从队尾删除元素，我这里相当于束缚了自己的思想，因为我太纠结于定义，如果我是个双端队列呢，这个队列是我自己定义和实现的，所以想它是双端，它就可以是双端。

---

前K个高频元素

我拿到这个题的第一想法，是用排序来做，但是注意这个排序不是对数组进行排序。
思路：用map[]，key存元素，value存该元素的计数值。然后我就想要是能将map根据count值进行个排序，然后我直接遍历map，结果切片res直接append键值就做完了。
基于这个思路的实现：

func topKFrequent(nums []int, k int) []int {
    if len(nums)==1{
        return nums
    }

    m1:=make(map[int]int)

    for i:=0;i<len(nums);i++{
        m1[nums[i]]++
    }

    type kv struct{
        key int
        value int
    }

    var ss []kv
    for k,v := range m1{
        ss=append(ss,kv{k,v})
    }

    sort.Slice(ss,func(i,j int )bool{
        return ss[i].value>ss[j].value
    })

    res := []int{}

    for _,v := range ss {
        k--
        res=append(res,v.key)
        if k==0{
            return res
        }
    }

    return res

    
}

我在写这个写法的时候遇到的问题：
1.map怎样才能进行排序？
map想要实现在map的基础上进行排序是不可能的，这里想实现排序就只能将map转结构体切片。实现方法：先创建一个结构体类型，然后再创建一个结构体切片。然后遍历这个map。然后对这个结构体切片进行append。
这个结构体的结构和我的map必须一样，因为后续将用来做转化

 type kv struct{
        key int
        value int
    }

var ss []kv 创建一个结构体切片，用于存map转化后的结构

for k,v := range m1{
        ss=append(ss,kv{k,v}) 
    }

因为ss是结构体切片，而kv是结构体实例，所以我现在就相当于在append该类型的元素。
{k,v}就是直接进行实例化然后添加了。

2.怎么排序，sort.slice 是非常强大的，所以可以使用sort.slice对结构体的字段进行排序。这里排完序之后就是按计数值从大到小排序，所以这里直接遍历这个结构体，添加它的key就可以了。

总结：
我个人认为我这个思路是可以的，但是写法不太好，太依赖库函数。

这里我再写一个道理相同的另一种实现方式

func topKFrequent(nums []int, k int) []int {
    ans:=[]int{} //创建一个空切片
    map_num:=map[int]int{} //创建一个空map
    for _,item:=range nums { //先统计每种数字的频数
        map_num[item]++
    }
    for key,_:=range map_num{ //遍历这个map，把数的种类都插入ans切片中
        ans=append(ans,key)
    }
    //核心思想：排序
    //可以不用包函数，自己实现快排
    sort.Slice(ans,func (a,b int)bool{ 
        return map_num[ans[a]]>map_num[ans[b]]
    })
    return ans[:k] //排序好了取前k个。
}

这种写法我主要是语法不太会，居然还有这样的操作，这里进行学习。

for key,_:=range map_num{ //遍历这个map，把数的种类都插入ans切片中
        ans=append(ans,key)
    }

把遍历map，把数字种类（key）先装入切片中。
然后对这个切片进行排序，排序的判断函数是依据map_num[ans[a]]>map_num[ans[b]],这个的意思是依据元素在map_num[]中的value值进行排序的。a，b是下标，ans就是切片。
这个要求对这个排序函数也要有一定的熟练度

题解版本：

题解的解法是用到了堆来做：这里先进行堆的学习：
堆的定义：
堆必须是个完全二叉树，就是这种按序排的，而且中间不能跳

堆序性：根据堆序性可以把堆分为两类
也就是这个堆中的每个结点都保证这样的性质（递归定义）
举例：

可以看到每个结点就满足根结点大于左右子节点（而且是递归的满足）
可以看出根结点小于子结点，而且递归满足。

堆的存储
这完全就是按照完全二叉树来存储

堆的基本操作：向上调整和向下调整
这个我个人觉得要理解：因为是对不同的场景
向下调整
场景：在一个大根堆中，某元素不满足堆序性，比如这个1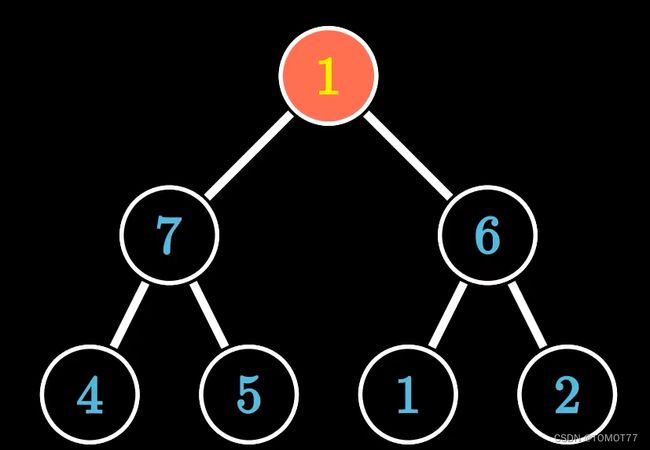
那我就需要按照大根堆的定义来进行调整，显然大的要网上走，小的就往下面去。
这里的交换原则是，下一层进行比较，比如7，和6进行比较，然后7更大，1与更大的7进行交换，这样的操作一直往下递归的进行。直到满足大根堆的性质为止：

此时可以发现，这种把结点1不断向下调整的操作就叫向下调整。显然向下调整的时间复杂度为o(logn)，这就是树高。

向上调整：
在大根堆中这个8显然要放到堆顶去，那这样以大根堆的定义为基准进行调整，6和8进行交换，然后7和8进行调整。直到所有元素满足堆序性。

这种向上面不断走的调整，就称之为向上调整。
这个应用场景一般都是用在插入新元素到堆中。复杂度显然也是logn

建堆
有两种方法，自顶向下和自下向上。
自顶向下就是一开始啥也没有，然后不断往堆中插入元素，一边插入一边进行**向上调整。显然nlogn的复杂度。
自下而上：
所有直接对这个数组进行操作，把这个数组的结构就理解成堆，然后从最后一个非叶子结点开始以性质为基准进行向下调整。**有时候往下调整一层还不够，那就再往下调整下层即可。这种建堆的复杂度是o(N)

堆的具体应用：
优先队列：
优先队列是一种数据结构，它允许在任何时候都可以高效的访问队列中到的最高（或最低）优先级的元素。它不是指的具体的堆类型，而是可以通过不同的底层数据结构实现，其中堆（特别是二叉堆）是实现优先队列的一种常用方式。

堆与优先队列：
小根堆（最小堆）： 在小根堆中，父节点的值总是小于或等于其子节点的值。因此，堆顶（根节点）是整个堆中的最小值。小根堆可以实现最小优先队列。
大根堆（最大堆）： 在大根堆中，父节点的值总是大于或等于其子节点的值。因此，堆顶是整个堆中的最大值。大根堆可以实现最大优先队列。

优先队列的操作：
入（Push）： 将一个新元素添加到优先队列中。在堆实现中，这通常涉及将元素添加到堆的末尾，然后执行上浮操作以保持堆的性质。
弹出（Pop）： 移除并返回优先队列中优先级最高（或最低）的元素。在堆实现中，这通常涉及移除根节点，将堆的最后一个元素移动到根位置，然后执行下沉操作以保持堆的性质。
查看顶部（Peek/Top）： 返回但不移除优先队列中优先级最高（或最低）的元素。
大小（Size）/是否为空（IsEmpty）： 返回优先队列中的元素数量或检查队列是否为空。

由于每次弹出都会弹出一个最大元素，或者最小元素，那么这个性质就是堆排序的思路。

正式来看这个题

其实没必要对所有元素进行排序，我们求的是前k个高频元素，我们只需要维护k个有序集合就可以了，没有必要对所有元素都进行一个排序。如何去维护k个高频元素的一个有序的一个集合？
就要用到堆这种数据结构体：
这个数据结构非常的适合用来求前k大和前k小这样的操作。
那这种数据结构如何实现求前k大，其实只需要用堆去遍历一遍这个map里面的所有元素，然后堆里面就维持个元素。然后堆里面存key值。遍历完之后这个堆里面的所有元素就是前k大。

这就有个问题，用的是大顶堆还是小顶堆。回答是用小顶堆，虽然大顶堆非常的符合我们预期的感觉，但是从大顶堆的操作来说，这种结果其实实现不出来。
因为堆里面限定元素个数为k个，当我遍历的时候就意味着，我遍历一个新元素的时候，就是对这个元素添加进堆，这个操作一般是放在堆尾部，由于要维持元素个数为k，那就要pop一个元素，而大顶堆的pop元素是从堆顶弹出的，这个就是大顶堆的要求。那这个过程显然得不到我们想要的答案。因为大的元素显然会被弹出。 这样你就会发现一件事，因为我们总是把大的弹出，所以对于大顶堆来说，最后得到的这个结果其实是前k小。
这个过程的理解需要对堆足够熟悉。

所以 做这个题就需要用小顶堆。推导过程和上面一样。注意以value为基准进行插入，然后输出对应的key

这个代码我是看了题解才写出来的。

代码思路：
1.先创建map[int]int,这个map是用于统计频数的。应该是遍历map来建堆而不是去直接遍历切片。
2.这个小顶堆要自己来实现
3.遍历map的时候，元素插入，然后调整，一直迭代完map，最后堆中的元素就是前k大。

func topKFrequent(nums []int, k int) []int {
    map_num:=map[int]int{}
    //记录每个元素出现的次数
    for _,item:=range nums{
        map_num[item]++
    }
    h:=&IHeap{}
    heap.Init(h)
    //所有元素入堆，堆的长度为k
    for key,value:=range map_num{
        heap.Push(h,[2]int{key,value})
        if h.Len()>k{
            heap.Pop(h)
        }
    }
    res:=make([]int,k)
    //按顺序返回堆中的元素
    for i:=0;i<k;i++{
        res[k-i-1]=heap.Pop(h).([2]int)[0]
    }
    return res
}

//构建小顶堆
type IHeap [][2]int

func (h IHeap) Len()int {
    return len(h)
}

func (h IHeap) Less (i,j int) bool {
    return h[i][1]<h[j][1]
}

func (h IHeap) Swap(i,j int) {
    h[i],h[j]=h[j],h[i]
}

func (h *IHeap) Push(x interface{}){
    *h=append(*h,x.([2]int))
}
func (h *IHeap) Pop() interface{}{
    old:=*h
    n:=len(old)
    x:=old[n-1]
    *h=old[0:n-1]
    return x
}

解读：
1.type IHeap [][2]int，这个建堆是怎么个事？为什么要用二维数组？而且里面还是个[2]int。
这里的解释是里面这个[2]int同时存储了两类重要信息：元素的值和该元素的频率。[0]存数值，[1]存频率。这种处理我觉得非常有必要学习，反正我不会。
这种处理有啥好处？非常的适合用于比较,比如调整的过程就是比较value值的过程，就相当于比较的int[1]，获取元素就是int[0]。当我们向堆中添加元素时，我们实际上添加的是[2]int{数值，频率}。

2.func (h IHeap) Len()int {
return len(h)
}
这个还是很简单的，有了1.的理解，h的内部是一个一个的切片，每个切片代表一个k-v，所以这里直接从切片的数量就直接判断了元素的个数。
3.func (h IHeap) Less (i,j int) bool {
return h[i][1] }
这个单纯的就是个比较函数，用于比较不同数的频数。

4.func (h IHeap) Swap(i,j int) {
h[i],h[j]=h[j],h[i]
}
交换操作，这里就是换切片位置就行了。

5.func (h *IHeap) Push(x }) {
*h=append(*h,x.([2]int))
}

插入操作，注意这里是指针，因为会修改堆的结构。
x是任意类型，x.([2]int)这个操作是类型断言，这里有个语法知识
如果x是空接口类型，那么如果你想对他进行操作，它必须要转换成具体类型才可以进行使用。所以就要进行类型断言。
*h=append(h,x.([2]int))这个代码要搞个p这是为了解引用，因为接收者那里传的是指针类型。
然后将x这个[2]int切片插入到h这个切片数组的末尾。

6.func (h *IHeap) Pop() interface{}{
old:=*h
n:=len(old)
x:=old[n-1]
*h=old[0:n-1]
return x
}
这个是切片的弹出操作，返回值是任意类型
之前也介绍过堆的弹出操作的具体流程。
old 先等于堆的引用类型，也就是现在old是[2]int类型的切片。
n计算切片的长度，也就是计算里面的元素个数。
x等于切片的末尾元素。
此时再更新堆，并返回刚刚删除的那个元素x。

这里我做一个总结，我当时看这个代码云里雾里，那是因为它隐藏了go语言很多的语法知识以及库函数的使用。

我当时看完这几个函数，我以为直接就是针对这个堆的操作了，但我看了代码逻辑之后发现，并不是。但是我提交的适合发现结果过了。而且我发现这些函数在main函数里面没体现出来，我甚至怀疑这些函数有意义吗？都没用为啥要定义。

这里我做一个解读：
从main函数里我发现了端倪：
我发现关键的操作居然是heap.Init(h)这样对heap这个不知道哪里来的东西进行操作。
这里我才知道调了库函数。一开始我以为是手搓堆，原来还是调包。这里我就对heap进行解读。
heap是container/heap的一部分，这个包提供了堆操作的接口和函数，允许用户实现任何满足 heap.Interface 的类型的堆操作。它主要用于实现优先队列结构。

heap.Interface 是一个接口，要求实现以下方法：

Len() int: 返回堆中的元素数量。
Less(i, j int) bool: 报告索引 i 的元素是否应该排在索引 j 的元素之前。
Swap(i, j int): 交换索引 i 和 j 的元素。
要使用 container/heap 包的功能，您需要定义一个类型（比如 IHeap），并为这个类型实现上述方法。

heap 包的功能
container/heap 包提供了几个重要的函数，用于操作满足 heap.Interface 的任何类型：

Init(h Interface): 对初始堆 h 进行排列，以满足堆属性。
Push(h Interface, x interface{}): 向堆 h 中添加元素 x。
Pop(h Interface) interface{}: 从堆 h 中弹出并返回顶部元素。

使用方式
定义堆类型： 首先，定义一个自定义类型（如 IHeap），并为这个类型实现 heap.Interface 的方法。
初始化堆： 使用 heap.Init 初始化您的堆，确保它满足堆属性。
添加和移除元素： 使用 heap.Push 和 heap.Pop 向堆中添加元素和从堆中移除元素。这些操作会自动维护堆的性质。

示例

type IHeap []int  // 自定义类型

func (h IHeap) Len() int { ... }
func (h IHeap) Less(i, j int) bool { ... }
func (h IHeap) Swap(i, j int) { ... }
func (h *IHeap) Push(x interface{}) { ... }
func (h *IHeap) Pop() interface{} { ... }

func main() {
    h := &IHeap{...}
    heap.Init(h)
    heap.Push(h, value)
    top := heap.Pop(h)
}

经过这些了解我已经看得懂主函数了。

func topKFrequent(nums []int, k int) []int {
    map_num:=map[int]int{}
    //记录每个元素出现的次数
    for _,item:=range nums{
        map_num[item]++
    }
    h:=&IHeap{}  /创建一个堆
    heap.Init(h)  //初始化堆
    //所有元素入堆，堆的长度为k
    for key,value:=range map_num{//遍历map
        heap.Push(h,[2]int{key,value}) //先进行插入堆操作
        if h.Len()>k{ //一旦我插入的超过了k，那么就要进行弹出操作
            heap.Pop(h)
        }
    }
    res:=make([]int,k)
    //按顺序返回堆中的元素
    for i:=0;i<k;i++{
        res[k-i-1]=heap.Pop(h).([2]int)[0]  //这里要倒着来，因为先弹出的是堆顶，堆顶是最小所以放后面
    }
    return res
}

接下来可以回答上面提出的问题了，我还定义了一堆heap接口的函数有啥用，这个函数是为heap.Init, heap.Push 和 heap.Pop这三个函数服务的，它的内部会进行调用。
我举个例子
我当时以为pop我下面实现的pop会对应着堆的弹出堆顶的操作，结果我看了代码不是，后面我找到了答案：
当我调用heap.Pop(h)时实际上首先调用我的Pop方法来切除切片的最后一个元素，然后执行下沉操作。

我的问题又来了：既然我要完成这个代码的编写，前面我已经知道Pop方法是接口定义的方法，但是我想不到为什么Pop要这么设计。为什么Pop操作设计成删除切片最后一个元素。
回答：首先我在学数据结构的适合就知道，删除堆顶元素，那么就要用最后一个元素替换堆顶元素，这是为了保持完全二叉树的性质。所以这里对换之后删除的最后一个元素，实则是堆顶元素。

看懂了之后我就该总结怎样才能把这个代码写出来了：
要理清逻辑：
分为四大块：
1.先map统计频数
2.构建小顶堆
3.将元素和频率放入堆中，就是单纯的heap.push如果超了k就heap.pop
4.提取结果，就是不断地弹出堆顶元素倒序放入结果集就可以了
5.自定义堆必须要实现heap结构地方法

type IHeap [][2]int

func (h IHeap) Len() int { ... }
func (h IHeap) Less(i, j int) bool { ... }
func (h IHeap) Swap(i, j int) { ... }
func (h *IHeap) Push(x interface{}) { ... }
func (h *IHeap) Pop() interface{} { ... }

这些代码可以不用背：因为已经规定了这些方法地作用，所以只用根据作用来实现这些必须实现地方法就可以了。
Len() 方法用于返回堆中的元素数量。
Less(i, j int) bool 方法定义了堆中元素的排序准则。对于最小堆，它应该报告索引 i 的元素是否小于索引 j 的元素；对于最大堆，则相反。
Swap(i, j int) 方法交换堆中的两个元素。
Push(x interface{}) 方法向堆中添加一个新元素（插在尾）。
Pop() interface{} 方法从堆中移除并返回顶部元素。
这个Pop要注意一点，这里是逻辑上从堆中删除堆顶元素，但是物理上（也就是对底层的末尾元素的删除）。因为这个过程实际上是堆顶和堆尾做对换，然后删除堆尾比较容易。

写的时候的问题：
1.这个堆我真写不来。所以复习的时候，这个堆的实现一定要过关。里面有的语法我是看了直呼想不到。

---

栈与队列总结

这里理论我就不说了。注意关注栈与队列解决的几类经典问题：
1.括号匹配
2.字符串去重
3.逆波兰表达式问题
4.滑动窗口最大值问题
5.TOPk问题