快速上手LSTM
在文章word embedding是什么，word embedding之前需要做什么？-CSDN博客中我们详细叙述了在word embedding之前我们需要对文本数据进行什么样的处理，现在，基于用所有训练数据构建完词表，我们的文本数据再用普通的前馈神经网络来作为模型是否合适呢？很明显不合适，因为我们的文本数据是时序数据，普通的前馈神经网络并不能处理时序数据。所以我们可以使用专门处理序列数据的循环神经网络。
1. 循环神经网络（RNN）
1.1 什么是RNN
在普通的神经网络中，信息传递是单向的，在很多现实任务中，网络的输入不仅和当前时刻的输入相关，还可能和过去的一段时间输出相关。如时序数据（视频，语音，文本等），而且这些数据长度通常都是不固定的（前馈神经网络要求输入和输出维度固定），循环神经网络解决了这个问题。第一，RNN可以处理变长的输入，第二，RNN可以分析序列的顺序信息。因为它不仅可以接收自身的信息，还可以接收其他神经元的信息。
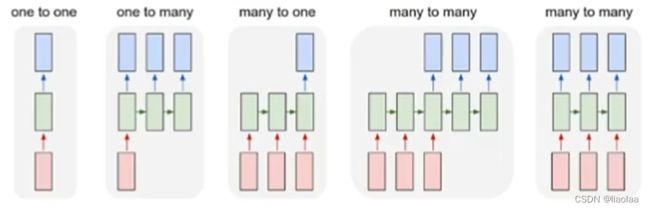
以下有五种不同类型的RNN：
如图，不同任务RNN类型不同，如文本分类属于many to one，文本翻译属于异步的many to many，再如，图像转文字属于one to many，根据视频的每一帧对视频分类属于同步的many to many。
如何理解RNN神经元的输出可以在下一个时间步直接作为输入这句话呢？
我们可以看上面这张图，我们把输入展开![[\, X_{0},\, X_{1},\, X_{2},\,...\,, X_{t-1},\, X_{t},\,]](http://img.e-com-net.com/image/info8/caa1c99e8a334753b923a7b3e7404efe.png){kind=small}
，每个输入是一个不同的时间步上的,每个神经元有两个输入，分别为 
和 
以时间步 
时刻为例，输出两份一模一样的 
一个是当前时间步的输出，一个流向下时刻 
，和 
一起作为神经元的输入。那也就是说，我们之前的所有输入信息是会被携带到下一个神经元中的，即是我们的输出 不仅有包含当前时间步的信息，也有从 
到 的所有信息。通俗的理解就是，它具有记忆能力，它能考虑到当前时刻的信息，也能考虑到之前的信息。
1.2 RNN的缺陷
那按上一段的叙述这么说它应该是具有长期记忆，为什么说它只具有短期记忆呢（RNN长期依赖问题）？长期依赖的问题是RNN的结构造成的，因为他每个状态都包含了上个状态的输出，所以在反向传播的时候就必须进行链式求导，如果我们的输入序列很长，在反向更新参数的时候链式求导必然也会很长，这就容易发生梯度消失或者梯度爆炸。因而RNN的结构必然导致了长期依赖的问题。所以经过很多个时间步，其实对之前距离比较远的时间步的信息的记忆是不太理想的，后来的LSTM解决了这个问题。
1.3 补充
梯度（Gradient）：
给定一个 
个输入 
输出的函数：
它的梯度是偏导数的向量：
![\frac{\partial F}{\partial x} = \left [ \frac{\partial F}{\partial x_{1}},\frac{\partial F}{\partial x_{2}},...,\frac{\partial F}{\partial x_{n}} \right ]](http://img.e-com-net.com/image/info8/efb1a340a69f453991a6a07a38d03f1b.png){kind=small}
梯度下降（Gradient descent）：
给定损失函数 
，学习率
：
求损失函数 对于模型参数
的梯度，代表着对这个参数进行单位大小的改动，损
失函数它变化最快的一个方向。
梯度消失和梯度爆炸（Gradient vanish or explode）：
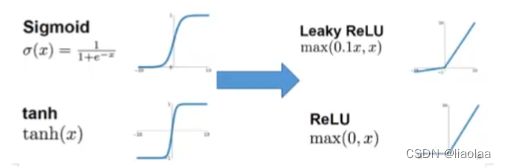
怎么环节梯度爆炸和梯度消失：
1.将激活函数换为ReLU或者是Leaky ReLU；
2.使用改进的梯度优化算法；
3.使用批量规范化（batch normalization）。
2. 长短期记忆网络（LSTM）
2.1 遗忘门
可以通过单元状态
这条流向结合门的结构完成对信息的增加或者删除，由门选择让信息通过或者不通过。
我们将上一时间步的隐状态 
和当前时间步输入 
合并（concat）之后作为lstm单元的输入，乘上权重 
加上偏置 
，再经过sigmoid函数映射为（0,1）区间的数 
与上一时间步的细胞状态
做点乘，来决定历史的信息是否保留或者遗忘的程度。
2.2 输入门
将上一时间步的隐状态 和当前时间步输入 合并（concat）之后作为lstm单元的输入，经过一个sigmoid函数映射为（0,1）区间的数 
，以及经过一个tanh函数生成一个候选状态 
。候选状态 再与 做点乘。
例如，对于“我昨天吃了苹果，今天我想吃菠萝”，遗忘门可以遗忘苹果，同时更新的主语为菠萝。
上一时间步的细胞状态 通过遗忘门的过滤以及输入门的信息补充得到当前时间步的细胞状态 
。即完成将上一时间步的细胞状态 更新为新的细胞状态 。
2.3 输出门
将上一时间步的隐状态 和当前时间步输入 合并（concat）之后作为lstm单元的输入，经过一个sigmoid函数映射为（0,1）区间的数 
，将当前更新完的新细胞状态 经过一个tanh函数与 做点乘得到当前时间步的隐状态 
。即完成决定输出什么样的信息。
总的来说，LSTM最核心的结构在于长期记忆 ，它既能影响每个时刻的输出，又可以根据上一时刻的状态和当前时刻的输入进行调整，因为它不包含任何参数，所以它不受反向传播的影响。
3. 双向长短期记忆网络（Bi LSTM）
单向的RNN只能根据前面的信息推出后面的，但有时候只看前面的词是不够的，可能需要预测的词语和后面的内容也相关，通过双向的lstm我们可以实现让模型不仅能够从前往后看具有记忆，还能从后往前看具有记忆，从而解决这个问题。
如图，在这个隐层中，有一条从前往后的lstm，还有一条从后往前的lstm，我们会将这两个lstm的输出拼接在一起。
4. 快速上手LSTM
首先，通过上面叙述我们知道LSTM的输入和输出分别为：
输入：
, 
,
输出：
, 
,
4.1 torch.nn提供的LSTM
torch.nn.LSTM(input_size, hidden_size, num_layers=1,
bias=True, batch_first=False, dropout=0,
bidirectional=False) input_size：输入数据的形状，即embedding_dim
hidden_size：每一个隐藏层里的每个lstm单元中节点的数量
num_layers：整个RNN架构中隐藏层的层数
batch_first：默认为False，输入数据必须为 [seq_len, batch_size, feature]，若为True，则输入数据必须为 [batch_size, seq_len, feature]
dropout：默认为0，dropout是训练中使部分参数随机失活，提高训练速度的同时能够解决过拟合问题。这里是对最后一层的每个lstm单元输出进行dropout
bidirectional：若为 True，则使用双向 LSTM，默认为 False
即：
output, (h_n, c_n) = lstm(input, (h_0, c_0))注意：在实例化torch.nn.LSTM的时候若没传入初始隐藏状态h_0和初始记忆状态c_0,会默认将这两个值置为全0。
4.2 lstm使用细节
我们构建一个batch的数据，即batch_size为10，每个句子的长度为30个单词，即seq_len为30。
data = torch.randint(low=0, high=100, size=[batch_size,seq_len]) # [10, 30]指定稠密向量长度为20，即embedding_dim为20，词表大小（词表中单词数量）为vocab_size为100，即vocab_size = 100。将数据经过embedding处理得到input_embeded，形状为[batch_size, seq_len, embedding_dim] -> [10, 30, 20] 。
embedding = nn.Embedding(vocab_size,embedding_dim)
input_embeded = embedding(data) # [10, 30, 20]将准备好的数据 input_embeded 作为模型的输入。指定每一个隐藏层里的lstm单元数量为18，即 hidden_size为18。指定隐藏层层数为1，即num_layer为1。并使用单向lstm，因为batch_size在第一维度，我们指定batch_first=True。
lstm = nn.LSTM(input_size=embedding_dim, hidden_size=hidden_size,
num_layers=num_layer, bidirectional=False,
batch_first=True)
output,(h_n,c_n) = lstm(input_embeded) # 会自动帮我们生成初始状态的(h_0,c_0)
print(output.shape) # torch.Size([10, 30, 18])
# 即 [batch_size, seq_len, hidden_size*num_directions]
# 把每个时间步的结果都在seq_len这个维度拼接
print("--------------------------------------")
print(h_n.shape) # torch.Size([1, 10, 18])
# 即 [num_layer*num_direction, batch_size, hidden_size]
#
# h_n把不同层的隐藏状态在第0个纬度拼接起来
print("--------------------------------------")
print(c_n.shape) # torch.Size([1, 10, 18])
# 即 [num_layer*num_direction, batch_size, hidden_size]
# 和h_n一样4.3 模型架构
模型架构大致为上图，这是一个只有一层隐层的双向lstm，在 4.3 节中我们指定一层的单向lstm，应为下图所示，
所以在hidden_layer 中会有 30 个 
单元，每个时间步都会输出一个 
,这个输出其实就是这个时间步的 单元输出的 
。注意，模型只取最后一层的输出，作为我们的output，在这里只有一层隐层，所以直接取这一层的输出，把每个时间步的输出拼在一起。
可以通过一下代码验证：
# 获取最后一个timestep的输出，即w30的输出
last_output = output[:,-1,:] # 取seq_len的最后一个词元
# 获取最后一次hidden_state 即 拿最上面一层的（在两层lstm）
last_hidden_state = h_n[-1,:,:]
print(last_hidden_state == last_output)tensor([[True, True, True, True, True, True, True, True, True, True, True, True,
True, True, True, True, True, True],
[True, True, True, True, True, True, True, True, True, True, True, True,
True, True, True, True, True, True],
[True, True, True, True, True, True, True, True, True, True, True, True,
True, True, True, True, True, True],
[True, True, True, True, True, True, True, True, True, True, True, True,
True, True, True, True, True, True],
[True, True, True, True, True, True, True, True, True, True, True, True,
True, True, True, True, True, True],
[True, True, True, True, True, True, True, True, True, True, True, True,
True, True, True, True, True, True],
[True, True, True, True, True, True, True, True, True, True, True, True,
True, True, True, True, True, True],
[True, True, True, True, True, True, True, True, True, True, True, True,
True, True, True, True, True, True],
[True, True, True, True, True, True, True, True, True, True, True, True,
True, True, True, True, True, True],
[True, True, True, True, True, True, True, True, True, True, True, True,
True, True, True, True, True, True]])隐层中的双向lstm是怎么样的呢？
其实可以把一层双向lstm看成是两层，第一层是正向lstm，第二层是反向lstm，同样我们的输出也只会取到第二层的输出作为我们的output。
# 如果是有反向怎么获取？
last_hidden_state = h_n[-1,:,:] # 输出从上到下依次拿到第一层的正向
# 第一层的反向
# 输出从上到下依次拿到第二层的正向
# 第二层的反向
# ...4.4 附上完整代码
# LSTM使用示例
import torch.nn as nn
import torch
batch_size = 10
seq_len = 30
vocab_size = 100
embedding_dim = 20
hidden_size = 18 #隐层中每个lstm单元中节点个数
num_layer = 1 # 隐层
# 构造一个batch的数据
data = torch.randint(low=0, high=100, size=[batch_size,seq_len]) # [10, 30]
# 数据经过embedding的处理
embedding = nn.Embedding(vocab_size,embedding_dim)
input_embeded = embedding(data) # [10, 30, 20]
# embedding后的数据传入lstm
lstm = nn.LSTM(input_size=embedding_dim, hidden_size=hidden_size,
num_layers=num_layer, bidirectional=False,
batch_first=True)
output,(h_n,c_n) = lstm(input_embeded) # 会自动帮我们生成初始状态的(h_0,c_0)
print(output.shape) # torch.Size([10, 30, 18])
# 即 [batch_size, seq_len, hidden_size*num_directions]
# 把每个时间步的结果都在seq_len这个维度拼接
print("--------------------------------------")
print(h_n.shape) # torch.Size([1, 10, 18])
# 即 [num_layer*num_direction, batch_size, hidden_size]
#
# h_n把不同层的隐藏状态在第0个纬度拼接起来
print("--------------------------------------")
print(c_n.shape) # torch.Size([1, 10, 18])
# 即 [num_layer*num_direction, batch_size, hidden_size]
# 和h_n一样
# 获取最后一个timestep的输出，即w30的输出
last_output = output[:,-1,:] # 取seq_len的最后一个词元
# 获取最后一次hidden_state 即 拿最上面一层的（在两层lstm）
last_hidden_state = h_n[-1,:,:]
print(last_hidden_state == last_output)
# 如果是有反向怎么获取？
last_hidden_state = h_n[-1,:,:] # 输出从上到下依次拿到第一层的正向
# 第一层的反向
# 输出从上到下依次拿到第二层的正向
# 第二层的反向
# ...