BZOJ 1502 月下柠檬树(simpson积分)
题目链接:http://61.187.179.132/JudgeOnline/problem.php?id=1502
题意:给出如下一棵分层的树,给出每层的高度和每个面的半径。光线是平行的,与地面夹角alpha。求树在地面上投影的面积。
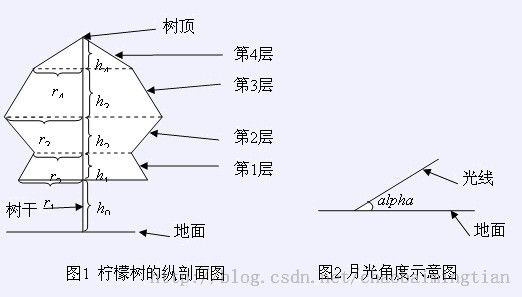
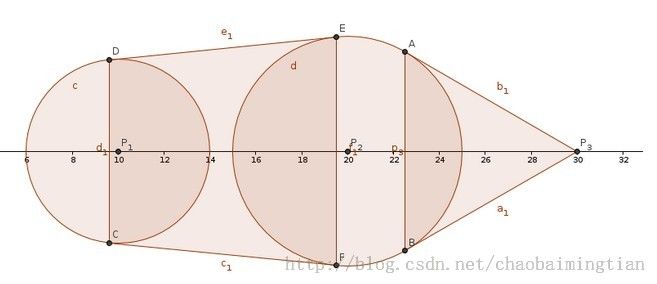
思路:样例的投影如下,所有面积就是这些的面积交,包括一些圆、等腰梯形。首先要计算出等腰梯形,也就是两个圆公切线与圆的交点。之后就是simpson公式:
simpson(L,R)表示图形在x=L,x=R与x轴围成图形的面积。若simpson(L,mid)+simpon(mid,R)=simpson(L,R),则直接返回simpson(L,R),否则递归计算rsimpson(L,R)。计算时我们调用的是rsimpson(L,R)。
struct point
{
double x,y;
void print()
{
printf("%lf %lf\n",x,y);
}
};
int sgn(double x)
{
if(x>EPS) return 1;
if(x<-EPS) return -1;
return 0;
}
point a[N],s[N],e[N];
int n;
double ang;
void cal(point &s,point &e,point a,point b)
{
if(sgn(a.y-b.y)==0)
{
s=a; e=b;
return;
}
double x0=a.x-a.y*(b.x-a.x)/(b.y-a.y);
double SinAng=a.y/(a.x-x0);
s.x=a.x-a.y*SinAng;
s.y=sqrt(sqr(a.y)-sqr(s.x-a.x));
e.x=b.x-b.y*SinAng;
e.y=sqrt(sqr(b.y)-sqr(e.x-b.x));
}
double f(double x)
{
double y=0;
int i;
for(i=1;i<=n+1;i++) if(fabs(x-a[i].x)<=a[i].y) y=max(y,sqrt(sqr(a[i].y)-sqr(x-a[i].x)));
for(i=1;i<=n;i++) if(a[i+1].x-a[i].x-fabs(a[i+1].y-a[i].y)>EPS&&s[i].x<=x&&x<=e[i].x)
{
y=max(y,s[i].y+(e[i].y-s[i].y)*(x-s[i].x)/(e[i].x-s[i].x));
}
return y;
}
double DFS1(double L,double R)
{
return (f(L)+4*f((L+R)/2.0)+f(R))*(R-L)/6.0;
}
double DFS(double L,double R)
{
double mid=(L+R)/2.0;
double x=DFS1(L,R),y=DFS1(L,mid),z=DFS1(mid,R);
if(fabs(x-y-z)<EPS) return y+z;
return DFS(L,mid)+DFS(mid,R);
}
int main()
{
RD(n); RD(ang); ang=1.0/tan(ang);
int i;
double h=0;
FOR1(i,n+1) RD(a[i].x),h+=a[i].x,a[i].x=h*ang;
FOR1(i,n) RD(a[i].y); a[i+1].y=0;
double L=a[1].x,R=a[n+1].x;
FOR1(i,n)
{
L=min(L,a[i].x-a[i].y);
R=max(R,a[i].x+a[i].y);
if(a[i+1].x-a[i].x-fabs(a[i+1].y-a[i].y)>EPS)
{
cal(s[i],e[i],a[i],a[i+1]);
}
}
PR(2*DFS(L,R));
}