算法系列--滑动窗口与双指针

简述个人理解滑动窗口与双指针：

双指针：以r为基础指针并根据题目要求来移动l或者保持l不动，同时ans由每一步的r-l来更新。

滑动窗口：以l为基础指针，并且l~r看做一个窗口，r不断右移，根据题目要求来右移一次l或者保持l不动，特点是r-l始终不减，ans为最终的r-l

区别：双指针算法当需要移动l指针时，可能移动多个单位以满足要求。而滑动窗口算法当需要移动l指针时，每次必定只移动一个单位！

---

算法选择：
求最短长度类似题目：双指针
求最长长度类似题目：双指针 or 滑动窗口

---

题目一

LC 1004. 最大连续1的个数 III

题目描述：
给定一个由若干 0 和 1 组成的数组 A，我们最多可以将 K 个值从 0 变成 1 。
返回仅包含 1 的最长（连续）子数组的长度。

题解：

• 双指针算法

本质是找到最长的一个子数组，满足该子数组中元素0的个数不超过K个
双指针模拟，r指针右移并统计当前l~r之间0的个数cnt。当cnt > K时，需要不断右移l指针，直到满足l’~r之间0的个数再次 <= K。
针对每一个r，都有对应的l，此时r-l即为以r结尾的满足要求子数组的长度。
ans即为所有r-l的最大值。

class Solution {
public:
    int longestOnes(vector<int>& A, int K) {
        int n = A.size(), l = 0, r = 0, cnt = 0;
        int ans = 0;
        while(r < n)
        {
            if(A[r] == 0)   cnt++;
            while(cnt > K)      //针对右边界，来调整满足条件的最小左边界
            {
                if(A[l] == 0)   cnt--;
                l++;
            }
            ans = max(ans, r - l + 1);
            r++;
        }
        return ans;
    }
};

• 滑动窗口算法

针对初始l，当第一次不满足条件时，说明此时r~l之间0的个数 > K。那么(针对l指针的最大)ans当前记为r-l。此时需要将l指针右移一位，并更新cnt，同时r右移
有如下来两种情况：

1. 如果右移完之后，针对l的子数组最大长度(从事实来看)大于当前r-l，只需要下次移动r即可。
2. 如果针对l的子数组最大长度小于当前r-l，由于我们需要最长子数组长度，所以该种情况我们不需要考虑。

对于情况2，不需要考虑在代码实现上如何表示？
当忽略指针以当前指针l为其实的子数组，只需要让l+1即可。那么考虑if条件的成立情况：
当情况2发生，一定有cnt > K， 那么if一定成立，故l+1可以实现。

最终答案：
全程下来，r每次都右移，而l可能移动可能不动。r-l始终由第一次的r-l撑着，只会变大，不会变小。
还是由于答案求最长子数组的特点，当r到达n-1时，l停下，并不需要对l+1~n-1之间的数组进行判断。就算l+1 ~n-1全长满足条件，长度也小于当前r-l，。

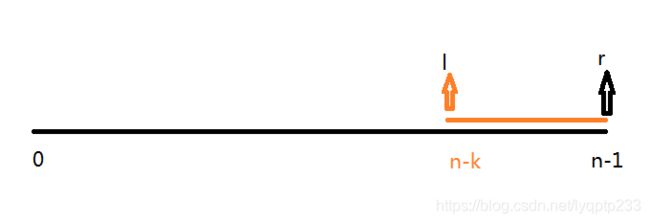
class Solution {
public:
    int longestOnes(vector<int>& A, int K) {
        int n = A.size(), l = 0, r = 0, cnt = 0;
        while(r < n)
        {
            if(A[r] == 0)   cnt++;
            if(cnt > K)
            {
                if(A[l++] == 0)     cnt--;
            }
            r++;
        }
        return r - l;
    }
};

从另一个角度看本题，转化为求和小于等于K的最长子数组长度：
定义：把0替换为1需要1个val，1替换为1需要0val。(相当于对每个数取反)
例如：
原： 1 1 1 0 0 0 1 1 1 1 0
tar： 1 1 1 1 1 1 1 1 1 1 1
var：0 0 0 1 1 1 0 0 0 0 1
自然问题转化为前述问题。

题目二

LC 424. 替换后的最长重复字符

题目描述：
给你一个仅由大写英文字母组成的字符串，你可以将任意位置上的字符替换成另外的字符，总共可最多替换 k 次。在执行上述操作后，找到包含重复字母的最长子串的长度。注意：字符串长度 和 k 不会超过 10⁴。

题解：

• 滑动窗口算法

思路同上一题滑动窗口解法，重点分析如上类似情况2：
当对于上一次刚移动完的l+1，如果对应的maxlen’小于maxlen(上一次循环)，应该忽略此l，即让l再次+1.
如何实现此操作？
如果发生情况2，真实情况下是maxlen’，一定会导致if成立，进而实现l+1
那么maxlen在如下代码更新过程中却保持当前maxlen，所以if条件还会在此成立！
这里是一种巧妙的优化。

class Solution {
public:
    int characterReplacement(string s, int k) {
        int n = s.size();
        int l = 0, r = 0;
        vector<int> cnt(26);
        int maxlen = 0;
        while(r < n)
        {
            maxlen = max(maxlen, ++cnt[s[r] - 'A']);
            if(r - l + 1 - maxlen > k)     cnt[s[l++] - 'A']--;
            r++;
        }
        return r - l;
    }
};

题目三

LC 1208. 尽可能使字符串相等

问题描述：给你两个长度相同的字符串，s 和 t。
将 s 中的第 i 个字符变到 t 中的第 i 个字符需要 |s[i] - t[i]| 的开销（开销可能为 0），也就是两个字符的 ASCII 码值的差的绝对值。
用于变更字符串的最大预算是 maxCost。在转化字符串时，总开销应当小于等于该预算，这也意味着字符串的转化可能是不完全的。
如果你可以将 s 的子字符串转化为它在 t 中对应的子字符串，则返回可以转化的最大长度。如果 s 中没有子字符串可以转化成 t 中对应的子字符串，则返回 0。

问题简化：找出最长子数组满足元素和小于等于maxCost
（数组元素为|s[i] - t[i]|）

题解：

• 滑动窗口算法

思路同上上一题滑动窗口解法，重点分析如上类似情况2：

1. 当对于上一次刚移动完的l+1，如果sum’小于maxCost，说明对于左边界l+1的子数组最大右边界比当前r大，仍然待更新r， l不动。
2. 如果sum’大于maxCost，说明上一次去掉l元素，sum仍然不满足条件，即l+1~r的元素和超额，但是此时长度已经小于上一次的ans，则忽略此l+1对应的子数组，if条件成立，l+1。

class Solution {
public:
    int equalSubstring(string s, string t, int maxCost) {
        int n = s.size(), l = 0, r = 0, ans = 0, sum = 0;
        while(r < n)
        {
            sum += abs(s[r] - t[r]);
            if(sum > maxCost)   sum -= abs(s[l] - t[l++]);
            r++;
        }
        return r - l;
    }
};

题目四

LC 1493. 删掉一个元素以后全为 1 的最长子数组

问题描述：
给你一个二进制数组 nums ，你需要从中删掉一个元素。
请你在删掉元素的结果数组中，返回最长的且只包含 1 的非空子数组的长度。
如果不存在这样的子数组，请返回 0 。

问题简化：找出最长子数组满足数组中元素0的个数小于等于1
如果把数组取反，问题又变为：在新数组中找出最长子数组满足元素和小于等于1

题解：

• 滑动窗口算法
  直接套用 1004题目代码，最终返回答案再-1即可。

class Solution {
public:
    int longestSubarray(vector<int>& A) {
        int n = A.size(), l = 0, r = 0, cnt = 0;
        while(r < n)
        {
            if(A[r] == 0)   cnt++;
            if(cnt > 1)
            {
                if(A[l++] == 0)     cnt--;
            }
            r++;
        }
        return r - l - 1;
    }
};

• 双指针算法

用l，r分别记录某一个0前后连续1的个数，遇到0时，ans用l+r更新。

class Solution {
public:
    int longestSubarray(vector<int>& nums) {
        int n = nums.size(), l = 0, r = 0;
        int ans = 0;
        for(auto x : nums)
        {
            if(x == 0)  
            {
                ans = max(ans, l + r);
                l = r;
                r = 0;
            }
            else    r++;
        }
        ans = max(ans, l + r);
        return ans == n ? n - 1 : ans;
    }
};

题目五

LC 3. 无重复字符的最长子串

题目描述：
给定一个字符串，请你找出其中不含有重复字符的 最长子串 的长度。

题解：

• 双指针算法

枚举r，当遇到某一个s[r]数量大于1，移动l指针，直到数量变为1为止。
ans在每次循环中不断更新。

class Solution {
public:
    int lengthOfLongestSubstring(string s) {
        unordered_map<char, int> hash;
        int n = s.size(), ans = 0;
        int l = 0, r = 0;
        while(r < n)
        {
            hash[s[r]]++;
            while(hash[s[r]] > 1)    hash[s[l++]]--;
            ans = max(ans, r - l + 1); 
            r++;
        }
        return ans;
    }
};

题目六

LC 209. 长度最小的子数组

问题描述：
给定一个含有 n 个正整数的数组和一个正整数 target 。
找出该数组中满足其和 ≥ target 的长度最小的连续子数组 并返回其长度。如果不存在符合条件的子数组，返回 0 。

题解：

• 双指针算法

枚举r，当sum >= tar，可以移动l指针，直到sum < tar为止。
ans在内层循环中不断更新。
注意：只有能移动l指针，才说明这一段sum >= tar, 才能在此条件下更新答案。

---

对比题目一的问题转化：和小于等于K的最长子数组长度
本题：和大于等于K的最短子数组长度

---

class Solution {
public:
    int minSubArrayLen(int s, vector<int>& nums) {
        int n = nums.size(), l = 0, r = 0;
        int sum = 0, ans = 0x3f3f3f3f;
        while(r < n)
        {
            sum += nums[r];
            while(sum >= s)
            {
                ans = min(ans, r - l + 1);
                sum -= nums[l++];
            }
            r++;
        }
        return ans == 0x3f3f3f3f ? 0 : ans;
    }
};

题目七

LC 76. 最小覆盖子串

题目描述：
给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串，则返回空字符串 “” 。
注意：如果 s 中存在这样的子串，我们保证它是唯一的答案。

题解：

• 双指针算法

事先统计t中各字符数量，枚举r，当l对应的字符在l~r之间数量大于t中数量，移动l。注意：需要判断当前范围内各字符是否涵盖t中字符，只有确认涵盖之后，才能更新ans，并记录l位置(答案要求返回字符串)

class Solution {
public:
    string minWindow(string s, string t) {
        int m = s.size(), n = t.size();
        unordered_map<char, int> hash, cnt;
        for(auto& c : t)    hash[c]++;
        int l = 0, r = 0, ans = m + 1, idx = -1;
        bool tt = false;
        while(r < m)
        {
            cnt[s[r++]]++;
            while(cnt[s[l]] > hash[s[l]])   cnt[s[l++]]--;
            bool flag = true;
            if(!tt)
            {
                for(auto& [c, k] : hash)
                {
                    if(cnt[c] < k)  
                    {
                        flag = false;
                        break;
                    }
                }                
            }
            if(flag && ans > r - l)    
            {
                tt = true;
                ans = r - l;
                idx = l;
            }
        }
        if(idx == -1)   return "";
        string res = s.substr(idx, ans);
        return res;
    }
};

题目八

LC 438. 找到字符串中所有字母异位词

题目描述：
给定一个字符串 s 和一个非空字符串 p，找到 s 中所有是 p 的字母异位词的子串，返回这些子串的起始索引。
字符串只包含小写英文字母，并且字符串 s 和 p 的长度都不超过 20100。

题解：

• 双指针算法

类似上题，事先统计p的各字符数量。枚举r，当s[r]的数量超过p中数量时，移动l。res取决于区间长度 == p.size()
时刻保持l~r中各字符数量严格小于等于p中对应字符数量.
只有当l~r中各字符数量严格等于p中对应字符数量.，if才会成立！
而不会出现某字符数量少，另一种字符数量多，加起来新长度相等的情况。

class Solution {
public:
    vector<int> findAnagrams(string s, string p) {
        int m = s.size(), n = p.size();
        if(m < n)   return {};
        vector<int> cnt(26), key(26);
        for(auto& c : p)    key[c - 'a']++;
        int l = 0, r = 0;
        vector<int> res;
        while(r < m)
        {
            int idx = s[r++] - 'a';
            cnt[idx]++;
            while(cnt[idx] > key[idx])    cnt[s[l++] - 'a']--;
            if(r - l == n)  res.push_back(l);
        }
        return res;
    }
};

题目九

LC 992. K 个不同整数的子数组

题目描述：
给定一个正整数数组 A，如果 A 的某个子数组中不同整数的个数恰好为 K，则称 A 的这个连续、不一定独立的子数组为好子数组。
（例如，[1,2,3,1,2] 中有 3 个不同的整数：1，2，以及 3。）
返回 A 中好子数组的数目。

题解：

• 双指针算法

本质：找到一个子数组，使得子数组中字符种类数为K
细节：
对于一个A[r], 有l1, l2满足
A[l1]是A[r]最长的左边界,且A[l1~r]有k个不同整数
A[l2]是A[r]最长的左边界,且A[l2~r]有k-1个不同整数
当l2左移一个长度之后，此时A[l2~r]之间便有k个不同整数
即l2-1：是A[r]最短的左边界,且A[l2-1~r]有k个不同整数
则A[r]对应的ans为：l2 - l1
只需要对数组模拟两遍l, r的操作，对应不同阈值分别为k, k - 1.

class Solution {
public:
    int subarraysWithKDistinct(vector<int>& A, int K) {
        int n = A.size();
        int l1 = 0, l2 = 0, r = 0;
        unordered_map<int, int> hash1, hash2;
        int ans = 0;
        while(r < n)
        {
            hash1[A[r]]++, hash2[A[r]]++;
            while(hash1.size() > K)
            {
                hash1[A[l1]]--;
                if(hash1[A[l1]] == 0)    hash1.erase(A[l1]);  
                l1++;                  
            }
            while(hash2.size() > K - 1)
            {
                hash2[A[l2]]--;
                if(hash2[A[l2]] == 0)    hash2.erase(A[l2]);    
                l2++;                
            }
            if(hash1.size() == K && hash2.size() == K - 1)  ans += l2 - l1;
            r++;
        }
        return ans;
    }
};

题目十

LC 904. 水果成篮

题目描述：在一排树中，第 i 棵树产生 tree[i] 型的水果。
你可以从你选择的任何树开始，然后重复执行以下步骤：
把这棵树上的水果放进你的篮子里。如果你做不到，就停下来。
移动到当前树右侧的下一棵树。如果右边没有树，就停下来。
请注意，在选择一颗树后，你没有任何选择：你必须执行步骤 1，然后执行步骤 2，然后返回步骤 1，然后执行步骤 2，依此类推，直至停止。
你有两个篮子，每个篮子可以携带任何数量的水果，但你希望每个篮子只携带一种类型的水果。
用这个程序你能收集的水果树的最大总量是多少？

题解：

本质：求最长子数组，并且该子数组中只包含两种元素

• 双指针算法

class Solution {
public:
    int totalFruit(vector<int>& tree) {
        unordered_map<int, int> hash;
        int n = tree.size();
        int l = 0, r = 0, ans = 1;
        while(r < n)
        {
            hash[tree[r]]++;
            while(hash.size() > 2)
            {
                hash[tree[l]]--;
                if(hash[tree[l]] == 0)  hash.erase(tree[l]);
                l++;
            }
            r++;
            ans = max(ans, r - l);
        }
        return ans;
    }
};

• 滑动窗口算法

class Solution {
public:
    int totalFruit(vector<int>& tree) {
        unordered_map<int, int> hash;
        int n = tree.size();
        int l = 0, r = 0；
        while(r < n)
        {
            hash[tree[r]]++;
            if(hash.size() > 2)
            {
                hash[tree[l]]--;
                if(hash[tree[l]] == 0)  hash.erase(tree[l]);
                l++;
            }
            r++;
        }
        return r - l;
    }
};

题目十一

LC 1358. 包含所有三种字符的子字符串数目

题目描述：
给你一个字符串 s ，它只包含三种字符 a, b 和 c 。
请你返回 a，b 和 c 都 至少 出现过一次的子字符串数目。

题解：

• 双指针算法

枚举r，当第一个r使得0~r内含有a， b， c元素时，再以后每一个以r为右边界的子数组的z最小左边界都为下标0
而最大左边界即：如果当前l对应的字符出现次数大于1，就右移l，直到某个位置，l对应字符出现唯一一次。此时l为最大左边界。

class Solution {
public:
    int numberOfSubstrings(string s) {
        int cnt[3] = {0};
        int l = 0, r = 0, n = s.size();
        int ans = 0;
        while(r < n)
        {
            cnt[s[r] - 'a']++;
            while(cnt[s[l] - 'a'] > 1)      cnt[s[l++] - 'a']--;
            if(cnt[0] && cnt[1] && cnt[2])  ans += l + 1;
            r++;
        }
        return ans;
    }
};