【算法 - 动态规划】原来写出动态规划如此简单！
从本篇开始，我们就正式开始进入 动态规划 系列文章的学习。
本文先来练习两道通过 建立缓存表 优化解题过程的题目，对如何将 递归函数 修改成 动态规划 的流程有个基本的熟悉。
基本流程
- 用最简单的想法完成题目要求的 递归 函数；
- 定义明确 递归函数 的功能！！！
分析是否存在 重叠子问题 ，即能否进行 剪枝 操作；
建立 数组或集合 缓存，寻找 状态转移方程 ，完成动态规划。
不太懂没关系，相信通过下面两道题目的练习就能找到感觉。
走到目标位置
假设有 N 个位置从左到右排成一排，记为 1 ~ N 。一个机器人开始在 start 位置上（1 ≤ start ≤ N），可以往左或者往右走，规定机器人只能走 K 步，最终能来到 aim（1 ≤ aim ≤ N） 位置的方法有多少种。
注意：
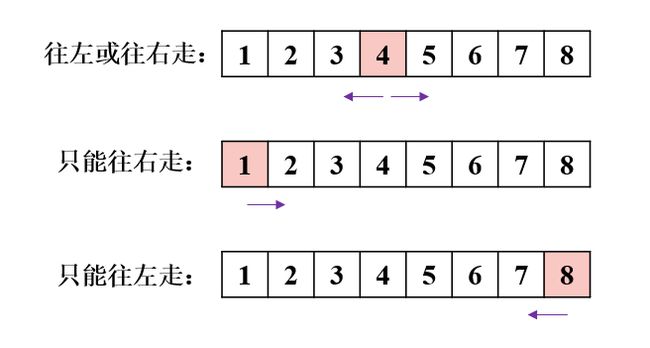
若机器人在 1 位置，下一步只能向右走到 2 位置；
若机器人在 N 位置，下一步只能向左走到 N-1 位置。
递归的准备
定义递归函数的功能： 从当前位置出发，走 k 步到达目的地，共有多少种行走的方法。
思考递归需要的参数： 当前位置、目标位置、需要走的步数、能行走的范围。
明确递归的边界条件： 如果当前需要走的步数为 0 ，且此时正好在目标位置，即找到了一种有效的行走方法；反之没有找到。
思路
寻找相同类型子问题：
- 若机器人当前在 1 号位置 ，只能 往右走 ，因此走 k 步的答案，应该和在 2 号位置上走 k-1 步的答案一样。
- 若机器人当前在 N 号位置 ，只能 往左走 ，因此走 k 步的答案，应该和在 N-1 号位置上走 k-1 步的答案一样。
- 若机器人当前在 中间位置 ，因此走 k 步的答案，应该是前一个位置走 k-1 步与后一个位置走 k-1 步的总和。
代码
public static int ways(int start, int K, int aim, int N) {
if (N < 2 || start < 1 || start > N || aim < 1 || aim > N || K < 1) {
return -1;
}
// 调用递归函数
return process(start, K, aim, N);
}
private static int process(int cur, int remain, int aim, int N) {
// 已经来到目标位置，且步数为 0。
if (remain == 0) {
return cur == aim ? 1 : 0;
}
// 到了最左边
if (cur == 1) {
return process(2, remain - 1, aim, N);
}
// 到了最右边
if (cur == N) {
return process(N - 1, remain - 1, aim, N);
}
// 在中间位置
return process(cur - 1, remain - 1, aim, N) + process(cur + 1, remain - 1, aim, N);
}
相信上面的代码很容易看懂 ~
思考上面的递归过程，画出部分递归调用的过程图：
例如，当前机器人位置在 4 号位置还有 5 步要走，用 4,5 表示。
- 若往左走，来到 3 号位置，还有 4 步要走，用
3,4表示； - 若往右走，来到 5 号位置，还有 4 步要走，用
5,4表示；
以此类推，递归调用图中出现了相同的 4,3 ，即出现了 重叠子问题 ，因此就有必要进行 缓存优化 。
接下来我们使用 缓存 的方法优化该递归过程:
思路
写完递归的代码之后，再来修改缓存代码就变的非常简单。
考虑到递归传递的参数中 process(int cur, int remain, int aim, int N) ，只有 cur, remain 两个参数会发生变化，因此，就可以构造一个 以这两个参数为变量 的 二维 dp 数组 。
-
- 思考两个变量的取值范围，构造数组长度。由于
1 ≤ cur ≤ N,0 ≤ remain ≤ K，因此将数组长度设置为 dp[N+1][K+1] 。
- 思考两个变量的取值范围，构造数组长度。由于
-
- 将 dp 数组值设置为 -1。若计算过该位置该步长的情况，就更新 dp 中对应位置的值。因此，若值不为 -1 ，说明之前计算过，可以直接获取，达到了剪枝的目的。
-
- 更新的方法是，先用变量
ans记录下情况数，在退出本层递归时更新 dp 表。
- 更新的方法是，先用变量
缓存优化代码
// dp缓存法
public static int ways(int start, int K, int aim, int N) {
if (N < 2 || start < 1 || start > N || aim < 1 || aim > N || K < 1) {
return -1;
}
int[][] dp = new int[N + 1][K + 1];
for (int i = 0; i <= N; i++) {
for (int j = 0; j <= K; j++) {
dp[i][j] = -1;
}
}
return process(start, K, aim, N, dp);
}
private static int process(int cur, int remain, int aim, int N, int[][] dp) {
if (dp[cur][remain] != -1) {
return dp[cur][remain];
}
int ans = 0;
if (remain == 0) {
ans = cur == aim ? 1 : 0;
} else if (cur == 1) {
ans = process(2, remain - 1, aim, N, dp);
} else if (cur == N) {
ans = process(N - 1, remain - 1, aim, N, dp);
} else {
ans = process(cur - 1, remain - 1, aim, N, dp) + process(cur + 1, remain - 1, aim, N, dp);
}
dp[cur][remain] = ans;
return ans;
}
看懂思路之后，上面的代码也很容易看懂！
因为该递归是从原始问题开始，逐步分解为子问题的，因此称为 自顶向下 的 备忘录 递归解法。
优化后的代码虽然使用 dp 数组进行了一定量的 剪枝 操作，但这并不是最终 动态规划版本 的代码，接下来，我们通过画图来寻找真正的 状态转移方程:
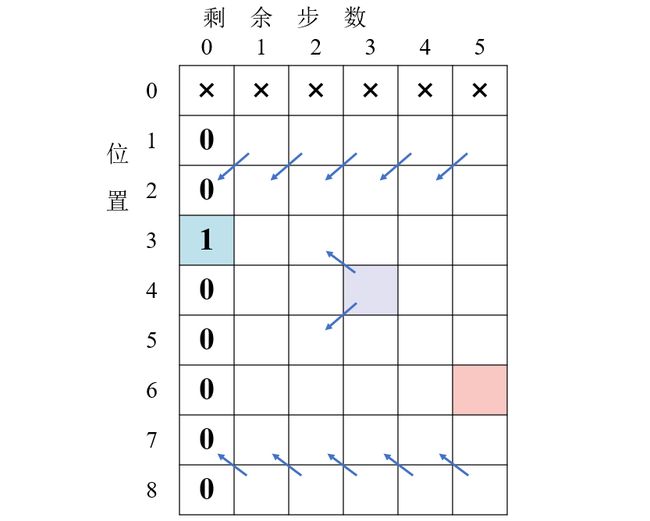
假设 N = 8，步数 K = 5，起始位置 start = 6，目标位置 aim = 3。由此可以画出初始 dp 表为：（坐标 用( 位置 , 剩余步数 )表示；表中的 数字大小 表示到达目标位置的 方法数 ）
红色代表初始位置 (6,5)，蓝色代表最终目标位置 (3,0)。
没有 0 号位置，因此第 0 列无效，用 × 表示。
根据递归函数中代码逻辑发现：
- 当步数为
0时，只有目标位置的值为 1 ，其余均为 0。
// 已经来到目标位置，且步数为 0。
if (remain == 0) {
return cur == aim ? 1 : 0;
}
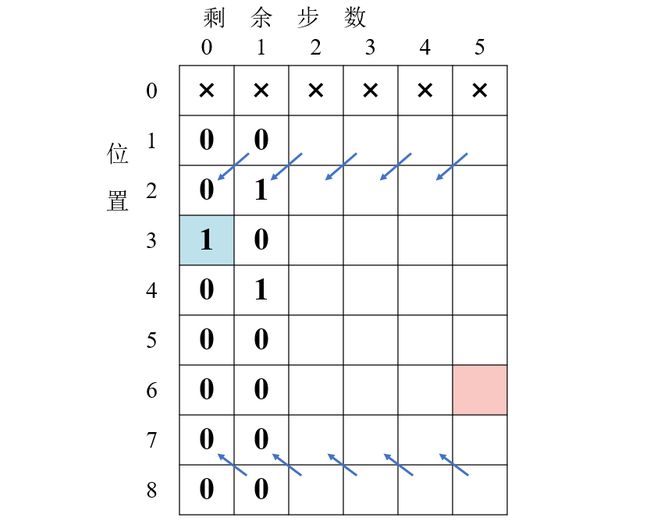
- 当当前位置
cur为 1 时，依赖 2 号位置，步数小 1 的信息（向左下依赖）。当当前位置cur为 N 时，依赖 N - 1 号位置，步数小 1 的信息（向左上依赖）。
// 到了最左边
if (cur == 1) {
return process(2, remain - 1, aim, N);
}
// 到了最右边
if (cur == N) {
return process(N - 1, remain - 1, aim, N);
}
- 当在中间位置时，共同依赖前后一个位置，步数均小 1 的信息（向左上和左下依赖）。
// 在中间位置
return process(cur - 1, remain - 1, aim, N) + process(cur + 1, remain - 1, aim, N);
由此可以在图中标注依赖关系方向。
根据图中的依赖方向很容易一行一行的填出所有答案：
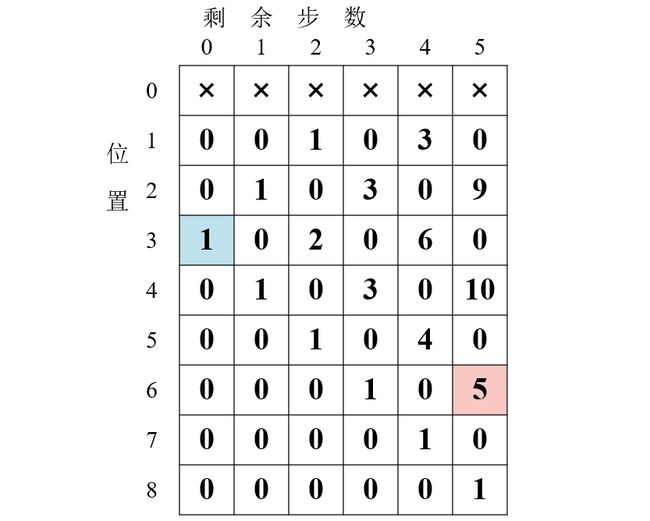
表中坐标 (6,5) 的值是 5 ，说明初始在位置 6 走 5 步，走到位置 3 共有 5 种走法。
这张表就是动态规划表！
现在我们就通过代码模拟刚才的填表过程：
// 动态规划
public static int ways3(int start, int K, int aim, int N) {
if (N < 2 || start < 1 || start > N || aim < 1 || aim > N || K < 1) {
return -1;
}
int[][] dp = new int[N + 1][K + 1];
dp[aim][0] = 1;
for (int remain = 1; remain <= K; remain++) {
dp[1][remain] = dp[2][remain - 1];
for (int cur = 2; cur < N; cur++) {
dp[cur][remain] = dp[cur - 1][remain - 1] + dp[cur + 1][remain - 1];
}
dp[N][remain] = dp[N - 1][remain - 1];
}
return dp[start][K];
}
代码解释
第一列只有dp[aim][0]位置为 1 ，其余位置均为 0 。之后从上往下从左到右，一列一列的填写：
- for 循环中，把第一行和最后一行单独填写，即分别向左下和左上依赖。中间行分别依赖左上和左下部分的值。
- 最终返回要求的目标位置的
dp[start][K]的值。
因为该方法是从最小的子问题开始逐步求解，因此称为 自底向上的动态规划。
上面这道题使用了 一张 dp 表 完成了自底向上的动态规划，下面我们增加点难度，来看一道使用 两张 dp 表 才能完成的动态规划题目。
纸牌博弈问题
牛客网链接-纸牌博弈问题：给定一个整型数组arr，代表数值不同的纸牌排成一条线。玩家 A 、B依次拿走每张纸牌，规定玩家 A 先拿，玩家 B 后拿，每个玩家每次只能拿走最左和最右侧的纸牌，玩家A和玩家B绝顶聪明。请返回最后的获胜者的分数。
例如：
返回获胜者的答案应该是：1+100=101
递归的准备
定义递归函数的功能：
- 如果是 先手 则能够获得的最大值；
- 如果是 后手 则能够获得的最大值。
思考递归需要的参数： 当前剩余的整个数组、两个边界 L 和 R 。
明确递归的边界条件： 只剩下一张牌时，如果是先手，获得该牌的数值，如果是后手，获得数值为 0 。
思路
- 如果是先手：
- 拿了左侧 L ，最终获得的分数 = 此时左侧 L 的分数 + 剩下的部分做为后手时拿到的分数。
- 拿了右侧 R ，最终获得的分数 = 此时右侧 R 的分数 + 剩下的部分做为后手时拿到的分数。
- 此时应该取两种情况的 最大值 作为最终的抉择。
- 如果是后手：
- 此时 [L, R] 上的抉择权就不在自己手中了（因为此时先手得先拿）。
- 因此，作为后手的自己只能获得先手拿过之后的最小值（先手肯定不会让你拿最大了！又不傻~）
代码
public static int win(int[] arr) {
if (arr == null || arr.length == 0) {
return 0;
}
int first = f(arr, 0, arr.length - 1);
int after = g(arr, 0, arr.length - 1);
return Math.max(first, after);
}
// 先手
private static int f(int[] arr, int L, int R) {
if (L == R) {
return arr[L];
}
// 先手拿左侧牌获得的分数
int p1 = arr[L] + g(arr, L + 1, R);
// 先手拿右侧牌获得的分数
int p2 = arr[R] + g(arr, L, R - 1);
return Math.max(p1, p2);
}
// 后手
private static int g(int[] arr, int L, int R) {
if (L == R) {
return 0;
}
// 如果先手拿了左侧牌，后手获得的分数
int p1 = f(arr, L + 1, R);
// 如果先手拿了右侧牌，后手获得的分数
int p2 = f(arr, L, R - 1);
return Math.min(p1, p2);
}
思考上面的递归过程，画出部分递归调用的过程图：
例如，此时纸牌长度下标为 1~5，用 1,5 表示。
- 若拿左侧，还剩下 2~5，用
2,5表示； - 若拿右侧，还剩下 1~4，用
1,4表示；
以此类推，递归调用图中出现了相同的 2,4 ，即出现了 重叠子问题 ，因此就有必要进行 缓存优化 。
这次我们直接根据该递归函数画出最终版本的 动态规划 dp 表。
思路
考虑到递归传递的参数中 f(int[] arr, int L, int R) ，只有 L, R 两个参数会发生变化，且 f 和 g 函数相互依赖。因此，可以构造 两个 以这两个参数为变量 的 二维 dp 数组 。
-
- 思考两个变量的取值范围，构造数组长度。由于
0 ≤ L ≤ R ＜ N，因此将数组长度均设置为 dp[N][N] 。
- 思考两个变量的取值范围，构造数组长度。由于
-
- 由于
L ≤ R， dp 表为上三角矩阵。
- 由于
假设，数组 arr={1, 2, 100, 4}。
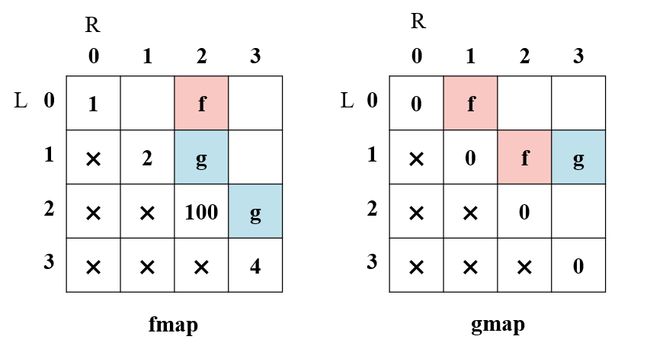
根据递归函数中代码逻辑发现：
- 当为先手时，fmap 的值为：
L == R时为当前 arr[L] 的值。L != R时依赖 gmap 表对应相同位置中arr[L] + gmap(L + 1, R)与arr[R] + gmap(L , R - 1)中的最大值。
这里一定要区分好谁和谁相加后取最大值哦~位置关系别搞乱了！
private static int f(int[] arr, int L, int R) {
if (L == R) {
return arr[L];
}
// 先手拿左侧牌获得的分数
int p1 = arr[L] + g(arr, L + 1, R);
// 先手拿右侧牌获得的分数
int p2 = arr[R] + g(arr, L, R - 1);
return Math.max(p1, p2);
}
- 当为后手时，gmap 的值为：
L == R时为 0 。L != R时依赖 fmap 表对应相同位置中(L + 1, R)与(L , R - 1)中的最小值。
private static int g(int[] arr, int L, int R) {
if (L == R) {
return 0;
}
// 如果先手拿了左侧牌，后手获得的分数
int p1 = f(arr, L + 1, R);
// 如果先手拿了右侧牌，后手获得的分数
int p2 = f(arr, L, R - 1);
return Math.min(p1, p2);
}
由此可以在图中展示出依赖关系：
由此可以完整填出整个 fmap 和 gmap 表：
因此，返回最大值 max(101,6) = 101。
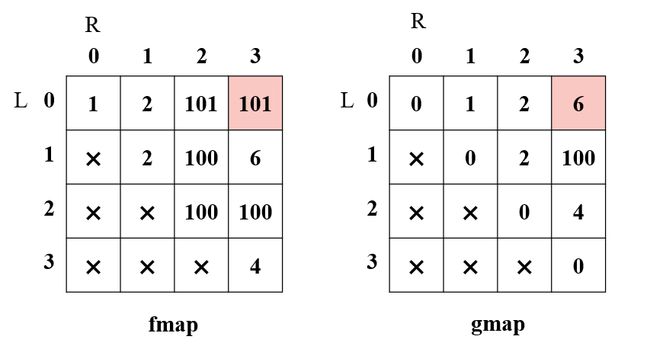
这两张表就是最终动态规划表！
现在我们就通过代码模拟刚才的填表过程：
public static int win(int[] arr) {
if (arr == null || arr.length == 0) {
return 0;
}
int N = arr.length;
int[][] fmap = new int[N][N];
int[][] gmap = new int[N][N];
for (int i = 0; i < N; i++) {
fmap[i][i] = arr[i];
// new 数组时， gmap 本来就为 0
// gmap[i][j] = 0;
}
for (int startCol = 1; startCol < N; startCol++) {
int L = 0;
int R = startCol;
// 从左上到右下斜着填表
while (R < N) { // R 比 L 先到达边界
fmap[L][R] = Math.max(arr[L] + gmap[L + 1][R], arr[R] + gmap[L][R - 1]);
gmap[L][R] = Math.min(fmap[L + 1][R], fmap[L][R - 1]);
// 斜向下走
L++;
R++;
}
}
return Math.max(fmap[0][N - 1], gmap[0][N - 1]);
}
扩展
由于本题的 dp 表是两张 上三角矩阵，因此可以采用 压缩空间 的办法，将 二维数组 矩阵 压缩 为 一维数组 ，可以减少大约一半的矩阵空间，但空间复杂度仍然是 O ( N 2 ) O(N^2) O(N2) 级别的。
这里涉及到了有关 矩阵压缩 的知识，有兴趣的小伙伴可以自行学习下 如何将三角矩阵压缩成为一维数组 哦！
~ 点赞 ~ 关注 ~ 不迷路 ~！！！